モンテカルロ法の基本をわかりやすく説明してみた|マルコフ連鎖モンテカルロ法(MCMC)まで
- モンテカルロ法が全く理解できない…難しすぎる…
- マルコフ連鎖モンテカルロ法とモンテカルロ法って何が違うの??
本記事では、上記の悩みと疑問に答えていきます。
確かに、モンテカルロ法は新しい考え方がたくさんあり、混乱する気持ちはわかります。
そこで、本記事ではモンテカルロ法の基本を確実に理解できるように、具体例を使用して解説しました。
さらに、モンテカルロ法の基本的な考え方からマルコフ連鎖モンテカルロ法までを自然に理解できるように心がけました!
*本記事は、数式のスクロール可能です。
モンテカルロ法の基本知識

一般的に乱数を使用して、その値によって振る舞いが変わるアルゴリズムを『乱択アルゴリズム』といいます。
モンテカルロ法は、乱択アルゴリズムの一つであり、ある確率分布に従う確率変数の平均や分散(統計量)を推定する方法です。
主な特徴は、性質のよくわかっている分布(ガウス分布、一様乱数)だけでなく、離散変数・連続変数からなる様々な確率分布の性質も調べることができる点です。
このことは本記事を読み進めると理解できるので、安心してください!
そうは言っても『乱択アルゴリズムの一つ?』と思う方が多いと思うので、具体例を使って、モンテカルロ法の基本的な考え方を以下で説明していきます。
- モンテカルロ法による期待値評価
- モンテカルロ法のイメージ
- 確率分布からのサンプリング法
乱数(random number)とは、なんらかの確率分布\(p(\mathbf{x})\)に従って生成される値のことです。重要なのは、過去の値に影響を受けずに確率分布から生成されることです。
モンテカルロ法による期待値評価
ある\(P(\mathbf{x})\)に従う\(n\)次元ベクトルの確率変数の期待値は、以下のように定義されます。
定義 : 連続変数・離散変数の期待値
- 連続変数の期待値
$$\mathbb{E}[f(\mathbf{x})] = \int d\mathbf{x} f(\mathbf{x}) P(\mathbf{x})$$
- 離散変数の期待値
$$\mathbb{E}[f(\mathbf{x})] = \sum_{\mathbf{x}} f(\mathbf{x}) P(\mathbf{x})$$
ここで、\(\sum_{\mathbf{x}}\cdots\)は全ての実現値\(\mathbf{x}\)に関する和を取ることを意味します。
仮に\(\mathbf{x} = (x_{1}, x_{2}, \ldots, x_{n})\)の\(X_{i}\)が2種類の離散状態を取る場合、期待値を評価するためには、全ての実現値に関する和(\(2^{n}\)通り)を計算する必要があり、計算量爆発を起こします。
実際に、離散2状態のケースに対して、どのくらいのスピードで全ての実現値の数が増加するのかを以下に示しました。
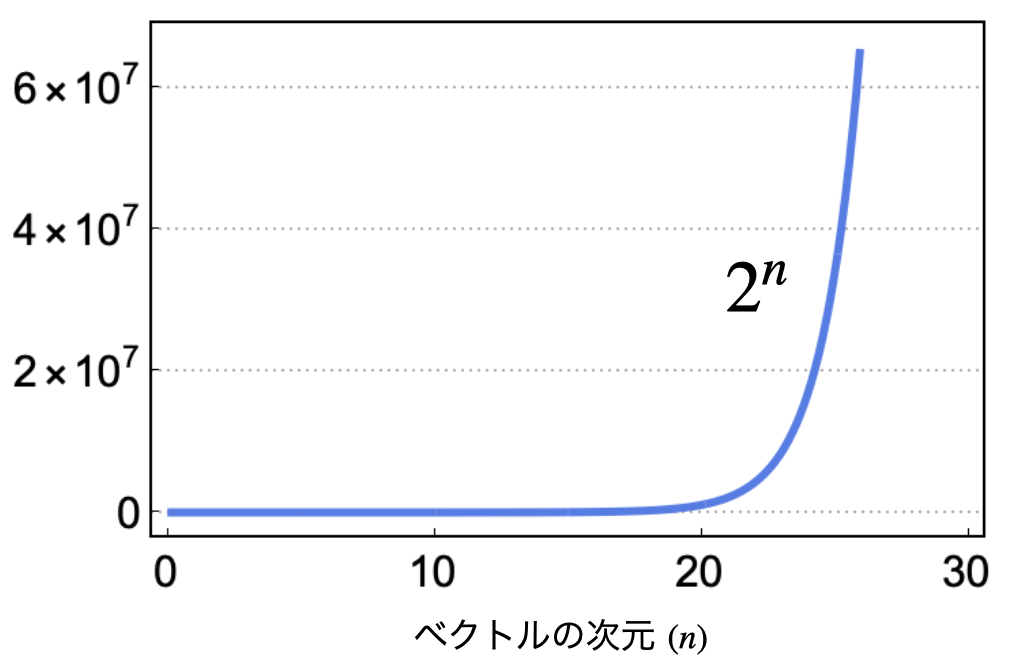 ベクトルの次元と総状態数の関係
ベクトルの次元と総状態数の関係
このように次元が上がるにつれて、全ての実現値の数は、とんでもない数まで増えてしまいます。
連続変数に関しても、仮に\(n\)次元の変数に関する積分を10個のグリットに分けて行う場合、\(10^{n}\)の和を取る必要があります(*ガウス分布のように多重積分が簡単に計算できる場合を除きます)
これらの問題を解決するために、モンテカルロ法のアイデアが有効です!
具体的に、モンテカルロ法のアイデアは以下の通りです。
- 確率分布\(P(\mathbf{x})\)に従うサンプル列\(\{\mathbf{x}\}_{t=1}^{T}\)を生成
- そのサンプルに関する平均(標本平均)により、期待値計算を近似的に評価
具体的には以下のように近似を行います。
モンテカルロ法による期待値評価
$$\mathbb{E}[f(\mathbf{x})] \approx \frac{1}{T} \sum_{t=1}^{T} f(\mathbf{x}^{t})$$
確率論の定理(中心極限定理)から、モンテカルロ法の期待値評価は、サンプル数\(T \to \infty\)の極限で真の期待値に収束します。
また、モンテカルロ法の期待値評価による誤差は、変数の次元に依存せずに減少していきます。
これで、期待値を計算する問題を『確率分布からのサンプリング問題』に変換することができました。
本記事で『サンプリング』と言った場合は、数式で与えられた確率分布から具体的なサンプル(列)を生成することを意味しています。
モンテカルロ法のイメージ
モンテカルロ法は、確率分布\(P(\mathbf{x})\)からサンプル列\(\{\mathbf{x}^{t}\}_{t=1}^{T}\)を生成して、そのサンプル列の平均を取ることで期待値を評価する手法です。
いまいち、イメージが掴めない方もいると思うので、サイコロを例に説明します。
ここで、サイコロは、\(\{1, 2, 3, 4, 5, 6\}\)の目の数を取ることを仮定して、サイコロの出る目(\(X\))の期待値を評価を目指します。
サイコロの例の場合、解析的に期待値を計算でき、計算結果は以下のようになります。
まず、モンテカルロ法を利用して、近似的に出る目の期待値を評価するために、出る目の確率分布(1〜6が出る一様分布)から実際にサンプル列を生成する必要があります。
例えば、1000個のサンプル列を得た場合、以下の式で期待値を近似的に評価するのが、モンテカルロ法のアイデアです。
$$\mathbb{E}[x] \approx \frac{1}{1000} \sum_{t=1}^{1000} x^{t}$$
ここで、各\(x^{i}\)は確率分布からサンプルされた実現値で、サイコロの場合は、1〜6の値になります。
具体的にPythonを用いて、サンプル数とモンテカルロ法によって求めた出る目の期待値の関係を以下に示します。
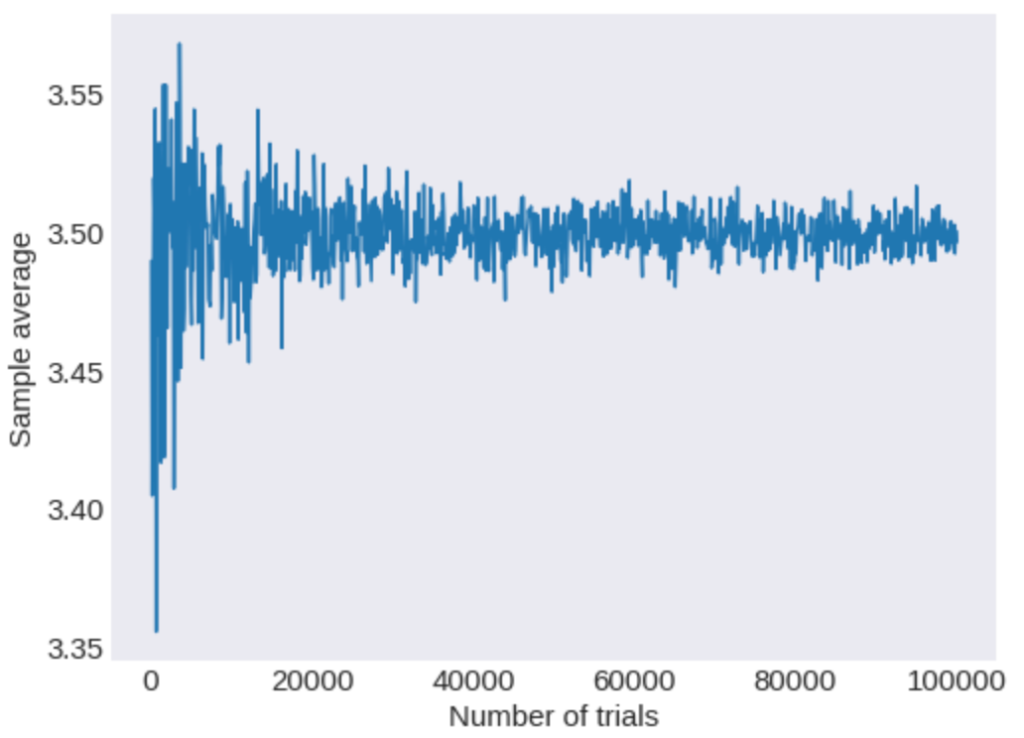 横軸は試行回数(サイコロを振った回数)、縦軸は得られたサンプル列による出た目の平均を意味する。
横軸は試行回数(サイコロを振った回数)、縦軸は得られたサンプル列による出た目の平均を意味する。
試行回数が多くなるにつれて、分散が、小さくなり厳密な期待値である3.5に近づく様子が確認できますね。
サイコロの場合は、一様分布なので簡単に確率分布からのサンプルを得ることができました。
しかし、より複雑な確率分布\(P(\mathbf{x})\)からサンプルを得るためにはどうすれば良いでしょうか?
以降、この疑問に答えていきます。
確率分布からのサンプリング方法
ここまでの話から、十分な数のサンプル列を確率分布\(P(\mathbf{x})\)から得ることできれば期待値を近似的に評価できることがわかりました。
そうは言っても、どのように確率分布からサンプルを生成すれば良いのでしょうか?
モンテカルロ法では、確率分布\(P(\mathbf{x})\)からサンプルを得るために、主に二つの方法が使用されます。
- マルコフ連鎖を用いない方法(静的なモンテカルロ法)
- マルコフ連鎖を用いる方法(マルコフ連鎖モンテカルロ法)
以下では詳しく説明していきます。
マルコフ連鎖を用いない方法(静的なモンテカルロ法)

マルコフ連鎖を用いずに確率分布からサンプリングする方法を『静的なモンテカルロ法』と言います。
具体的には、以下のような方法が主に使用されます。
- 逆関数法
- 棄却サンプリング
- Importance sampling(重点サンプリング)
*Importance samplingは、上記のように独立サンプルを得る方法を指すだけでなく、後述のマルコフ連鎖モンテカルロ法を含むケースがあります(本記事では、独立サンプルを得る方法のことのみ、Importance sampling(重点サンプリング)と呼ぶことにします。)
しかし、高次元の確率分布に対して、静的なモンテカルロ法を適用すると、決定的な問題が生じてしまいます…(本記事最後の参考文献を参考にしてください)
この問題は、後述のマルコフ連鎖モンテカルロ法(MCMC)によって解消されます!
静的なモンテカルロ法にも利点があり、得られるサンプル列は互いに完全に独立となります。
一方、マルコフ連鎖モンテカルロ法により得られるサンプル列は、互いに相関があります。
当ブログでは、静的なモンテカルロ法の理論とPythonによる実装例を紹介しています。
- 逆関数法 : ただいま記事を鋭意製作中です。
- 棄却サンプリング : 【Python】棄却サンプリングの実装と理論
- Importance Sampling(重点サンプリング) : 【Python】重点サンプリング(Importance Sampling)の理論と実装
これらの記事を読めば、高次元で静的なモンテカルロ法が実用的でないことが理解できます!
マルコフ連鎖を用いる方法(マルコフ連鎖モンテカルロ法)

ここからは、マルコフ連鎖モンテカルロ法について説明します。
静的なモンテカルロ法では、高次元の確率分布からサンプルを効率的に得ることは困難となることを説明しました。
マルコフ連鎖モンテカルロ法では、この問題点を解決するために『マルコフ連鎖』と呼ばれる性質を利用します。
当然、『マルコフ連鎖??』という方もいると思うので、マルコフ連鎖から簡単な具体例を用いて説明します。
具体的には、以下の流れで説明していきます。
- マルコフ連鎖とは
- マルコフ連鎖が定常状態となる条件
- マルコフ連鎖の具体例
- マルコフ連鎖モンテカルロ法(MCMC)
- マルコフ連鎖モンテカルロ法(MCMC)の注意点
マルコフ連鎖とは
\(t\)番目の確率変数\(X_{t}\)の条件付き分布が、\(t-1\)番目の確率変数\(X_{t-1}\)の値のみ依存する場合をマルコフ連鎖であると言います。
より形式的には、確率変数の列\(\{\mathbf{x}^{1}, \ldots,\mathbf{x}^{t}, \ldots \}\)が以下を満たしている場合、マルコフ連鎖と言います。
$$P(\mathbf{x}^{t+1} \mid \mathbf{x}^{t}, \ldots, \mathbf{x}^{1}) = P(\mathbf{x}^{t+1} \mid \mathbf{x}^{t})$$
\(\mathbf{x}^{t}\)のとりうる値の集合\(\mathcal{S}\)は、一般的に状態空間と呼ばれます。
また、\(P(\mathbf{x}^{t+1} \mid \mathbf{x}^{t})\)を遷移確率といい\(W(\mathbf{x}^{t+1} \mid \mathbf{x}^{t}) \equiv P(\mathbf{x}^{t+1} \mid \mathbf{x}^{t}) \)と表すことにします(今回は、遷移確率が時間に依存しない場合を考えます)
- 表記に関して : 論文や教科書によっては、\(T(\mathbf{x}^{t+1} \mid \mathbf{x}^{t})\)と書くこともあり、特に統一した表記はないと思います…
- 用語
- 確率変数列 \((X_{0}, \ldots, X_{M})\)の同時分布からのサンプル\((x_{0}, \ldots, x_{M})\)を経路という。
マルコフ連鎖の性質から、遷移確率を利用して、確率分布の時間発展を次のように記述することができます。
$$P_{t+1}(\mathbf{x}) = \sum_{\mathbf{x}^{\prime}} W(\mathbf{x} \mid \mathbf{x}^{\prime}) P_{t}(\mathbf{x}^{\prime})$$
一般にこの方程式は『(離散)マスター方程式』と呼ばれています。
また、遷移確率は以下の確率の条件を満たします。
遷移確率の条件
任意の状態\(\mathbf{x} \in \mathcal{S}\)に対して以下が成り立つ。
- \(W(\mathbf{x}^{\prime} \mid \mathbf{x}) \ge 0\)
- \(\sum_{\mathbf{x}} W(\mathbf{x} \mid \mathbf{x}^{\prime}) = 1 \)
マルコフ連鎖が定常分布をもつ条件
マルコフ連鎖は、\(t \to \infty\)とすると初期状態に依存せず、一定の確率分布に収束する場合があります。
一般に収束した分布のことを『定常分布(または不変分布)』といいます。
より形式的には、以下の条件を満たすような確率分布を定常分布(または、不変分布)といいます。
定常状態
$$P_{\infty}(\mathbf{x}) = \sum_{\mathbf{x}^{\prime}} W(\mathbf{x} \mid \mathbf{x}^{\prime}) P_{\infty}(\mathbf{x}^{\prime})$$
すなわち、\(t \to \infty\)の場合、遷移の前後で確率分布が変化しない状態のことです。
このような状態に到達するためには、遷移確率は次の三つの必要十分条件を満たす必要があります。
定常状態に到達する遷移確率の条件
- 規約性 : 任意の二つの状態\(\mathbf{x}, \mathbf{x}^{\prime}\)が有限のステップで遷移可能
- 非周期性 : ある状態\(\mathbf{x}\)から\(\mathbf{x}\)に戻ってくるまでステップ数の最大公約数が周期に対応し、その値が\(1\)のとき周期がないことを意味し、任意の\(\mathbf{x}\)に対して周期が\(1\)のことを非周期性をもつという
- 状態数が有限である
この三つの条件を満たせば、初期条件に依存しない唯一の定常分布が存在することが示せます。
この三つの性質を満たすとき、エルゴード性をもつといいます。
マルコフ連鎖の具体例
マルコフ連鎖モンテカルロ法の説明に入る前に、定常分布に収束するようなマルコフ連鎖の具体例を紹介します。
一般に、状態空間\(\mathcal{S}\)を頂点で表し、遷移確率をエッジで表したものを状態遷移図といいます。
具体的な状態空間として(晴れ、くもり、雨)のケースを考え、遷移確率を以下の状態遷移図で与えた場合を考えてみましょう。
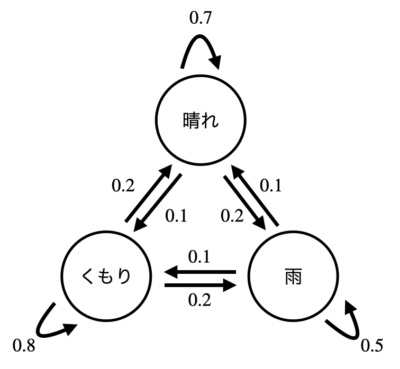 マルコフ連鎖の具体例、エッジ上の数字は遷移確率を表します。
マルコフ連鎖の具体例、エッジ上の数字は遷移確率を表します。
このとき、最初に確率1で晴れとなる状態からスタートしたマルコフ連鎖は、以下のようになります。
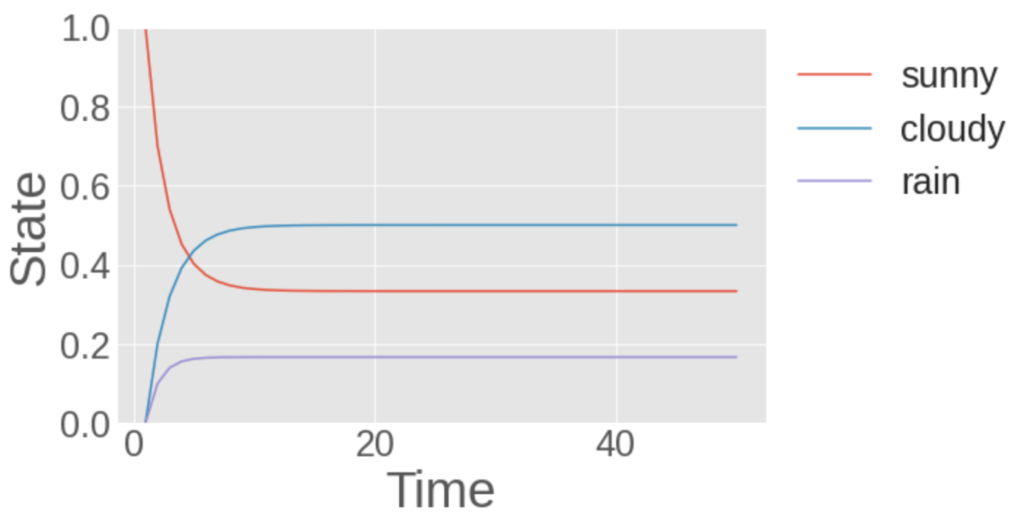 初期条件として晴れになる確率を1として行ったシミュレーション。縦軸は状態のとりうる確率を表し、横軸は状態遷移の回数を表します。
初期条件として晴れになる確率を1として行ったシミュレーション。縦軸は状態のとりうる確率を表し、横軸は状態遷移の回数を表します。
次に初期条件として、雨になりうる確率が1となる状態から始めた例を示します。
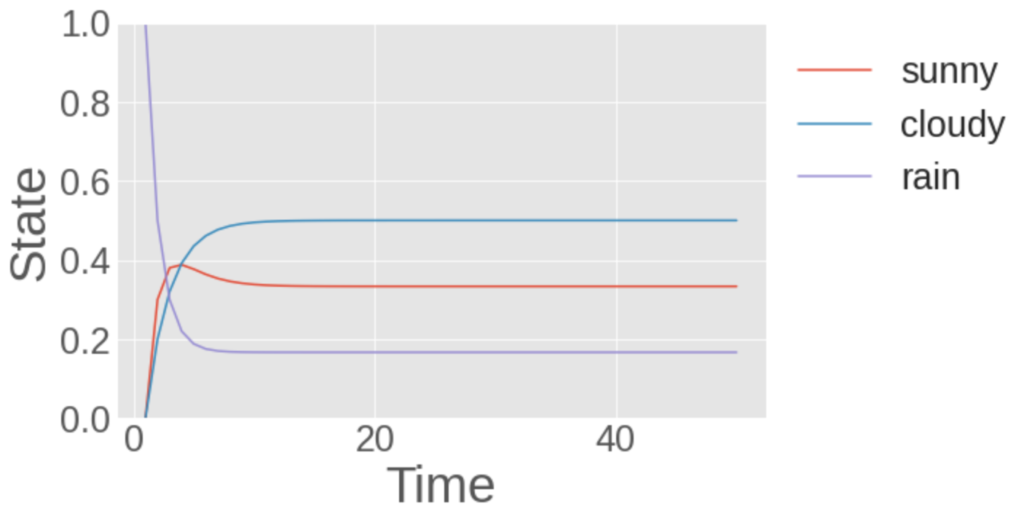 初期条件として雨になる確率を1として行ったシミュレーション。縦軸は状態のとりうる確率を表し、横軸は状態遷移の回数を表します。
初期条件として雨になる確率を1として行ったシミュレーション。縦軸は状態のとりうる確率を表し、横軸は状態遷移の回数を表します。
このように異なる初期値から始めても、最終的には、同じ状態に収束することが確認できます。
まさに、定常分布に収束している状態です!!
下記にシミュレーションに使用したコード(Python)を共有します。
def mc(x0=[[1.0], [0.0], [0.0]], times=100):
'''
INPUT
x0 : 初期条件
times : 状態の更新回数
OUTPUT
state : マルコフ連鎖のサンプル列
'''
x = np.array(x0)
state = np.zeros((times, 3))
state[0] = x.ravel()
for i in range(times-1):
x = trans_prob@x
state[i+1] = x.ravel()
return state
適当な初期値から始めて皆さんも遊んでみてください。
また、今回の定常分布の具体的な形式は、定常分布の定義を使うと簡単に導くことができるので挑戦してみてください。
マルコフ連鎖モンテカルロ法(MCMC)
マルコフ連鎖モンテカルロ法(MCMC)のアイデアは、以下の通りです。
サンプリングしたい確率分布\(P(\mathbf{x})\)が定常状態となるようなマルコフ連鎖を構築すれば、マルコフ連鎖を利用してサンプリングができるぞ!
実際にそのようなマルコフ連鎖を構成することは可能で、遷移確率が以下の条件を満たすとき、定常分布はサンプリングしたい確率分布\(P(\mathbf{x})\)になります。
サンプルしたい確率分布が定常分布となるための遷移確率の条件
- つりあい条件 : 任意の状態\(\mathbf{x}\)に対して確率の流入と流出の合計が等しい。すなわち以下を満たす。
- エルゴード性
- 非周期性(ラフにいうと、状態が周期を持たないことです)
ここまでくれば、あとは、『つりあい条件を満たすような遷移確率を構築すれば良いだけだ!!』と思いますが、条件数が少なくて、どのように遷移確率を構築するべきかは自明ではありません…
そこで、つりあい条件よりも強い条件となる以下の『詳細つりあい条件』を満たすように遷移確率を構築する方法が使用されます。
詳細つりあい条件
任意の\(\mathbf{x}, \mathbf{x}^{\prime} \in \mathcal{S}\)に関して以下が成り立つ。
$$ W(\mathbf{x} \mid \mathbf{x}^{\prime}) P(\mathbf{x}^{\prime}) = W(\mathbf{x}^{\prime} \mid \mathbf{x}) P(\mathbf{x}) $$
詳細つりあい条件を満たすような遷移確率により生成されるマルコフ連鎖は、可逆と呼ばれます。
詳細つりあい条件を満たすような遷移確率を構成することは簡単ですが、つりあい条件を満たすが詳細つりあい条件を満たさない例を作ることは大変です(挑戦してみてください!)
一応確認ですが、詳細つりあい条件を用いると、確率分布\(P(\mathbf{x})\)が定常分布の条件を満たすことが以下のように導けます。
\begin{align} \sum_{\mathbf{x}} P(\mathbf{x}) W(\mathbf{x}^{\prime} \mid \mathbf{x}) &\overset{(a)}{=} \sum_{\mathbf{x}} P(\mathbf{x}^{\prime}) W(\mathbf{x} \mid \mathbf{x}^{\prime}) \\ &\overset{(b)}{=} P(\mathbf{x}^{\prime}) \sum_{\mathbf{x}} W(\mathbf{x} \mid \mathbf{x}^{\prime}) \\ &\overset{(c)}{=} P(\mathbf{x}^{\prime}) \end{align}
式変形について
(a) : 詳細つりあい条件を使用
(b) : \(\sum_{\mathbf{x}} \cdots \)なので\(P(\mathbf{x}^{\prime})\)は総和の外に出せる
(c) : 確率の保存(\(\sum_{\mathbf{x}}W(\mathbf{x} \mid \mathbf{x}^{\prime}) =1 \))を使用
つりあい条件を満たすと定常状態が存在することが保証されることの証明には、『ペロン-フロベニウスの定理』と呼ばれる性質を使用します。
また、遷移確率行列の第二固有値によって定常状態に到達するまでの時間が深く関わっていることも示せます。
遷移確率の種類|詳細つりあいを満たす場合

ここからは、詳細つりあい条件を満たすマルコフ連鎖モンテカルロ法の例を紹介します。
具体的には、以下の4つを説明します。
- メトロポリス法
- メトロポリス・ヘイスティング法
- ギブスサンプリング(熱浴法)
- ハイブリッドモンテカルロ法(or ハミルトニアンモンテカルロ法)
以下、詳しく説明します。
メトロポリス法
メトロポリス法は、遷移確率を提案分布\(C(\mathbf{x}^{\prime} \mid \mathbf{x})\)と受理確率\(A(\mathbf{x}, \mathbf{x}^{\prime})\)に分けて考えます。
そして、遷移確率を以下のように構成します。
ここで、提案分布は、\(C(\mathbf{x}^{\prime} \mid \mathbf{x}) = C(\mathbf{x} \mid \mathbf{x}^{\prime})\)となるものを使用します。
すなわち、この遷移確率は提案した先の\(\mathbf{x}^{\prime}\)の確率密度関数\(P(\mathbf{x}^{\prime}\)が提案前の確率密度関数\(P(\mathbf{x})\)より大きければ必ず遷移させ、小さい場合は\(P(\mathbf{x}^{\prime}) / p(\mathbf{x})\)の確率で遷移させることを意味します。
また、この遷移確率は、\(P(\mathbf{x}^{\prime}) / P(\mathbf{x})\)の形で表せるため、元の確率密度関数\(P(\mathbf{x})\)の規格化定数が未知でもメトロポリス法は適用できます!
MCMCを使用することが多い以下のエネルギーベースモデルの例でご利益を一応確認しておきましょう。
$$P(\mathbf{x}) = \frac{1}{Z(\beta)} e^{- \beta E(\mathbf{x})}$$
ここで、\(\beta\)は逆温度と呼ばれるパラメータで、\(Z(\beta)\)は規格化定数で\(Z(\beta) = \sum_{\mathbf{x}} e^{- \beta E(\mathbf{x})}\)と計算されます。
一般に、エネルギーベースモデルでは、規格化定数の計算が困難となることが多いです。しかし、メトロポリス法の遷移確率は規格化定数の計算無しで次のように計算できます。
$$W(\mathbf{x}^{\prime} \mid \mathbf{x}) = C(\mathbf{x}^{\prime} \mid \mathbf{x}) \min \left(1, e^{-\beta(E(\mathbf{x}^{\prime}) – E(\mathbf{x}) )} \right)$$
メトロポリス法が詳細つりあい条件を満たすことを証明
メトロポリス法が詳細つりあい条件を満たすことを確認します。
任意の二つの状態\(\mathbf{x}\), \(\mathbf{x}^{\prime}\)に対して、一般性を失わないように\(P(\mathbf{x}^{\prime}) \le P(\mathbf{x})\)を仮定します。
すると、状態\(\mathbf{x} \to \mathbf{x}^{\prime}\)の遷移確率は、\(P(\mathbf{x}^{\prime}) \le P(\mathbf{x})\)より以下のようになります。
$$W(\mathbf{x}^{\prime} \mid \mathbf{x}) = C(\mathbf{x}^{\prime} \mid \mathbf{x}) \frac{P(\mathbf{x}^{\prime})}{P(\mathbf{x})}$$
一方、状態\(\mathbf{x}^{\prime} \to \mathbf{x}\)の遷移確率は、以下のようになります。
$$W(\mathbf{x} \mid \mathbf{x}^{\prime}) = C(\mathbf{x} \mid \mathbf{x}^{\prime})$$
この結果より、以下のように変形できます。
また、\(C(\mathbf{x}^{\prime} \mid \mathbf{x}) = C(\mathbf{x} \mid \mathbf{x}^{\prime}) \)より、以下の詳細つりあい条件を満たします。
$$P(\mathbf{x}) W(\mathbf{x}^{\prime} \mid \mathbf{x}) = P(\mathbf{x}^{\prime}) W(\mathbf{x} \mid \mathbf{x}^{\prime})$$
提案分布\(C(\mathbf{x} \mid \mathbf{x})\)はカスタマイズ可能で提案の仕方次第で性能は大きく変わります。
メトロポリス・ヘイスティング法(MH法)
メトロポリス・ヘイスティング法(MH法)は、提案分布が\(C(\mathbf{x}^{\prime} \mid \mathbf{x}) \neq C(\mathbf{x} \mid \mathbf{x}^{\prime}) \)を満たさないケースにも適応できるようにメトロポリス法を一般化した方法です。
一般化と行っても簡単で受理確率を以下のように定義するだけです。
$$A(\mathbf{x}, \mathbf{x}^{\prime}) \equiv \min \left(1, \frac{P(\mathbf{x}^{\prime})C(\mathbf{x} \mid \mathbf{x}^{\prime})}{P(\mathbf{x})C(\mathbf{x}^{\prime} \mid \mathbf{x})} \right)$$
メトロポリス法と同じ流れで詳細つりあい条件が成り立つことを示すことができます。
今回も任意の二つの状態\(\mathbf{x}\), \(\mathbf{x}^{\prime}\)に対して、一般性を失わないように\(P(\mathbf{x}^{\prime}) \le P(\mathbf{x})\)を仮定します。
すると、状態\(\mathbf{x} \to \mathbf{x}^{\prime}\)の遷移確率は、\(P(\mathbf{x}^{\prime}) \le P(\mathbf{x})\)より以下のようになります。
一方、状態\(\mathbf{x}^{\prime} \to \mathbf{x}\)の遷移確率は、以下のようになります。
$$W(\mathbf{x} \mid \mathbf{x}^{\prime}) = C(\mathbf{x} \mid \mathbf{x}^{\prime})$$
ゆえに、以下の詳細つりあい条件が成り立ちます。
$$P(\mathbf{x}) W(\mathbf{x}^{\prime} \mid \mathbf{x}) = P(\mathbf{x}^{\prime}) W(\mathbf{x} \mid \mathbf{x}^{\prime} )$$
\(\mathbf{x}\)に依存しない提案分布を使用する方法を独立サンプラーと言います。
この場合受理確率は、以下のようになります。
$$A(\mathbf{x}, \mathbf{x}^{\prime}) = \min \left(1, \frac{P(\mathbf{x}^{\prime})C(\mathbf{x})}{P(\mathbf{x})C(\mathbf{x}^{\prime})} \right)$$
提案分布が以前の状態に依存しないため受理されたサンプル同士は独立になります。
しかし、\(C(\mathbf{x})\)と\(P(\mathbf{x})\)が十分似ていないと受理確率は小さくなってしまい、サンプルを得ることは難しくなります。
ギブスサンプリング(熱浴法)
ギブスサンプリングは、MH法の提案分布\(C(\mathbf{x} \mid \mathbf{x}^{\prime})\)として、\(\mathbf{x} = (x_{1}, \ldots, x_{n})\)のうち一つの状態を選び、各状態\(x_{i}\)が以下の確率で与えられるように提案します。
\begin{align}W((x_{i}^{\prime}, \mathbf{x}_{-i}) \mid (x_{i}, \mathbf{x}_{-i})) &= P(x_{i}^{\prime} \mid \mathbf{x}_{-i}) \\ W((x_{i}, \mathbf{x}_{-i}) \mid (x^{\prime}_{i}, \mathbf{x}_{-i})) &= P(x_{i} \mid \mathbf{x}_{-i})\end{align}
ここで、表記を簡単にするために\(\mathbf{x} = (x_{1}, \ldots)\)から\(i\)番目の要素を抜き取った状態を\(\mathbf{x}_{-i}\)と表しました。
すると受理確率は以下のように1になります。
\(\mathbf{x}^{\prime}\)が\(\mathbf{x}\)に関係せずに遷移するのでサンプル間の相関を減らすことが期待されます!
しかし、ギブスサンプリングを使用する場合、条件付き確率が計算できることが必須です。
これを繰り返すことで、サンプルしたい確率分布を定常状態とするマルコフ連鎖を構築することができます。
また、置き換える成分の番号\(i\)はランダムに選んでも、規則的に選んでも良いです。
Hybrid Monte Calro法
Hybrid Monte Calro法(HMC法)は、メトロポリス法と分子動力学という二つの異なる方法を組み合わせたモンテカルロ法です。
少し複雑なので今回は説明を省略します。
マルコフ連鎖モンテカルロ法(MCMC)の注意点
マルコフ連鎖モンテカルロ法の注意点は以下の二つです。
- マルコフ連鎖の最初の数ステップは、初期値\(\mathbf{x}^{0}\)と相関をもち定常分布からのサンプルになっていない
- \(\mathbf{x}^{t}\)を変化させて\(\mathbf{x}^{t+1}\)を作るため\(\mathbf{x}^{t}\)と\(\mathbf{x}^{t+1}\)に相関が生じる(自己相関)
①の対処法としては、マルコフ連鎖の最初の数ステップを期待値近似のためのサンプル列に含まないようにすることで初期状態の相関を無くします。
初期状態の相関が消える目安となる時間を『マルコフ連鎖の混合時間(または緩和時間)』といい、最初の数ステップのサンプル列を捨てることを『バーンイン』といいます。
②の対処法としては、各サンプルが独立になるように自己相関がなくなるくらいの間隔を空けて、期待値近似のためのサンプル列を取得します。
この自己相関がなくなるくらいの間隔は、ある程度定量的に評価することができます(ジャックナイフ法と呼ばれる手法を使用したりします)
しかし、やや複雑なので本記事では省略します。
または、異なる初期値から独立に複数のマルコフ連鎖を走らせて、各マルコフ連鎖からサンプルを得るという方法も使用されます。
この場合、得られるサンプル同士は完全に独立になります。
MCMCを効率化する方法
MCMCを効率化するためには、自己相関が早く減衰するような遷移確率を構築する必要があります。
そのためには、モデルに内在する知識を利用して、クラスター単位で提案を行うような手法があります。
細かい説明はしませんが、よく使用される手法を三つ紹介します。
- Swendsen-Wang アルゴリズム
- Wolffアルゴリズム
- ループアルゴリズム
他にも詳細つりあいを満たさない遷移確率を構築したり、拡張した確率分布を考え、効率化する交換モンテカルロ法と呼ばれる手法もあります。
マルコフ連鎖モンテカルロ法の実装例
当ブログでは、マルコフ連鎖モンテカルロ法の理解を深めるために主にガウス分布を使用した適用例を紹介しています。
*全ての実装はPythonを利用しています。
メトロポリス法の実装例
混合ガウス分布を用いたPythonによる実装例を紹介しています。
ギブスサンプリングの実装例
条件付き確率が計算できる二変量ガウス分布を具体例として、Pythonによる実装を紹介しています。
実装のみならず、導入部分でガウス分布の簡単な説明を行なっているのでぜひ参考にしてください。

マルコフ連鎖モンテカルロ法の応用例
当ブログでは、例題を使用し、マルコフ連鎖モンテカルロ法の応用例を紹介し、Pythonによる実装を共有しています。
その例を簡単に紹介します。
統計物理学のイジングモデルへの応用
実は、マルコフ連鎖モンテカルロ法は、イジングモデルと呼ばれる磁性体の性質を調べるために開発された手法といわれています。
その理論と具体例は下記を参考にしてください。
参考資料

本記事作成と私が勉強するために使用した資料を説明していきます。
【学生限定】専門書等をAmazonを経由して購入する場合は、『Prime Student』の利用をおすすめします(大学院生も可能)
全てのメリットは書ききれませんが、私が思う最大のメリットは以下の7つです。
- 6ヶ月間無料で使用できる
- 登録が2〜3分で完了する
- 書籍が最大10%割引
- 文房具が最大20%割引
このサービスは在学期間(登録してから最大4年)のみ使用可能です。
私は、『Prime Student』を大学3年次に知り深く後悔したのを覚えています…(というか怒りすら感じていました)
あくまで参考ですが、より詳しいメリットと登録方法に関しては、下記を参考にしてください。
参考文献
参考文献を紹介します。
計算統計 II-マルコフ連鎖モンテカルロ法とその周辺 (統計科学のフロンティア)
理論から実装上の注意点がまとまっています。
マルコフ連鎖モンテカルロ法を研究する際は必ず読むべき一冊です。
ゼロからできるMCMC マルコフ連鎖モンテカルロ法の実践的入門 (KS理工学専門書)
実際にプログラミングによる実装と説明がよくまとまっています。
やさしいMCMC入門: 有限マルコフ連鎖とアルゴリズム
決してやさしくはなく理論もしっかり説明されています。
参考URL
参考にした資料に関するURLを下記にまとめます。
参考にしたYouTube講義は以下の講義です。
参考オンデマンド講義
Udemyの下記の講義もPythonによる実装と理論を理解するのに有益でした。
ベイズ統計の文脈で具体的にマルコフ連鎖モンテカルロ法を利用するので、実務で使用したい方必見の講義です。
まとめ
モンテカルロ法の基礎を簡単にまとめました。
皆さんも理解したら一度立ち止まり、式を追ってみたり、実際に実装してみたりして、理解をより深く定着させてください。
また、モンテカルロ法は、確率統計理論の性質に基づき期待値評価の正当性が評価されます。
そのため、確率統計の性質を理解することで、モンテカルロ法の理解をさらに深めることができます。
もし、確率統計の勉強に興味がある方は下記の参考書を参考にしてください。

また、ベイズ統計をはじめ、機械学習の文脈でもマルコフ連鎖モンテカルロ法はよく使用されます。
例えば、データの背後にある確率分布を近似的に表現する生成モデル等でも頻繁に使用されます(下記参照)


Pythonを学習するのに効率的なサービスを紹介していきます。
まず最初におすすめするのは、Udemyです。
Udemyは、Pythonに特化した授業がたくさんあり、どの授業も良質です。
また、セール中は1500円定義で利用することができ、コスパも最強です。
下記の記事では、実際に私が15個以上の講義を受講して特におすすめだった講義を紹介しています。

他のPythonに特化したオンライン・オフラインスクールも下記の記事でまとめています。

自分の学習スタイルに合わせて最適なものを選びましょう。
また、私がPythonを学ぶ際に使用した本を全て暴露しているので参考にしてください。