【Python】ギブスサンプリングの応用(多変量ガウス分布)
本記事では、マルコフ連鎖モンテカルロ法の一つであるギブスサンプリン(Gibbs Sampling)をガウス分布に適用した具体例をPythonを使用し実装しました。
マルコフ連鎖モンテカルロ法の基本を理解していない方は先に下記の記事を参考してから本記事で実装を楽しんでください。

多変量ガウス分布の基本

今回は、モンテカルロ法の具体例として、他変量ガウス分布を扱っていきます。
\(\vec{x} \in \mathbb{R}^{n}\)に対する多変量ガウス分布は以下のように表せます。
$$p(\vec{x} \mid \vec{\mu}, \Sigma) = \frac{1}{\sqrt{(2 \pi)^{n} |\Sigma|}} \exp \left(- \frac{1}{2} (\vec{x} – \vec{\mu})^{\top} \Sigma^{-1} (\vec{x} – \vec{\mu}) \right)$$
ここで、\(\vec{\mu}\)と\(\Sigma\)はそれぞれ平均ベクトルと分散共分散行列を表します。
今回は、具体例として一番簡単な2変数のガウス分布のケースを扱います。
2変数ガウス分布
2変数ガウス分布は、2変数\(\vec{x} \equiv (x, y)^{\top}\)に対して以下のように表すことができます。
$$p(\vec{x} \mid \vec{\mu}, \Sigma) = \frac{1}{\sqrt{(2 \pi)^{2} |\Sigma|}} \exp \left(- \frac{1}{2} (\vec{x} – \vec{\mu})^{\top} \Sigma^{-1} (\vec{x} – \vec{\mu}) \right)$$
ここで、\(\vec{\mu}\)と\(\Sigma\)は以下のように定義しました。
$$\vec{\mu} = \left(\begin{array}{c} \mu_{x} \\ \mu_{y} \end{array} \right)$$
$$\Sigma = \left(\begin{array}{cc} \sigma_{xx}^{2} & \rho \sigma_{xx} \sigma_{yy} \\ \rho \sigma_{xx} \sigma_{yy} & \sigma_{yy}^{2} \end{array} \right)$$
ここで、\(\rho\)は相関係数を表します。
以降、この2変数ガウス分布からモンテカルロ法を使用してサンプリングを行う方法を紹介します。
ギブスサンプリングの具体例(2変数ガウス分布)

ギブスサンプリングを実行するためには、サンプリングを行う分布の条件付き分布が必要でした。
2変数ガウス分布の場合、各変数の条件付き確率を計算することができ、以下のように表せます。
$$p(x \mid y) = \mathcal{N}\left(\mu_{x} + \rho\frac{\sigma_{xx}}{\sigma_{yy}}(y – \mu_{y}), \sigma_{xx}^{2}(1 – \rho^{2}) \right)$$
$$p(y \mid x) = \mathcal{N}\left(\mu_{y} + \rho\frac{\sigma_{yy}}{\sigma_{xx}}(x – \mu_{x}), \sigma_{yy}^{2}(1 – \rho^{2}) \right)$$
この二つの条件付き確率はガウス分布なので簡単にサンプリングできます。
この結果を使うとギブスサンプリングのアルゴリズムは以下のようになります。
ギブスサンプリング(2変数ガウス分布)
- 適当に初期状態\(x^{0}, y^{0}\)を設定
- 以下を繰り返す
- 新しい\(x\)を\(p(x \mid y)\)で選ぶ
- 新しい\(y\)を\(p(y \mid x)\)で選ぶ
ギブスサンプリングの実装

ここからは、ギブスサンプリングのPythonによる実装を紹介します。
まずは、使用するライブラリをインストールしてください。
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(0)
from scipy import stats
2変数ガウス分布をプロット
サンプリングを行う2変数ガウス分布をプロットします。
mu_x, mu_y = 0.0, 0.0
sigma_x, sigma_y = 1.0, 1.0
rho = 0.5
# 平均
mus = np.array([mu_x, mu_y])
# 分散共分散行列
sigmas = np.array([[sigma_x**2, rho*sigma_x*sigma_y],
[rho*sigma_x*sigma_y, sigma_y**2]])
x = np.arange(-5.0, 5.0, 0.1)
y = np.arange(-5.0, 5.0, 0.1)
X, Y = np.meshgrid(x, y)
pos = np.dstack((X, Y))
Z = stats.multivariate_normal.pdf(pos, mean=mus, cov=sigmas)
fig, ax = plt.subplots(figsize=(12, 9))
cntr = ax.contour(X, Y, Z)
ax.clabel(cntr, fontsize=15)
plt.tick_params(axis='y', labelsize=20)
plt.tick_params(axis='x', labelsize=20)
plt.figure()
<output>
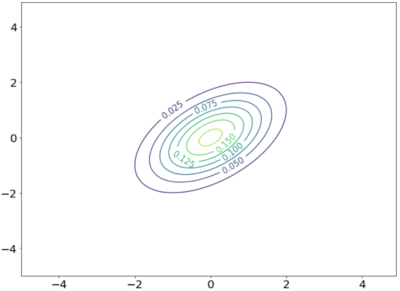 2変数ガウス分布の等高線
2変数ガウス分布の等高線
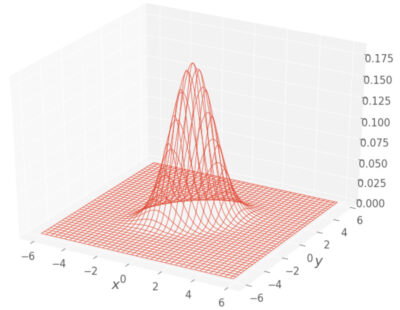
3次元プロットで図示すると以下のような感じです。
x = np.arange(-6.0, 6.0, 0.1)
y = np.arange(-6.0, 6.0, 0.1)
X, Y = np.meshgrid(x, y)
pos = np.dstack((X, Y))
Z = stats.multivariate_normal.pdf(pos, mean=mus, cov=sigmas)
fig, ax = plt.subplots(figsize=(12, 9), subplot_kw={'projection' : '3d'})
surface = ax.plot_wireframe(X, Y, Z, linewidth=0.8)
ax.set_xlabel(r'$x$', fontsize=20)
ax.set_ylabel(r'$y$', fontsize=20)
plt.tick_params(axis='y', labelsize=15)
plt.tick_params(axis='x', labelsize=15)
plt.tick_params(axis='z', labelsize=15)
plt.show()
<output>
ギブスサンプリングの実装
まずは、以下のように条件付き確率を定義します。
# p(x|y)
def px_cond_y(y):
px_mean = mu_x + rho*(sigma_x/sigma_y)*(y-mu_y)
px_scale = sigma_x*np.sqrt(1-rho**2)
return np.random.normal(loc=px_mean, scale=px_scale)
# p(y|x)
def py_cond_x(x):
py_mean = mu_y + rho*(sigma_y/sigma_x)*(x-mu_x)
py_scale = sigma_y*np.sqrt(1-rho**2)
return np.random.normal(loc=py_mean, scale=py_scale)
次に前半分布で説明したギブスサンプリングのアルゴリズムを実装します。
def gibbs_sampling(steps=1000, x_init=[0, 0]):
'''Gibbs Sampling
Parameters
steps : モンテカルロステップ数
x_init : 初期状態
Return
samples : Gibbs Samplingの結果
'''
samples = [x_init]
x, y = x_init[0], x_init[1]
for i in range(steps):
x = px_cond_y(y)
samples.append([x, y])
y = py_cond_x(x)
samples.append([x, y])
return np.array(samples)
これでギブスサンプリングの実装は終了です。
ギブスサンプリングの結果
ギブスサンプリングの実装結果を紹介します。
# 初期条件
x_init = [-4.0, -4.0]
# ギブスサンプリングの実行
samples = gibbs_sampling(steps=1000, x_init=x_init)
fig, ax = plt.subplots(figsize=(12, 9))
ax.scatter(samples[:, 0], samples[:, 1], alpha=0.15, c='g')
ax.plot(samples[:50, 0], samples[:50, 1], c='r')
ax.plot(x_init[0], x_init[1], marker='.', ms=15, c='k')
cntr = ax.contour(X, Y, Z)
ax.clabel(cntr, fontsize=15)
ax.annotate('Initial Condition', xy=(x_init[0]-0.5, x_init[1]-0.5), fontsize=18)
plt.legend(fontsize=17)
plt.tick_params(axis='y', labelsize=20)
plt.tick_params(axis='x', labelsize=20)
plt.figure()
<output>
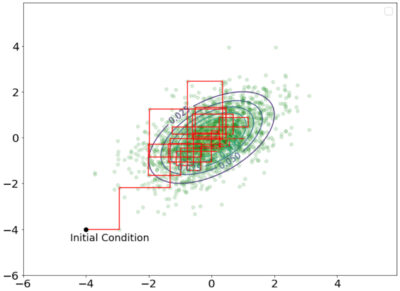 ギブスサンプリンの実行。黒点は初期状態を表し、赤線はマルコフ連鎖の最初の50ステップを可視化した。
ギブスサンプリンの実行。黒点は初期状態を表し、赤線はマルコフ連鎖の最初の50ステップを可視化した。
実際にサンプリングが成功しているかを確認するために3次元ヒストグラムを作成してみました。
x = np.arange(-6.0, 6.0, 0.1)
y = np.arange(-6.0, 6.0, 0.1)
X, Y = np.meshgrid(x, y)
pos = np.dstack((X, Y))
Z = stats.multivariate_normal.pdf(pos, mean=mus, cov=sigmas)
# 初期状態
x_init = [-4.0, -4.0]
# ギブスサンプリング
samples = gibbs_sampling(steps=10000, x_init=x_init)
hist, x_edges, y_edges = np.histogram2d(samples[:, 0], samples[:, 1], bins=30, density=True)
X_hist, Y_hist = np.meshgrid(x_edges[:-1], y_edges[:-1])
Z_hist = 0
dx = X_hist[0, 1] - X_hist[0, 0]
dy = Y_hist[1, 0] - Y_hist[0, 0]
dz = hist.ravel()
X_hist = X_hist.ravel()
Y_hist = Y_hist.ravel()
fig, ax = plt.subplots(figsize=(12, 9), subplot_kw={'projection' : '3d'})
surface = ax.plot_wireframe(X, Y, Z, linewidth=1.5, alpha=0.8)
ax.bar3d(X_hist, Y_hist, Z_hist, dx, dy, dz, alpha=0.4, color='c')
plt.tick_params(axis='y', labelsize=15)
plt.tick_params(axis='x', labelsize=15)
plt.tick_params(axis='z', labelsize=15)
ax.set_xlabel(r'$x$', fontsize=20)
ax.set_ylabel(r'$y$', fontsize=20)
plt.show()
<output>
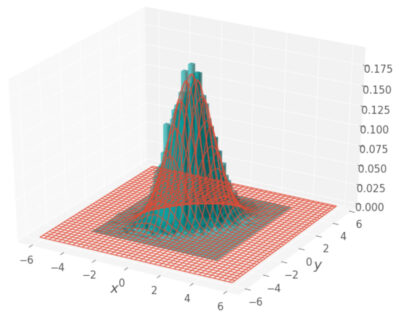 ギブスサンプリングの結果を3次元ヒストグラムで可視化
ギブスサンプリングの結果を3次元ヒストグラムで可視化
しっかりと、二変量ガウス分布からサンプリングができていることが確認できました。
まとめ
本記事では、マルコフ連鎖モンテカルロ法の一つであるギブスサンプリンを二変量ガウス分布を例に実装してみました。

『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。