本記事では、マルコフ連鎖モンテカルロ法の具体例として、物理学で有名なイジング模型と呼ばれる模型のシミュレーションを行います。
近年、イジング模型は量子計算や最適化計算にも応用され注目を浴びています。
そのため、本記事で紹介するイジング模型の基本概念やシミュレーション実習は皆さんの視野を広げること間違いなしです(少し言い過ぎかも)
*追加事項を随時更新します(間違いやコメントがあったら私のTwitterに連絡してください)
イジング模型の基礎知識

まずは、イジング模型(強磁性イジング模型)の基礎知識を以下の流れで説明します。
- エネルギーベースモデル(Energy Based Model)
- イジングモデル(Ising Model)
- イジング模型の目的
エネルギーベースモデル(Energy Based Model)
エネルギーベースモデルとは、エネルギー関数\(E(\mathbf{x} ; \theta)\)と呼ばれる関数を定義し、確率分布を次のように定義するモデルです。
$$P(\mathbf{X} = \mathbf{x} \mid \theta) = \frac{1}{Z(\theta, \beta)}e^{- \beta E(\mathbf{x} ; \theta)}$$
ここで、\(Z(\theta, \beta)\)は規格化定数で次のように定義しました(物理学では規格化定数は分配関数と呼ばれます)
$$Z(\theta, \beta) = \sum_{\mathbf{x}} e^{- \beta E(\mathbf{x} \mid \theta)}$$
\(\sum_{\mathbf{x}} \cdots \)は\(\mathbf{x}\)の取りうる状態全てに関する和を表しています(確率変数が連続値を取る場合は積分となります)
また、\(\beta\)は一般に正の値を取り、逆温度パラメータと呼ばれています。
統計力学の文脈ではエネルギーベースモデルという呼び方は稀ですが、機械学習の文脈では、一般にエネルギーベースモデル[1]と呼ばれます。
逆温度パラメータと呼んでいるのは、統計力学では、\(\beta \equiv 1/k_{B}T\)で定義される量であることが理由です。
『統計力学をしっかり学んでみたい!』という方は、統計力学のおすすめ参考書10選を参考に自分に合った参考書を選んでください。
イジング模型(Ising Model)
エネルギーベースモデルの中でも、確率変数が離散値\(x_{i} \in \{-1, 1\}\)の値を取るモデルは『イジング模型』と呼ばれます。
さらに今回考える例では、確率変数が格子状に定義される模型を考えます。
$$E(\mathbf{x} ; \mathbf{J}) = ~- J \sum_{\langle i, j \rangle} x_{i} x_{j} ~- h \sum_{i} x_{i}$$
各\(i\)は格子点を整数でラベルしたものを表し、各格子点上に確率変数\(x_{i}\)を定義します。
また、\(\langle i, j \rangle\)は隣接\(i, j\)の組みを表し、総和は隣接する変数同士の和を取ることを意味します。
確率分布だけ見ると極めて簡単なモデルに見えますが、格子の形状、パラメータ\(J\), \(h\)に依存して、特徴的なふるまいを見せます。
イジング模型の目的
イジング模型は、簡潔にいうと磁石の性質を明らかにするモデルとして導入されました。
磁石は、とても小さな磁石(スピン)の集合体でモデル化することができ、先ほどの定式化だと各格子点に定義された確率変数\(x_{i}\)が小さな磁石の役割を担い、\(\pm 1\)がそれぞれ磁石のN極とS極に対応します。
もう一度エネルギー関数を眺めてみましょう。
$$E(\mathbf{x} ; \mathbf{J}) = ~- J \sum_{\langle i, j \rangle} x_{i} x_{j} ~- h \sum_{i} x_{i}$$
パラメータ\(J\)が正の場合、隣の小さな磁石は同じ方向を向いた方がエネルギーを小さくすることができます。また、パラメータ\(h\)が正の場合は、小さな磁石はそれぞれ\(+1\)を向いた方がエネルギーを小さくすることができます。
そして、全体として磁石の性質を持つためには、小さな磁石が上または下を向いている割合が0でないことが重要となります。しかし、常にそのような状態が実現するかは自明ではなく、例えば\(\beta \to 0\)極限では、小さな磁石は完全にランダムにふるまい全体として上または下を向いている割合は0となります。
それでは、どのタイミングで全体として上下を向く状態が実現するのでしょうか?そのタイミングを見るのが今回のシミュレーションの目的の一つです。
二次元イジングモデルのシミュレーション
本記事で実験するモデルは正方格子上(2次元)のイジングモデルです。
また、今回は詳細つりあい条件を満たすマルコフ連鎖モンテカルロ法である『メトロポリス法』と『ギブスサンプリング』を使用します。
「マルコフ連鎖モンテカルロ法を使わなくても全体として上下の割合を向く状態が実現するかしないかは分布の平均を評価すれば確かめられる??」という疑問があると思います。
実は、格子が少し大きくなっただけで、規格化定数\(Z(\beta)\)の計算が大変になります(試しに計算してみるのが一番早いです)
そのため、イジング模型はマルコフ連鎖モンテカルロ法を用いてシミュレーションするのが一般的です。
しかし、1次元、2次元、無限次元のイジング模型に関しては、厳密に規格化定数を評価することができます(3次元は現段階で不可能)
今回は、厳密な結果とシミュレーションの結果を比較することができるため二次元格子上のイジング模型を選びました。
マルコフ連鎖モンテカルロ法、メトロポリス法、ギブスサンプリングを理解していない方は、下記の記事を読み終えてから戻ってきてください。

二次元正方格子の2次元イジングモデル
二次元格子点上に確率変数を定義するため格子点を\((i, j)\)と表し、格子点上に定義される確率変数を\(x_{ij}\)とあらわあすことにします。
\(N \times N\)の格子点なら\(i, j\)はそれぞれ\(i=j=1, \ldots, N\)の整数値となります。
そのため、二次元正方格子イジングモデルは、次のエネルギー関数で定義されるエネルギーベースモデルです。
具体的な確率分布はエネルギー関数を代入して以下のように表せます。
$$P(\mathbf{x} \mid \beta, J) = \frac{1}{Z(\beta, J)} \exp \left(\beta J \sum_{ij} x_{i,j} (x_{i+1,j} + x_{i,j+1}) \right)$$
また、分配関数は、以下のように表せます。
$$Z(\beta, J) = \sum_{\mathbf{x}} \exp \left(\beta J \sum_{ij} x_{i,j} (x_{i+1,j} + x_{i,j+1}) \right) $$
メトロポリス法
まずは、メトロポリス法について説明します。
メトロポリス法の受理確率は、エネルギーベースモデルの場合以下のように計算できます。
\begin{align}A(\mathbf{x}, \mathbf{x}^{\prime}) &= \min\left(1, \frac{C(\mathbf{x}|\mathbf{x}^{\prime})}{C(\mathbf{x}|\mathbf{x}^{\prime})} \frac{P(\mathbf{x}^{\prime})}{P(\mathbf{x})}\right) \\ &= \min \left(1, \frac{C(\mathbf{x}|\mathbf{x}^{\prime})}{C(\mathbf{x}|\mathbf{x}^{\prime})} \frac{\exp \left(- \beta E(\mathbf{x}^{\prime};J) \right)}{\exp \left(- \beta E(\mathbf{x};J) \right)} \right)\\&= \min \left(1, \frac{C(\mathbf{x}|\mathbf{x}^{\prime})}{C(\mathbf{x}|\mathbf{x}^{\prime})} \exp \left(-\beta (E(\mathbf{x}^{\prime};J) – E(\mathbf{x};J)) \right) \right) \end{align}
ここで、\(C(\mathbf{x}|\mathbf{x}^{\prime})\)は提案確率を表します。メトロポリス法の提案確率には任意性があります。ランダムに格子点\((i,j)\)の確率変数\(x_{i,j}^{\prime}\)を選び、\(- x_{ij}\)にフリップするような局所的な提案確率を採用すると、受理確率はシンプルに次のように表せます。
$$A(\mathbf{x}, \mathbf{x}^{\prime}) = \min \left(1, \exp \left(-\beta (E(\mathbf{x}^{\prime};J) – E(\mathbf{x};J)) \right) \right)$$
(実際は、ランダムではなくあらかじめ決まった順番を取るように提案しても良いことが示せます。そのため、実装ではこの方法を使用します)
この受理確率からもわかるように、マルコフ連鎖を構成する際に計算が困難であった分配関数\(Z(\beta, J)\)の計算は不要です!!
特に二次元正方格子イジング模型の受理確率は次のように計算できます。
$$A(\mathbf{x}, \mathbf{x}^{\prime}) = \min \left(1, \exp\left(-2J\beta x_{i,j}(x_{i+1,j}+x_{i,j+1}+x_{i-1, j} + x_{i, j-1}) \right) \right)$$
これで、遷移確率を求めることができたのであとはマルコフ連鎖を実際に構成するだけです。
具体的には、以下のようにアルゴリズムを構成します。
メトロポリス法
Input : 任意の初期状態\(\mathbf{x}^{0}\)を設定
- ランダムに\((i, j)\)を選び、\(x_{ij} \to ~-x_{ij}\)のようにフリップする
- 受理確率\(A(\mathbf{x}, \mathbf{x}^{\prime})\)を計算する
- \(0 \le r <1\)の一様乱数\(r\)を発生し、\(r < A(\mathbf{x}, \mathbf{x}^{\prime})\)なら\(x_{i}^{\prime}\)を受理し、そうでなければ棄却する(受理確率で受理する操作)
- ①〜③を繰り返す
ギブスサンプリング
正方格子二次元イジングの場合は、各確率変数\(x_{i}\)の条件付き確率は次の計算することができるので、ギブスサンプリングも利用することができます。
$$P(x_{ij} \mid \mathbf{x} \backslash{x_{ij}}) = \frac{\exp\left(J\beta x_{i,j}(x_{i+1,j}+x_{i,j+1})\right)}{2 \cosh \left(J\beta (x_{i+1,j}+x_{i,j+1}+x_{i-1, j} + x_{i, j-1}) \right)}$$
一応、条件付き分布の途中計算を共有します。
まず、条件付き分布は、\(P(x_{ij} \mid \mathbf{x} \backslash{x_{ij}}) = P(\mathbf{x})/P(\mathbf{x} \backslash{x_{ij}})\)と計算できます。
このとき、\(P(\mathbf{x} \backslash{x_{ij}}) = \sum_{x_{ij}} P(\mathbf{x})\)となり、次のように計算できます。
\begin{align} \sum_{x_{ij}} p(\mathbf{x}) &= \frac{1}{Z} \sum_{x_{ij}} e^{J\beta x_{ij} (x_{i+1, j} + x_{i, j+1}+x_{i-1, j} + x_{i, j-1}) + x_{ij}\text{以外の項}} \\ &= \frac{1}{Z} 2 \cosh(\beta J (x_{i+1, j} + x_{i, j+1}+x_{i-1, j} + x_{i, j-1})) e^{x_{ij}\text{以外の項}} \end{align}
ここで、最後の式変形で\(e^{-ax} + e^{ax} = 2\cosh a\)を用いました。
この結果を\(P(x_{ij} \mid \mathbf{x} \backslash{x_{ij}}) = P(\mathbf{x})/P(\mathbf{x} \backslash{x_{ij}})\)に代入すると
\begin{align} P(x_{ij} \mid \mathbf{x} \backslash{x_{ij}}) &= \frac{e^{\beta J x_{ij} ((x_{i+1, j} + x_{i, j+1}+x_{i-1, j} + x_{i, j-1})}e^{x_{ij}\text{以外の項}}/Z}{2 \cosh(\beta J (x_{i+1, j} + x_{i, j+1}+x_{i-1, j} + x_{i, j-1})) e^{x_{ij}\text{以外の項}}/Z} \\ &= \frac{\exp\left(J\beta x_{i,j}(x_{i+1,j}+x_{i,j+1}+x_{i-1, j} + x_{i, j-1})\right)}{2 \cosh \left(J\beta (x_{i+1,j}+x_{i,j+1}+x_{i-1, j} + x_{i, j-1}) \right)} \end{align}
あとは、この条件付き確率を利用して次のようにマルコフ連鎖を構築するだけです。
ギブスサンプリング
- ランダムに\(i\)を選ぶ
- \(P(x_{ij}=1 \mid \mathbf{x} \backslash{x_{ij}})\)を計算する
- \(0 \le r <1\)の一様乱数\(r\)を発生し、\(r < P(x_{ij}=1 \mid \mathbf{x} \backslash{x_{ij}})\)ならば\(x_{ij} \leftarrow 1\)とし、そうでなければ\(x_{ij} \leftarrow -1\)とする
- ①〜③を繰り返す
二次元イジングモデルで評価する統計量
全体として上または下を向いているかを確かめるためには、全体の小さなスピンの平均値である次の量を評価するのが一つの候補です。
$$m = \frac{1}{N^{2}} \sum_{i, j} x_{ij}$$
これは、統計力学では磁化と呼ばれている量です。この量がある逆温度の値で0から有限値なれば全体として磁石としての役割を担っているかを確かめることができます。
また、やや天下り的ですが、磁化が0から有限値になる際に次で定義される比熱と呼ばれる量が\(N \to \infty\)の極限で発散することが知られています。
$$C = \beta^{2}(\langle E^{2} \rangle – \langle E \rangle^{2})$$
比熱の発散は\(N \to \infty\)でのみ生じますが、有限の\(N\)でもその片鱗を見ることができます。そのため、今回は比熱もチェックしていきましょう。
二次元イジングモデルの実装(Python)

ここからは、二次元イジングモデルの実装方法を紹介します。
具体的には、以下の手順で実装を行います。
- 必要なパッケージをインポート
- イジング模型のクラスを作成
- マルコフ連鎖モンテカルロ法のクラスを作成
- 各逆温度ごとにマルコフ連鎖モンテカルロ法を実装
今回は\(x\)方向の格子の数を\(N_{x}\)、\(y\)方向の格子の数を\(N_{y}\)としました。
必要なパッケージをインポート
まずは、必要なパッケージをインポートしましょう。
import numpy as np
import random
import scipy as sp
from tqdm import tqdm
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML
scipy は2次元イジング模型の厳密解を計算する際に使用します。また、後半のIPython.display等はアニメーションを作成するために使用します。
イジング模型のクラスを作成
コードは少し煩雑になりますが、皆さんが色々遊べるように格子間の相互作用も自由に代入できるよう実装していきます。
そのため、横方向の相互作用\(J_{x}\)と縦方向の相互作用\(J_{y}\)を次のように準備します。
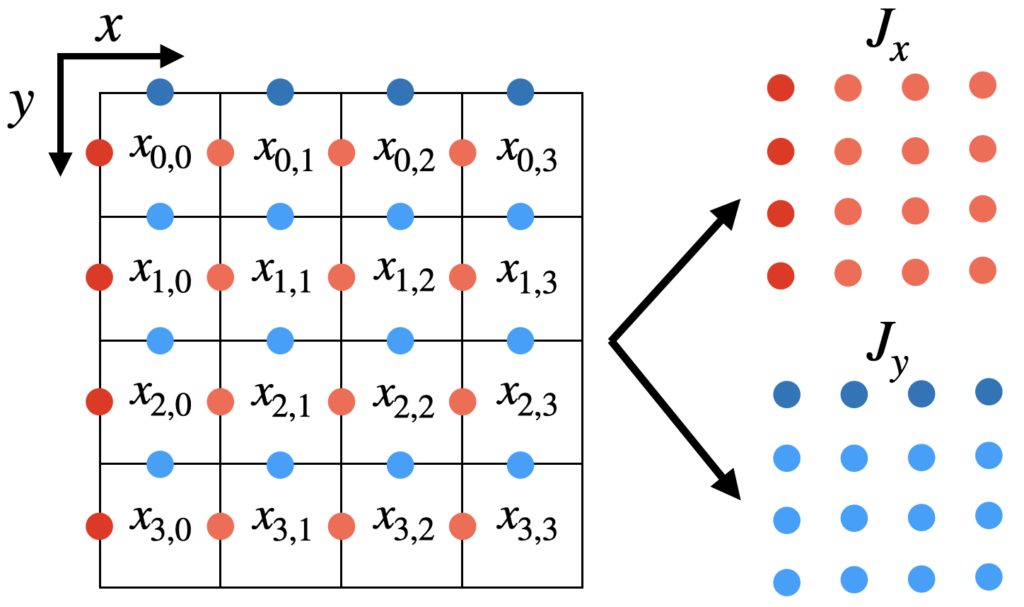
そして、格子のサイズ\(N\)、相互作用配列\(J_{x}, J_{y}\)、磁場\(h\)を属性として持つインスタンスを次のように実装します。
また、周期境界条件を利用します。
class SquareLatticeIsing():
def __init__(self, N, Jx, Jy, h):
"""
Attributes:
N: 格子サイズ
Jx (ndarray (N, N)): x方向の相互作用
Jy (ndarray (N, N)): y方向の相互作用
h: 磁場
"""
self.N=N
self.Jx=Jx
self.Jy=Jy
self.h=h
def neighor_spin_sum(self, state, x, y):
center_spin = state[y, x]
right, left, up, down=x+1, x-1, y-1, y+1
if right>=self.N:
right_spin=state[y, 0]
right_J=self.Jx[y, 0]
else:
right_spin=state[y, right]
right_J=self.Jx[y, right]
if left<0:
left=self.N-1
left_spin=state[y, left]
left_J=self.Jx[y, 0]
else:
left_spin=state[y, left]
left_J=self.Jx[y, left+1]
if up<0:
up=self.N-1
up_spin=state[up, x]
up_J=self.Jy[0, x]
else:
up_spin=state[up, x]
up_J=self.Jy[up+1, x]
if down>=self.N:
down_spin=state[0, x]
down_J=self.Jy[0, x]
else:
down_spin=state[down, x]
down_J=self.Jy[down, x]
neighor_spin_sum=center_spin*(right_J*right_spin+left_J*left_spin+up_J*up_spin+down_J*down_spin)
return neighor_spin_sum
def energy(self, state):
energy=0
for x in range(self.N):
for y in range(self.N):
energy -= self.neighor_spin_sum(state, x, y)/2
energy -= self.h*np.sum(state)
return energy
def magnetization(self, state):
return np.mean(state)
磁化とエネルギーを計算するメソッドを定義しました。
エネルギーでは、二重にカウントすることを考慮して2で割っている点は注意してください。
周期境界条件のコードが複雑だと思う方は、下記を実行して本当に最近接の相互作用とスピンが選ばれることを以下のコードで試してみてください。
# example
Nx, Ny = 4, 4
Jy = np.random.normal(loc= 0, scale=1, size=(4, 4))
Jx = np.random.normal(loc= 0, scale=1, size=(4, 4))
state = np.random.choice([-1, 1], size=(Nx, Ny))
print("spins\n", state)
print("Jx\n", Jx)
print("Jy\n", Jy)
# 中心のスピン
x, y = 0, 0
print(f"center: {(x, y)}", "spin value", state[y, x])
right, left, up, down=x+1, x-1, y-1, y+1
print(f"(right, left, up, down): {(right, left, up, down)}")
if right>=Nx:
right=0
right_spin=state[y, right]
right_J=Jx[y, right]
print("right_spin", right_spin, "right_J", right_J)
else:
right_spin=state[y, right]
right_J=Jx[y, right]
print("right_spin", right_spin, "right_J", right_J)
if left<0:
left=Nx-1
left_spin=state[y, left]
left_J=Jx[y, 0]
print("left_spin", left_spin, "left_J", left_J)
else:
left_spin=state[y, left]
left_J=Jx[y, left+1]
print("left_spin", left_spin, "left_J", left_J)
if up<0:
up=Ny-1
up_spin=state[up, x]
up_J=Jy[0, x]
print("up_spin", up_spin, "up_J", up_J)
else:
up_spin=state[up, x]
up_J=Jy[up+1, x]
print("up_spin", up_spin, "up_J", up_J)
if down>=Ny:
down=0
down_spin=state[down, x]
down_J=Jy[down, x]
print("down_spin", down_spin, "down_J", down_J)
else:
down_spin=state[down, x]
down_J=Jy[down, x]
print("down_spin", down_spin, "down_J", down_J)
マルコフ連鎖モンテカルロ法を実装
次にマルコフ連鎖モンテカルロ法を実装していきます。
class IsingMC():
def __init__(self, method):
self.method=method
def run_mcmc(self, dist, init_state, n_step=1000, beta=1.0):
state=init_state
state_dynamics=np.zeros((n_step+1, dist.N, dist.N))
state_dynamics[0]=state
AR_dynamics=[]
for step in tqdm(range(n_step)):
if self.method=="gibbs":
state, AR = self.step_Gibbs(dist, state, beta=beta)
else:
state, AR = self.step_MH(dist, state, beta=beta)
AR_dynamics.append(AR)
state_dynamics[step+1] = state
print(f'ACCEPTANCE RATE : {np.mean(AR_dynamics):.3f}')
return state_dynamics, AR_dynamics
def step_MH(self, dist, state, beta=1.0):
# select rule
flip_order_x = list(range(dist.N))
flip_order_y = list(range(dist.N))
random.shuffle(flip_order_x)
random.shuffle(flip_order_y)
n_flg = 0
for x in flip_order_x:
for y in flip_order_y:
delta_energy = 2*(dist.neighor_spin_sum(state, x, y)+dist.h*state[y, x])
trans_prob = np.exp(-beta*delta_energy)
if np.random.random()<=trans_prob:
state[y, x] *= -1
n_flg += 1
return state, n_flg/(dist.N*dist.N)
def step_Gibbs(self, dist, state, beta=1.0):
# select rule
flip_order_x = list(range(dist.N))
flip_order_y = list(range(dist.N))
random.shuffle(flip_order_x)
random.shuffle(flip_order_y)
for x in flip_order_x:
for y in flip_order_y:
neighors = (dist.neighor_spin_sum(state, x, y)+dist.h*state[y, x])/state[y, x]
trans_prob = np.exp(beta*neighors)/(np.exp(beta*neighors)+np.exp(-beta*neighors))
if np.random.random()<=trans_prob:
state[y, x] *=1
else:
state[y, x] *=-1
return state, 1.0
『method』の引数を変えることでメトロポリス法, ギブスサンプリングどちらを利用するかを選択できるようにしました。
動作を簡単に確かめるために\(32\times 32\)のイジング模型を作り、\(\beta=0.5\)の場合で、メトロポリス法を走らせてみましょう。
# Ising Instance
N, h=32, 0.0
Jx=np.ones((N, N))
Jy=np.ones((N, N))
dist=SquareLatticeIsing(N, Jx, Jy, h)
# MCMC Instance
n_step=1500
init_state = np.random.choice([-1,1], size=(dist.N,dist.N))
sampler=IsingMC(method="metropolis")
state_dynamics, AR_dynamics = sampler.run_mcmc(dist, init_state, beta=0.5, n_step=n_step)
それでは、磁化とエネルギーの値をプロットしてみます。
m_dynamics = np.array([dist.magnetization(state) for state in state_dynamics])
energy_dynamics = np.array([dist.energy(state)/(dist.N*dist.N) for state in state_dynamics])
fig, axes=plt.subplots(1, 2, figsize=(8, 3), constrained_layout=True, dpi=200)
axes[0].plot(m_dynamics)
axes[0].set_xlabel(r"$t$", fontsize=16)
axes[0].set_ylabel(r"$m$", fontsize=16)
axes[0].grid()
axes[1].plot(energy_dynamics)
axes[1].set_ylabel(r"$E/N^2$", fontsize=16)
axes[1].set_xlabel(r"$t$", fontsize=16)
axes[1].grid()
plt.show()<output>
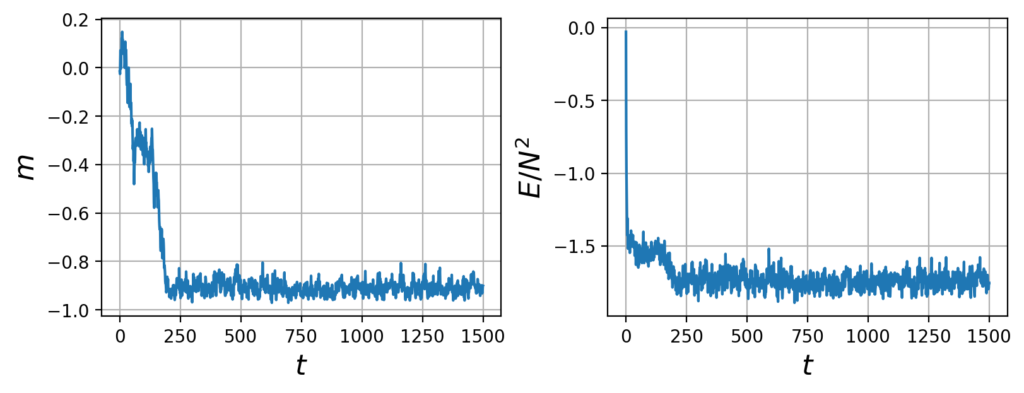
それでは、少し大きめのサイズのMCMCのアニメーションを作ってみます。下記のコードでアニメーションをみることができるので逆温度の値を変えて遊んでみてください。
# Ising Instance
N, h=256, 0.0
Jx=np.ones((N, N))
Jy=np.ones((N, N))
dist=SquareLatticeIsing(N, Jx, Jy, h)
n_step=100
# MCMC Instance
init_state = np.random.choice([-1,1], size=(dist.N,dist.N))
sampler=IsingMC(method="metropolis")
state_dynamics, AR_dynamics = sampler.run_mcmc(dist, init_state, beta=0.44, n_step=n_step)
fig, ax = plt.subplots()
ims = []
ani_step=100
for step in range(ani_step):
ax.axis("off")
im = ax.imshow(state_dynamics[step], animated=True, cmap="gray")
ims.append([im])
anim = animation.ArtistAnimation(fig, ims)
rc('animation', html='jshtml')
plt.close()
anim

matplotlibでアニメーションを作成する方法をある程度体系的に学びたいという方は下記を参考にしてみてください。
各逆温度ごとにマルコフ連鎖モンテカルロ法を実行
最後に各逆温度ごとにマルコフ連鎖モンテカルロ法を実行するコードを紹介します。
今回は、時間の都合から\(64 \times 64\)の格子に対して実行していきます(短時間で終わらせたい方は、\(N=32\)にするか逆温度間隔betasを調節してください )
# Ising Instance
N, h=64, 0.0
Jx=np.ones((N, N))
Jy=np.ones((N, N))
dist=SquareLatticeIsing(N, Jx, Jy, h)
# MCMC Instance
betas=np.linspace(0.05, 0.8, 35)
n_step, burn_in, interval=2500, 100, 10
init_state=np.random.choice([-1,1], size=(dist.N,dist.N))
sampler=IsingMC(method="metropolis")
betas_m, betas_m_err=[], []
betas_per_energy, betas_per_energy_err=[], []
betas_per_capacity=[]
for beta in betas:
print(f"【beta】: {beta:.3f}")
state_dynamics, AR_dynamics = sampler.run_mcmc(dist, init_state, beta=beta, n_step=n_step)
# burn in and interval
state_dynamics=state_dynamics[burn_in::interval]
# magnetization
beta_m_samples=np.array([dist.magnetization(state) for state in state_dynamics])
beta_m=np.mean(beta_m_samples)
beta_m_err=np.std(beta_m_samples)/(np.sqrt(len(beta_m_samples)))
# energy density
beta_per_energy_samples=np.array([dist.energy(state)/(dist.N*dist.N) for state in state_dynamics])
beta_per_energy=np.mean(beta_per_energy_samples)
beta_per_energy_err=np.std(beta_per_energy_samples)/(np.sqrt(len(beta_per_energy_samples)))
# capacity density
beta_energy_samples=np.array([dist.energy(state) for state in state_dynamics])
beta_square_energy_samples=np.array([(dist.energy(state))**2 for state in state_dynamics])
beta_energy=np.mean(beta_energy_samples)
beta_squre_energy=np.mean(beta_square_energy_samples)
beta_per_capacity=((beta**2)*(beta_squre_energy-(beta_energy**2)))/((dist.N*dist.N))
betas_m.append(beta_m)
betas_m_err.append(beta_m_err)
betas_per_energy.append(beta_per_energy)
betas_per_energy_err.append(beta_per_energy_err)
betas_per_capacity.append(beta_per_capacity)
実は、二次元イジング模型は、高度な理論解析により厳密解を得ることができます。
その結果、転移点は次のように表せます。
$$\beta_{c}=\frac{\log (1+\sqrt{2})}{2 J} \approx 0.441$$
また、磁化、エネルギー密度、比熱密度は次のように計算することができます。
\begin{align} &|m| = \begin{cases} 0 & \beta < \beta_{c} \\ \left(1- \frac{1}{\sinh^{4}(2 \beta)} \right)^{1/8} & \beta>\beta_{c} \end{cases} \\ &E/N^{2} = – J \coth (2\beta) \left(1 + \frac{2}{\pi} \zeta^{\prime} K(\zeta) \right) \\ &C/N^{2} = \frac{4(\beta \coth 2 \beta)^{2}}{\pi} \left(K(\zeta)-E(\zeta) – \frac{(1-\zeta^{\prime})}{2} \left(\frac{\pi}{2} + \zeta^{\prime} K(\zeta) \right) \right) \end{align}
それぞれ、次のように定義しました。
\begin{align} &\zeta=2 \tanh(2\beta)/\cosh(2\beta) \\ &\zeta^{\prime}=2 \tanh^{2}(2\beta)-1 \\ &K(x) = \int_{0}^{\pi/2} \frac{1}{\sqrt{1-x^{2} \sin^{2} t}} dt \\ &E(x) = \int_{0}^{\pi/2} \sqrt{1-x^{2} \sin^{2} t} dt \end{align}
\(K(x)\)、\(E(x)\)は、それぞれ第一種および第二種完全楕円積分と呼ばれ、scipyのscipy.special.ellipk(x), scipy.special.ellipe(x)により簡単に計算することができます(詳細は公式ドキュメントへ: scipy.special.ellipk, scipy.special.ellipe)
それぞれを計算するコードを共有します。
def exact_m_abs(beta):
exact_m=(1-(1/(np.sinh(2*beta)**4)))**(1/8)
exact_m[beta < np.log(1+np.sqrt(2))/2]=0
return exact_m
def exact_per_energy(beta):
zeta=2*(np.tanh(2*beta)/np.cosh(2*beta))
diff_zeta=2*(np.tanh(2*beta)**2)-1
K = sp.special.ellipk(zeta**2)
exact_per_energy = - (1/np.tanh(2*beta))*(1+ (2*diff_zeta*K)/(np.pi))
return exact_per_energy
def exact_per_capacity(beta):
zeta=2*(np.tanh(2*beta)/np.cosh(2*beta))
diff_zeta=2*(np.tanh(2*beta)**2)-1
K=sp.special.ellipk(zeta**2)
E=sp.special.ellipe(zeta**2)
coff=(2/np.pi)*((beta/np.tanh(2*beta))**2)
exact_per_capacity=coff*(-(1-diff_zeta)*((np.pi/2)+diff_zeta*K)-2*E+2*K)
return exact_per_capacity
これで準備ができたのいよいよ厳密解とシミュレーションの結果を図示します。
# 厳密解
betas_exact = np.linspace(0.05, 0.8, 1000)
betas_exact_m = exact_m_abs(betas_exact)
betas_exact_per_energy = exact_per_energy(betas_exact)
betas_exact_per_capacity = exact_per_capacity(betas_exact)
fig, axes = plt.subplots(3, 1, figsize=(5, 8), constrained_layout=True, dpi=200)
axes[0].plot(betas, np.abs(betas_m), c="k", marker='o', mfc="None", label=r"$64 \times 64$")
axes[0].plot(betas_exact, betas_exact_m, ls="--", color="r", label=r"$Exact$")
axes[0].set_xlabel(r"$\beta$", fontsize=16)
axes[0].set_ylabel(r"$|m|$", fontsize=16)
axes[0].legend(fontsize=12)
axes[0].grid()
axes[1].plot(betas, betas_per_energy, c="k", marker='o', mfc="None", label=r"$64 \times 64$")
axes[1].plot(betas_exact, betas_exact_per_energy, ls="--", color="r", label=r"$Exact$")
axes[1].set_xlabel(r"$\beta$", fontsize=16)
axes[1].set_ylabel(r"$E/N^{2}$", fontsize=16)
axes[1].legend(fontsize=12)
axes[1].grid()
axes[2].plot(betas, betas_per_capacity, color="k", marker='o', mfc="None", label=r"$64 \times 64$")
axes[2].plot(betas_exact, betas_exact_per_capacity, ls="--", color="r", label=r"$Exact$")
axes[2].set_xlabel(r"$\beta$", fontsize=16)
axes[2].set_ylabel(r"$C/N^{2}$", fontsize=16)
axes[2].legend(fontsize=12)
axes[2].grid()
plt.show()<output>
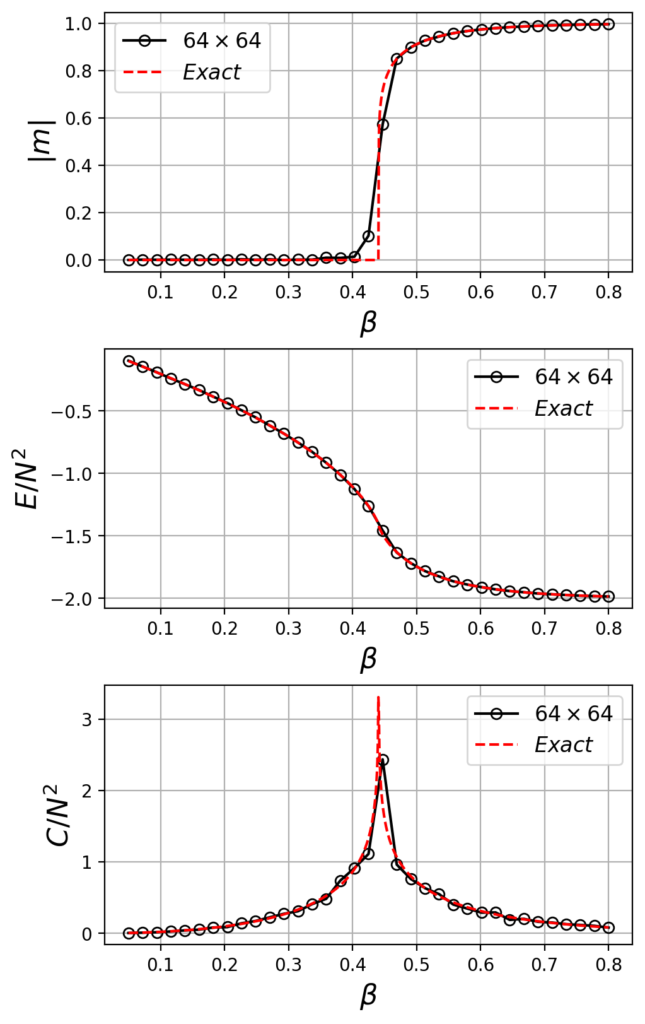
\(64 \times 64\)のシミュレーションの結果でも厳密解とある程度一致し、転移点\(\beta_{c}\)近傍で磁化の値が非ゼロとなり、比熱発散の片鱗のようなものを見ることができました!
参考資料
本記事を作成するために使用した資料を紹介していきます。
参考文献
[1] : LeCun, Yann, et al. “A tutorial on energy-based learning.” Predicting structured data 1.0 (2006).
参考書籍
まずは、参考文献を紹介します。
統計科学のフロンティア 12 計算統計II マルコフ連鎖モンテカルロ法とその周辺 (岩波オンデマンドブックス)
モンテカルロ法を学ぶのに最適な一冊です。
二次元イジングモデル以外にも詳しい説明が載っています。
ゼロからできるMCMC マルコフ連鎖モンテカルロ法の実践的入門 (KS理工学専門書)
モンテカルロの理論だけでなく、実装も載っています。
相転移・臨界現象とくりこみ群
二次元イジングというよりも相転移の体系的な知識を習得することができます。
これならわかる機械学習入門 (KS物理専門書)
本記事で扱った二次元イジングモデルの実装も載っています。
さらに、最後の章には、イジングモデル&機械学習の論文を再現するという章がありとても面白いです。
参考URL
参考にしたWeb上の情報を共有します。
- Ising Model : より詳しい内容が載っています(ドメイン成長過程についても扱っています)
- Monte Carlo method applied on a 2D binary alloy using an Ising Model on Python
まとめ
今回は、イジングモデルと呼ばれる確率モデルに対してマルコフ連鎖モンテカルロ法を適用した例を紹介しました。
モンテカルロ法の基本的な理論は下記を参考にしてください。


Pythonを学習するのに効率的なサービスを紹介していきます。
まず最初におすすめするのは、Udemyです。
Udemyは、Pythonに特化した授業がたくさんあり、どの授業も良質です。
また、セール中は1500円定義で利用することができ、コスパも最強です。
下記の記事では、実際に私が15個以上の講義を受講して特におすすめだった講義を紹介しています。

他のPythonに特化したオンライン・オフラインスクールも下記の記事でまとめています。

自分の学習スタイルに合わせて最適なものを選びましょう。
また、私がPythonを学ぶ際に使用した本を全て暴露しているので参考にしてください。