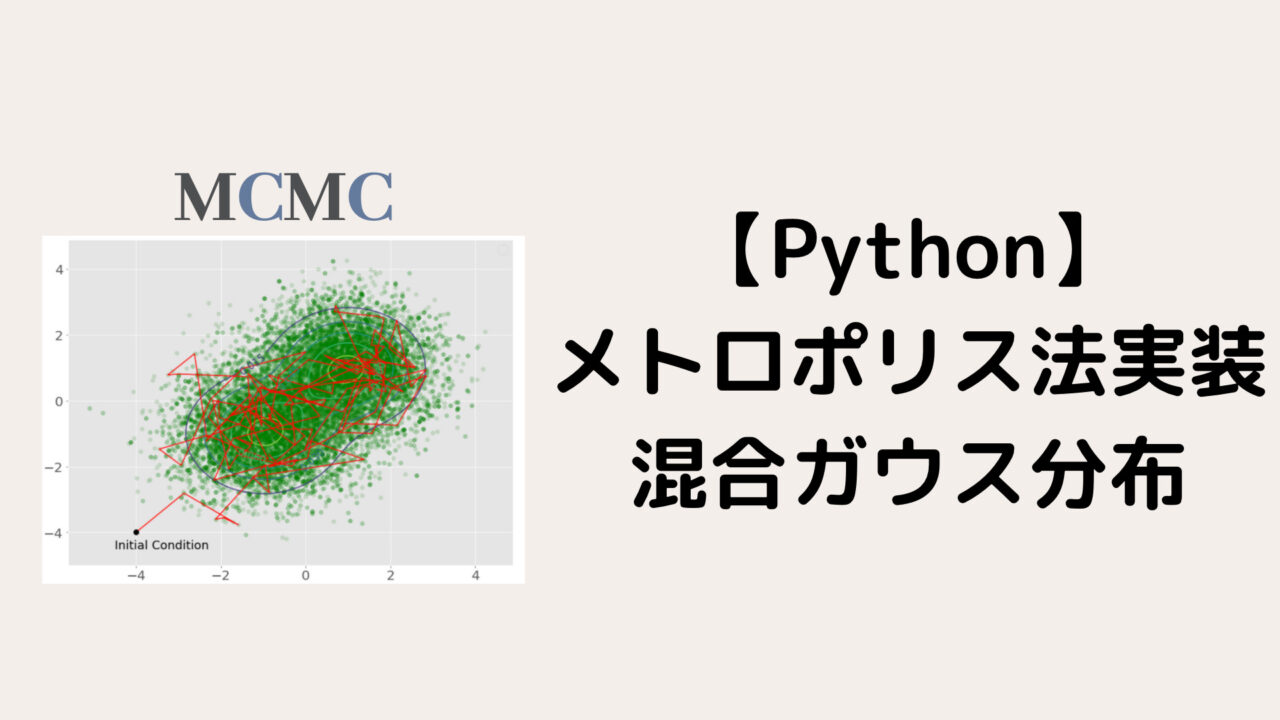
【Python】メトロポリス・ヘイスティング法の応用(多変量混合ガウス分布)
本記事では、マルコフ連鎖モンテカルロ法の一つであるメトロポリス・ヘイスティング法(Metropolis Hastings Method)を多変量ガウス分布に適用した例を紹介します。
前半部分ではメトロポリス・ヘイスティング法と多変量ガウス(特に二変量ガウス分布)について説明し、後半ではPythonによる実装を行います。
マルコフ連鎖モンテカルロ法を聞いたことがない方は下記を一読してから本記事を読んでください。

メトロポリス・ヘイスティング法について

メトロポリス・ヘイスティング法の目的は、規格化定数(正規化定数)がわからない確率分布\(p(\mathbf{x})\)からサンプリングを行うことです。
そして、メトロポリス・ヘイスティング法では遷移確率\(W(\mathbf{x} \to \mathbf{x}^{\prime}\)を以下のように分解したマルコフ連鎖を用いて\(p(\mathbf{x})\)からサンプリングを行います。
メトロポリス・ヘイスティング法の遷移確率
$$W(\mathbf{x} \to \mathbf{x}^{\prime}) = C(\mathbf{x}^{\prime} \mid \mathbf{x}) A(\mathbf{x}, \mathbf{x}^{\prime})$$
- \(C(\mathbf{x}^{\prime} \mid \mathbf{x}) : 提案確率(次の遷移の候補を選択する確率)
- \(A(\mathbf{x}, \mathbf{x}^{\prime})\) : 受理確率(候補を受理する確率)で以下で定義される。
$$A(\mathbf{x}, \mathbf{x}^{\prime}) = \min \left(1, \frac{P(\mathbf{x}^{\prime}) C(\mathbf{x} \mid \mathbf{x}^{\prime})}{P(\mathbf{x}) C(\mathbf{x}^{\prime} \mid \mathbf{x})} \right)$$
この遷移確率を用いることで、目的の確率分布\(P(\mathbf{x})\)を定常分布として持つマルコフ連鎖を構築することができます。
『マルコフ連鎖??』という方や詳しい証明に興味がある方は下記を参考にして下さい。

混合ガウス分布の基本知識

ここでは、今回サンプリングを行う混合ガウス分布の基本知識を整理します。
混合ガウス分布の定義
混合ガウス分布は、まさにガウス分布を混ぜたような分布で以下のように定義されます。
定義 : 混合ガウス分布
混合ガウス分布とは以下で定義された確率密度関数である。
\begin{align}&P(\mathbf{x} ; \{\mu_{k}\}_{k=1}^{K}, \{\Sigma_{k}\}_{k=1}^{K}, \{\pi_{k}\}_{k=1}^{K}) \\ = &\sum_{k=1}^{K} \pi_{k} \mathcal{N}(\mathbf{x} \mid \mu_{k}, \Sigma_{k}) \end{align}
ここで、\(\pi\)は混合の割合を表す係数で、以下の条件を満たす。
$$\sum_{k=1}^{K} \pi_{k} = 1$$
『式を表示されても具体的なイメージがわからない…』という方も多いと思います。
そこで、以下の一次元混合ガウス分布を例に可視化を行います。
$$P(x) = 0.5 \mathcal{N}(0, 1) + 0.25*\mathcal{N}(4, 1) + 0.25 \mathcal{N}(-4, 1)$$
プロットすると以下のように三つのガウス分布を混ぜたような形状をしています。
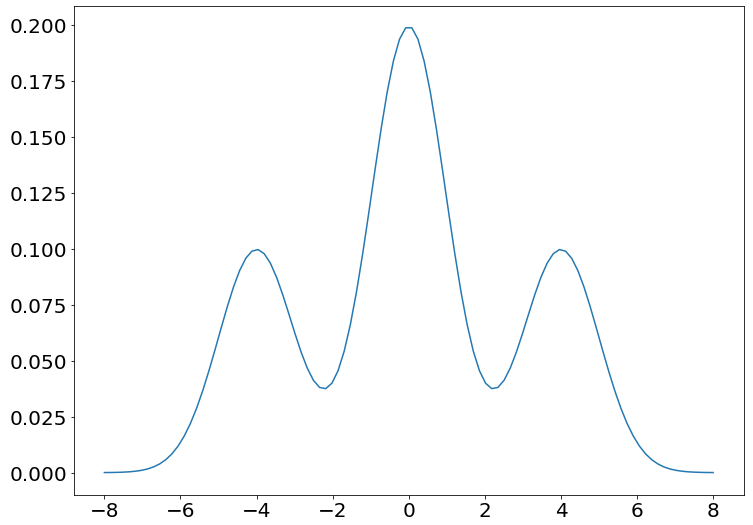 一次元混合ガウス分布の具体例
一次元混合ガウス分布の具体例
今回はもう少し複雑な混合二変量ガウス分布からのサンプリングを行います。
メトロポリス法の適用(二変量ガウス分布)

ここではメトロポリス法の適用方法を紹介します。
メトロポリス法の遷移確率は提案確率\(C(\mathbf{x}^{\prime} \mid \mathbf{x})\)以下のように表せることを思い出しましょう。
\begin{align}W(\mathbf{x} \to \mathbf{x}^{\prime}) &= C(\mathbf{x}^{\prime} \mid \mathbf{x}) A(\mathbf{x}, \mathbf{x}^{\prime}) \\ &= C(\mathbf{x}^{\prime} \mid \mathbf{x}) \min \left(1, \frac{P(\mathbf{x}^{\prime})}{P(\mathbf{x})} \right) \end{align}
二変量ガウス分布の場合、受理確率に現れる確率密度の比は簡単に計算できます。
提案分布に関しては、対称な確率分布ならなんでも良いですが、今回は提案分布として以下のようにガウス分布を選ぶことにします。
\begin{align} x^{\prime} &\sim C(x^{\prime} \mid x) = \mathcal{N}(x, \sigma^{2}) \\ y^{\prime} &\sim C(y^{\prime} \mid y) = \mathcal{N}(y, \sigma^{2}) \end{align}
ここで、\(\sigma^{2}\)はユーザーが決定するパラメータとなります。
直感的に、\(\sigma\)を大きくすることで大きく状態を更新できますが、受理される確率が減ることが予想できます。
この後の実装例で\(\sigma\)を変化させたときに同様な変化が見られるか実際に確認するので楽しみにしてください。
ここまでの話をまとめ以下にメトロポリス法のアルゴリズムをまとめます。
メトロポリス法(二変量ガウス分布)
- 適当に初期状態\(x^{0}\), \(y^{0}\)を設定
- 以下を繰り返す
- \(x^{\prime}\)を\(C(x^{\prime} \mid x)\)で提案
- \(y^{\prime}\)を\(C(y^{\prime} \mid y\)で提案
- 受理確率\(A(\mathbf{x}, \mathbf{x}^{\prime})\)で提案されたサンプル\(\mathbf{x}^{\prime}\)をサンプル列に加える
メトロポリス法の実装(Python)
ここからは、Pythonによるメトロポリス法の実装を紹介します。
まずは、使用するライブラリをインポートしてください。
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(0)
from scipy import stats
# 3次元プロットの準備
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams["axes.facecolor"] = 'white'
# プロットのスタイル
plt.style.use('ggplot')
混合二変量ガウス分布をプロット
まずは、以下のように混合二変量ガウス分布を定義します。
def mgauss(pos, mus, sigmas, pi=0.5):
norm1 = stats.multivariate_normal.pdf(pos, mean=mus[0], cov=sigmas[0])
norm2 = stats.multivariate_normal.pdf(pos, mean=mus[1], cov=sigmas[1])
return pi*norm1 + (1-pi)*norm2
『pos』には二次元配列を代入してください。
今回サンプリングする確率分布は、以下の平均と分散共分散行列を持つ混合ガウス分布とします。
サンプリングを行う混合ガウス分布のパラメータ
- 平均
$$\vec{\mu}_{1} = \left(\begin{array}{c} -1 \\ -1 \end{array} \right),~~\vec{\mu}_{2} = \left(\begin{array}{c} 1 \\ 1 \end{array} \right)$$
- 分散共分散行列
$$\Sigma_{1} = \Sigma_{2} = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1\end{array} \right)$$
- 混合率
$$\pi_{1} = \pi_{2} = \frac{1}{2}$$
このようなパラメータをまとめて以下のように定義しておきます。
mus = np.array([[-1, -1], [1,1]])
sigmas = np.array([[[1.0, 0.0], [0.0, 1.0]],
[[1.0, 0.0], [0.0, 1.0]]])
このパラメータのときの二次元混合ガウス分布の等高線を以下に表示します。
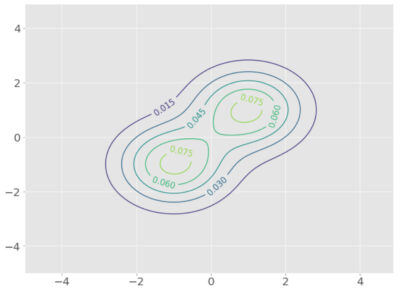
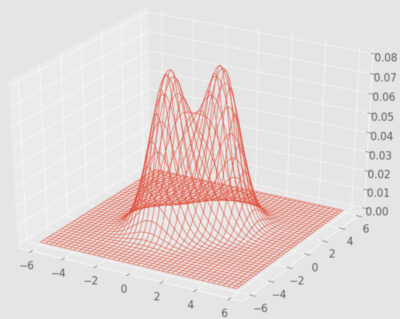
また、3次元プロットを以下に表示します。
メトロポリス法のアルゴリズム
先ほど紹介した二変量混合ガウス分布に関するメトロポリス法を実装していきます。
実装例を以下に示します。
def metropolis_method(x_init=[0, 0], steps=1000, scale=0.1):
samples = [x_init]
x, y = x_init[0], x_init[1]
accepted_num = 0
for i in range(steps):
prop_x, prop_y = np.random.normal(loc=x, scale=scale), np.random.normal(loc=y, scale=scale)
accept_prob = mgauss([prop_x, prop_y], mus, sigmas)/mgauss([x, y], mus, sigmas)
if np.random.rand() <= accept_prob:
x, y = prop_x, prop_y
accepted_num += 1
samples.append([x, y])
print(f'ACCEPTANCE RATE : {(accepted_num/steps):2f}')
return samples, accepted_num
メトロポリス法の実行
初期状態として、(-4, -4)を選びメトロポリス法を実行してみます。
# メトロポリス法実行
x_init = [-4, -4]
samples, acceptance_rate = metropolis_method(x_init=x_init, steps=10000, scale=1)
samples = np.array(samples)
実行結果を先ほどの等高線プロットで表示します。
fig, ax = plt.subplots(figsize=(12, 9))
ax.scatter(samples[:, 0], samples[:, 1], alpha=0.15, c='g')
ax.plot(samples[:200, 0], samples[:200, 1], c='r')
ax.plot(x_init[0], x_init[1], marker='.', ms=15, c='k')
cntr = ax.contour(X, Y, Z)
ax.clabel(cntr, fontsize=15)
ax.annotate('Initial Condition', xy=(x_init[0]-0.5, x_init[1]-0.5), fontsize=18)
plt.legend(fontsize=17)
plt.tick_params(axis='y', labelsize=20)
plt.tick_params(axis='x', labelsize=20)
plt.figure()
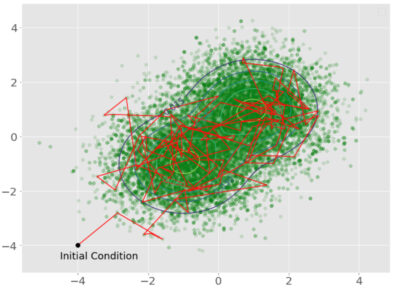 最初の200サンプルを赤線で繋いだ
最初の200サンプルを赤線で繋いだ
実行結果を3次元ヒストグラムに表示します。
x = np.arange(-6.0, 6.0, 0.1)
y = np.arange(-6.0, 6.0, 0.1)
X, Y = np.meshgrid(x, y)
pos = np.dstack((X, Y))
Z = mgauss(pos, mus, sigmas)
hist, x_edges, y_edges = np.histogram2d(samples[:, 0], samples[:, 1], bins=30, density=True)
X_hist, Y_hist = np.meshgrid(x_edges[:-1], y_edges[:-1])
Z_hist = 0
dx = X_hist[0, 1] - X_hist[0, 0]
dy = Y_hist[1, 0] - Y_hist[0, 0]
dz = hist.ravel()
X_hist = X_hist.ravel()
Y_hist = Y_hist.ravel()
fig, ax = plt.subplots(figsize=(12, 9), subplot_kw={'projection' : '3d'})
surface = ax.plot_wireframe(X, Y, Z, linewidth=1.5)
# ax.view_init(elev=40, azim=10)
ax.bar3d(X_hist, Y_hist, Z_hist, dx, dy, dz, alpha=0.1, color='c')
plt.tick_params(axis='y', labelsize=15)
plt.tick_params(axis='x', labelsize=15)
plt.tick_params(axis='z', labelsize=15)
plt.show()
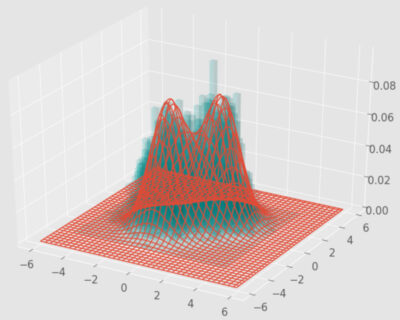
おおよそ混合ガウス分布からのサンプリングに成功していることがわかります。
まとめ
本記事では、混合ガウス分布を用いてメトロポリス法の実装例を紹介しました。
皆さんもパラメータを変えて遊んでみてください。

『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。