本記事では、マルコフ連鎖を利用しない静的なモンテカルロと呼ばれる手法の一つである『重点サンプリング』を簡単に説明して、そのアルゴリズムをPythonで実装します。
重点サンプリング（Importance Sampling)の基本
まずは、重点サンプリング（Importance Sampling）の解説を行います。
サンプリングを用いた期待値評価
まず、対象となる離散確率分布を次のように定義します。
$$p(x) = \frac{1}{Z_{p}} \tilde{p}(x)$$
ここで、\(Z_{p}\)は規格化定数で、次の関係を満たします。
$$Z_{p} = \int dx \tilde{p}(x)$$
そして、この確率分布に従う確率変数\(x\)に関する関数\(f(x)\)の期待値を\(\mathbb{E}_{p(x)}[f(x)]\)とおくと、期待値は次のように定義されます。
$$\mathbb{E}_{p(x)}[f(x)] = \int dx p(x) f(x)$$
一般的に、この積分を実行できるケースはごくわずかです（正規分布等の特殊な確率分布の場合は積分が実行できる可能性があります）
また、グリットに分けて数値計算を行う手法も次元が大きくなると現実的な時間で実行不可能となります。仮に\(n\)次元変数に関する積分を10個のグリットに分けて行う場合、\(10^{n}\)の和を計算する必要があります泣
これらの問題を解決するために、モンテカルロ法のアイデアが有効です！
具体的に、モンテカルロ法のアイデアは以下の通りです。
- 確率分布\(P(\mathbf{x})\)に従うサンプル列\(\{\mathbf{x}\}_{t=1}^{T}\)を生成
- そのサンプルに関する平均（標本平均）により、期待値計算を近似的に評価
具体的には以下のように近似を行います。
モンテカルロ法による期待値評価
$$\mathbb{E}[f(\mathbf{x})] \approx \frac{1}{T} \sum_{t=1}^{T} f(\mathbf{x}^{t})$$
確率論の定理（中心極限定理）から、モンテカルロ法の期待値評価は、サンプル数\(T \to \infty\)の極限で真の期待値に収束します。
また、モンテカルロ法の期待値評価による誤差は、変数の次元に依存せずに減少していきます。
期待値の問題を『確率分布からのサンプリング問題』に変換することができました。
具体的な例を通して、サンプリングによる期待値近似を理解したい方は、モンテカルロ法のイメージのサイコロの例を一読してみてください。
＊本記事で『サンプリング』と言った場合は、数式で与えられた確率分布から具体的なサンプル（列）を生成することを意味しています。
重点サンプリングの目的
ここまで、確率分布\(p(x)\)に従う期待値が確率分布\(p(x)\)からのサンプリング問題により近似できることを紹介しました。
しかし、一般的に確率分布\(p(x)\)の規格化定数\(Z_{p}\)が簡単に計算できる場合は稀です。そのため、\(p(x)\)からのサンプリングもそこまで容易ではありません。
重点サンプリングは、規格化定数が未知でサンプリングが困難な\(p(x)\)に従う確率変数\(x\)の期待値やその規格化定数を別のサンプリングが容易な確率分布\(q(x)\)からサンプリングにより解決する手法です。
詳細は、以降説明していきます。その前に簡単にこれまでの流れをまとめておきます。
これまでの流れ
- 確率分布\(p(x)\)に従う確率変数\(x\)の期待値を計算したい計算量的に困難…
- 確率分布\(p(x)\)のサンプリングにより期待値が近似できる！
- ただ、確率分布\(p(x)\)からのサンプリングも一般的には困難…
- 重点サンプリング: サンプリングが容易な確率分布\(q(x)\)を上手く使って上記を解決！
重点サンプリングの仕組み
重点サンプリングでは、まずサンプリングが容易かつ規格化定数が既知の確率分布\(q(x)\)を用意します。
$$q(x) = \frac{1}{Z_{q}} \tilde{q}(x)$$
ここで、\(Z_{q}\)は規格化定数で容易に計算可能であることを仮定します。以降、この分布\(q(x)\)を提案分布と呼ぶことにします。
また、この確率分布\(q(x)\)は以下の条件を満たす必要があります。
\(q(x)\)の条件
\(p(x) \neq 0\)となる任意の\(x\)に対して\(q(x) \neq 0\)となる。
以降の解説では、確率分布\(p(x)\)の期待値を\(\mathbb{E}_{p(x)}[\cdot]\)と表して、確率分布\(q(x)\)の期待値を\(\mathbb{E}_{q(x)}[\cdot]\)と表すことにします。
重点サンプリングは、ある統計量\(A(x)\)の期待値が、以下のような式変形で、サンプリングが容易な確率分布\(q(x)\)の期待値問題になることを利用します。
\begin{align} \mathbb{E}_{p(x)}[A(x)] &= \int A(x) p(x) dx \\ &= \int A(x) \frac{p(x)}{q(x)} q(x) dx \\&= \mathbb{E}_{q(x)} \left[A(x) \frac{p(x)}{q(x)} \right] \end{align}
この単純な式変形により、\(p(x)\)に従う確率変数\(x\)の\(A(x)\)の期待値を計算する問題が、\(q(x)\)に従う確率変数\(x\)の\(A(x) p(x)/q(x)\)の期待値を計算する問題に帰着されます。
さらに式変形を進めると次のように表せます。
\begin{align} \mathbb{E}_{q(x)} \left[A(x) \frac{p(x)}{q(x)} \right] &= \int q(x) A(x) \frac{p(x)}{q(x)} dx \\ &=\frac{Z_{q}}{Z_{p}} \int q(x) A(x) \frac{\tilde{p}(x)}{\tilde{q}(x)} dx \\ &=\frac{Z_{q}}{Z_{p}} \frac{1}{M} \sum_{m=1}^{M} A(x^{(m)})\frac{\tilde{p}(x^{(m)})}{\tilde{q}(x^{(m)})} \\&= \frac{Z_{q}}{Z_{p}} \frac{1}{M} \sum_{m=1}^{M} A(x^{(m)}) w(x^{(m)})\end{align}
ここで、\(w^{(m)}\)は以下のように定義しました。
$$w(x^{(m)}) := \frac{\tilde{p}(x^{(m)})}{\tilde{q}(x^{(m)})}$$
一般的に\(w^{(m)}\)は重要度重み（importance weight）と呼ばれます。
また, \(x^{(m)}\)は、\(p(x)\)ではなく\(q(x)\)からのサンプル点です。
あとは、規格化定数\(Z_{p}\)が計算できれば、\(A(x)\)の期待値が評価できます。
この後すぐに説明しますが、規格化定数\(Z_{p}\)も重要度重みを用いて評価することができます。
\(q(x)\)の『\(p(x) \neq 0\)となる任意の\(x\)に対して\(q(x) \neq 0\)となる』という条件は、重要度重みが適切に定義されるように要請しています。
規格化定数の計算
規格化定数は、重要度重みのサンプル平均により計算することができます。
実際、規格化定数の比は、以下のように変形できます。
\begin{align} \frac{Z_{p}}{Z_{q}} &= \frac{1}{Z_{q}} \int \tilde{p}(x) dx \\ &= \int \frac{\tilde{p}(x)}{\tilde{q}(x)} q(x) dx \\ &\approx \frac{1}{M} \sum_{m=1}^{M} w(x^{(m)}) \end{align}
いま、\(Z_{q}\)は、既知なので規格化は以下のように計算することができます。
$$Z_{p} \approx \frac{Z_{q}}{M} \sum_{m=1}^{M} w(x^{(m)})$$
この結果を統計量\(A(x)\)の期待値評価の式に代入すると、期待値は以下のように評価することができます。
\begin{align} \mathbb{E}_{p(x)}[A(x)] &\approx \frac{Z_{q}}{Z_{p}} \frac{1}{M} \sum_{m=1}^{M} A(x^{(m)}) w(x^{(m)}) \\ &= \frac{\sum_{m=1}^{M} A(x^{(m)}) w(x^{(m)})}{\sum_{m=1}^{M} w(x^{(m)})}\end{align}
アルゴリズム的には、提案分布\(q(x)\)からサンプリングを行い、重要度重みと統計量の重要度重み付き和を計算すれば良いです。
ここまでの結果を含め、アルゴリズムを整理します。
重点サンプリングのアルゴリズム
重点サンプリングのアルゴリズム
- \(q(x)\)からサンプル\((x^{(m)})_{m=1, \ldots M}\)を生成
- 各サンプルに対して、重み\(w(x^{(m)})\)と統計量\(A(x^{(m)})\)を計算
得られた重み\((w^{(m)})_{m=1, \ldots, M}\)と統計量\((A(x^{(m)}))_{m=1, \ldots, M}\)を用いて以下を計算する
- 期待値
$$\mathbb{E}_{p}[A(x)] \approx \frac{\sum_{m=1}^{M} A(x^{(m)}) w(x^{(m)})}{\sum_{m=1}^{M} w(x^{m})}$$
- 規格化定数
$$Z_{p} \approx \frac{Z_{q}}{M} \sum_{m=1}^{M} w(x^{(m)})$$
この後は、このアルゴリズムをPythonで実装して挙動を確かめます。
重点サンプリングの具体例（Python）
ここでは、実際にPythonを用いて重点サンプリングを実装していきます。
今回使用する例は以下の一次元混合ガウス分布です。
$$\pi \mathcal{N}(0, 1) + (1- \pi) \mathcal{N}(4, 1)$$
重点サンプリングの設定では、規格化されていない確率分布が既知という状況なので、以下の関数のみ既知であることを仮定します。
このような状況下で平均と規格化定数\(Z\)を推定する問題を考えます。
今回は、正解が計算できて、平均は\(4\)となり、規格化定数\(Z\)は、\(\sqrt{2 \pi}\)となります。
提案分布をガウス分布として、以下の二つのガウス分布を用いて挙動を確かめます。
- 提案分布1 : \(\mathcal{N}(0, 1)\)
- 提案分布2 : \(\mathcal{N}(2, 4)\)
使用するライブラリをインポート
まずは、以下のように実装に使用するライブラリをインポートしてください。
import numpy as np
from matplotlib import pyplot as plt
# SEEDを固定
np.random.seed(0)
混合ガウス分布と提案分布を定義
まずは、規格化されていない混合ガウス分布とガウス分布を定義しておきます。
# target
def f(x, mu1=0.0, mu2=4.0, pi=0.5):
pi1 =pi
pi2 =1-pi1
a1 = - ((x - mu1)**(2)) / 2
a2 = - ((x - mu2)**(2)) / 2
return pi1*np.exp(a1)+pi2*np.exp(a2)
# proposal
def g(x, mu=0, scale=1):
return np.exp(-((x - mu)**2)/(2*(scale**2)))
定義した関数を用いて、ターゲットとなる混合ガウス分布と提案分布をプロットしてみましょう。
x=np.linspace(-10.0, 10.0, 1000)
fig, ax = plt.subplots(figsize=(16, 9))
ax.plot(x, f(x), linewidth=3, label='target dist')
ax.plot(x, g(x, mu=0, scale=1), linestyle='--', linewidth=3, label=r'proposal dist1 : $\mu=0, \sigma=1$')
ax.plot(x, g(x, mu=2, scale=2), linestyle='--', linewidth=3, label=r'proposal dist2 : $\mu=2, \sigma=2$')
plt.legend(fontsize=17)
plt.tick_params(axis='y', labelsize=20)
plt.tick_params(axis='x', labelsize=20)
plt.show()
<output>
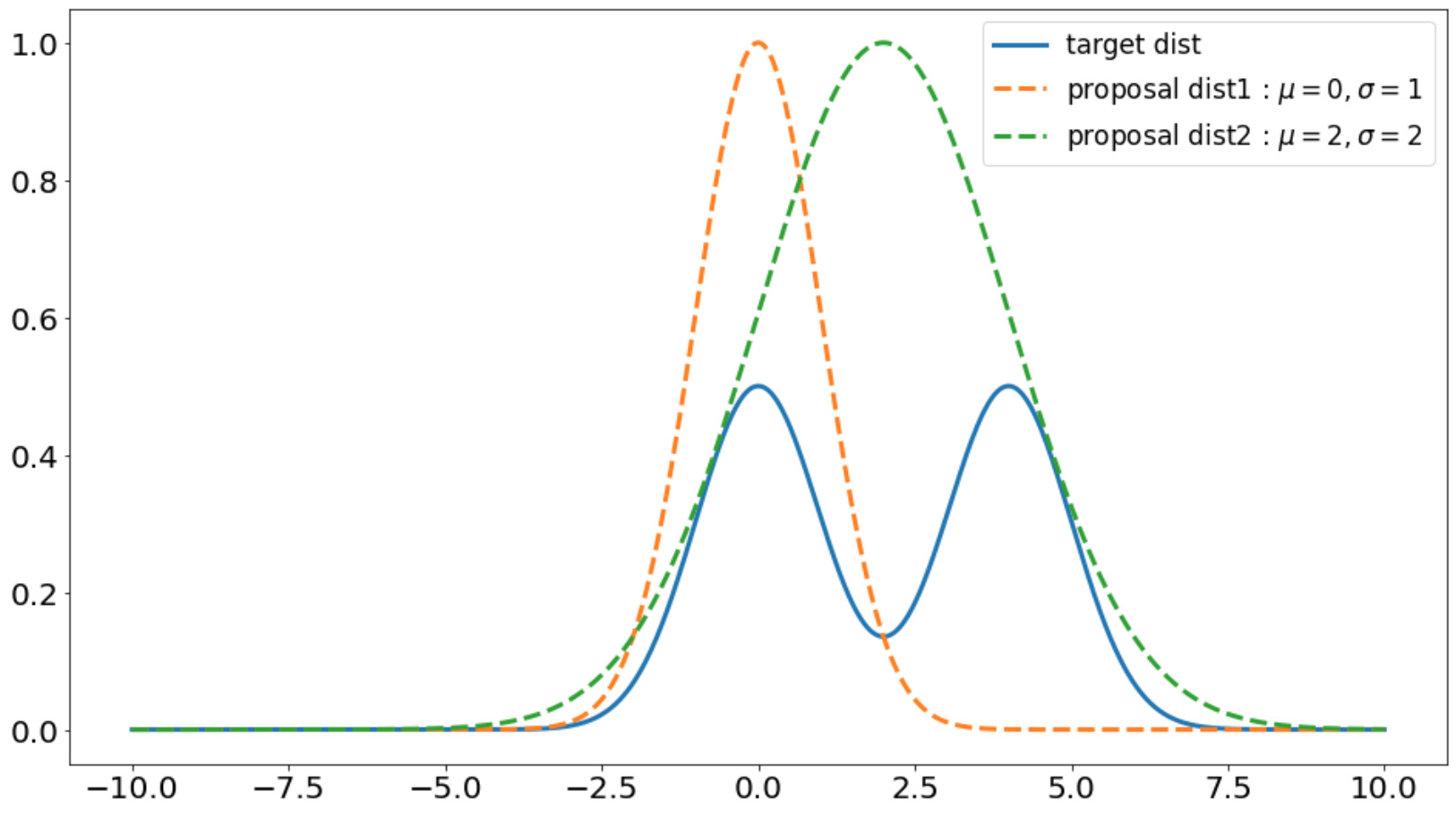
提案分布2（\(\mathcal{N}(2, 4)\)）の方が目的となる確率分布\(p\)を全体的に覆っているのがわかります。
重点サンプリングのアルゴリズム
重点サンプリングのアルゴリズムを以下に示します。
def importance_sampling(n_samples=100, prop_mean=0, prop_scale=1):
'''重点サンプリング(Target : 多変量ガウス分布, 提案分布: ガウス分布)
Parameters
--------------
num : 提案分布から得るサンプル数
prop_mean : 提案分布(ガウス分布)の平均
prop_scale : 提案分布(ガウス分布)の標準偏差
Returns
---------
norm_term : 規格化定数の推定値
mean : 平均の推定値
'''
# 提案分布からのサンプル
samples = np.random.normal(loc=prop_mean, scale=prop_scale, size=n_samples)
# weightの計算
weights = f(samples)/g(samples, mu=prop_mean, scale=prop_scale)
# 規格化定数
norm_term = (np.sum(weights)/n_samples)*np.sqrt(2*np.pi*(prop_scale**2))
# 平均
mean = np.sum(samples*weights)/weights.sum()
return norm_term, mean
先ほど説明した平均\(0\), 標準偏差\(1\)のガウス分布と平均\(2\), 標準偏差\(2\)のガウス分布のケースでアルゴリズムの結果を示していきます。
重点サンプリングの結果
今回は、重点サンプリングによって得られた規格化定数と平均から真の値を引いた値のサンプル数依存性を確かめます。
各サンプルごとの重点サンプリングは以下のコードで実行できます。
loss_norms1, loss_norms2 = [], []
loss_means1, loss_means2 = [], []
for i in range(1, 5000, 10):
norm_term1, mean1 = importance_sampling(n_samples=i, prop_mean=0, prop_scale=1)
norm_term2, mean2 = importance_sampling(n_samples=i, prop_mean=2, prop_scale=2)
loss_norm1 = norm_term1- np.sqrt(2*np.pi)
loss_norm2 = norm_term2- np.sqrt(2*np.pi)
loss_mean1 = mean1 - 2
loss_mean2 = mean2 - 2
loss_norms1.append(loss_norm1)
loss_norms2.append(loss_norm2)
loss_means1.append(loss_mean1)
loss_means2.append(loss_mean2)
ここで、リストは以下を格納しています。
- 『loss_norm1』、『loss_mean1』 : \(q(x)\)として平均\(0\)、標準偏差\(1\)のガウス分布を利用した結果
- 『loss_norm2』、『loss_mean2』 : \(q(x)\)として平均\(2\)、標準偏差\(2\)のガウス分布を利用した結果
得られた規格化定数の結果をプロットします。
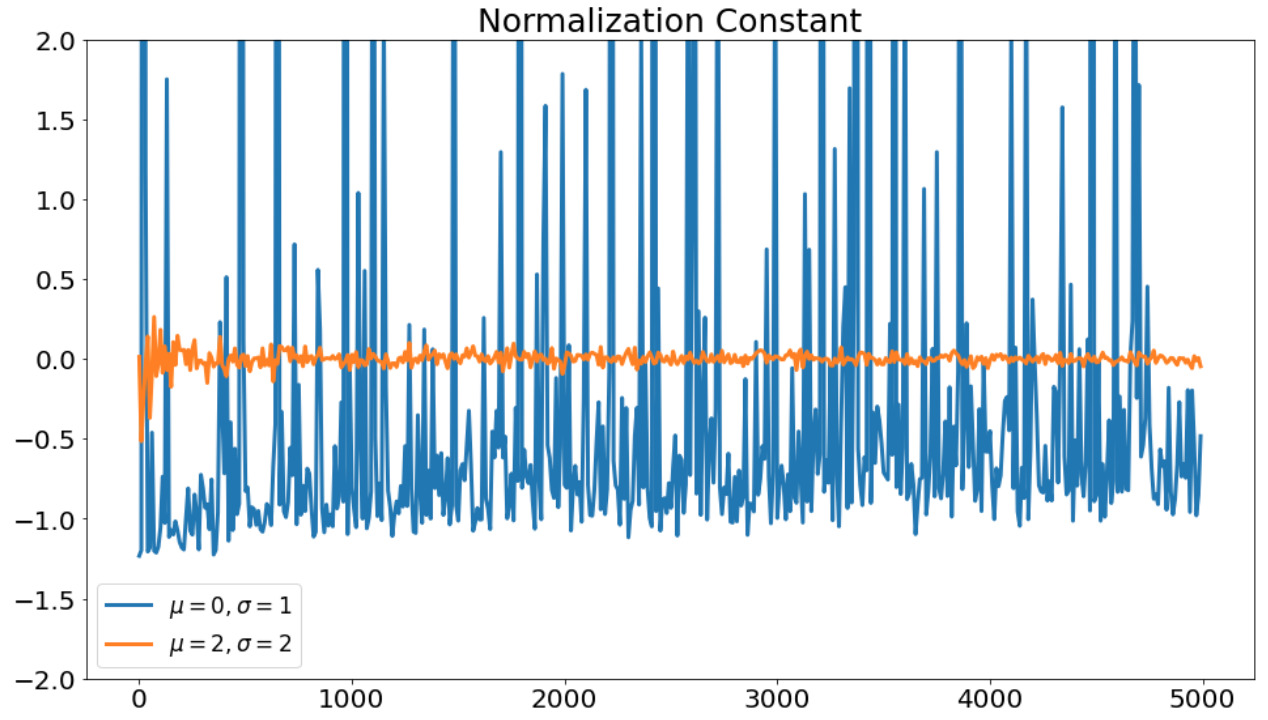規格化定数の推定結果。横軸は重点サンプリングで使用したサンプル数を表す。
次に平均の推定結果を示します。
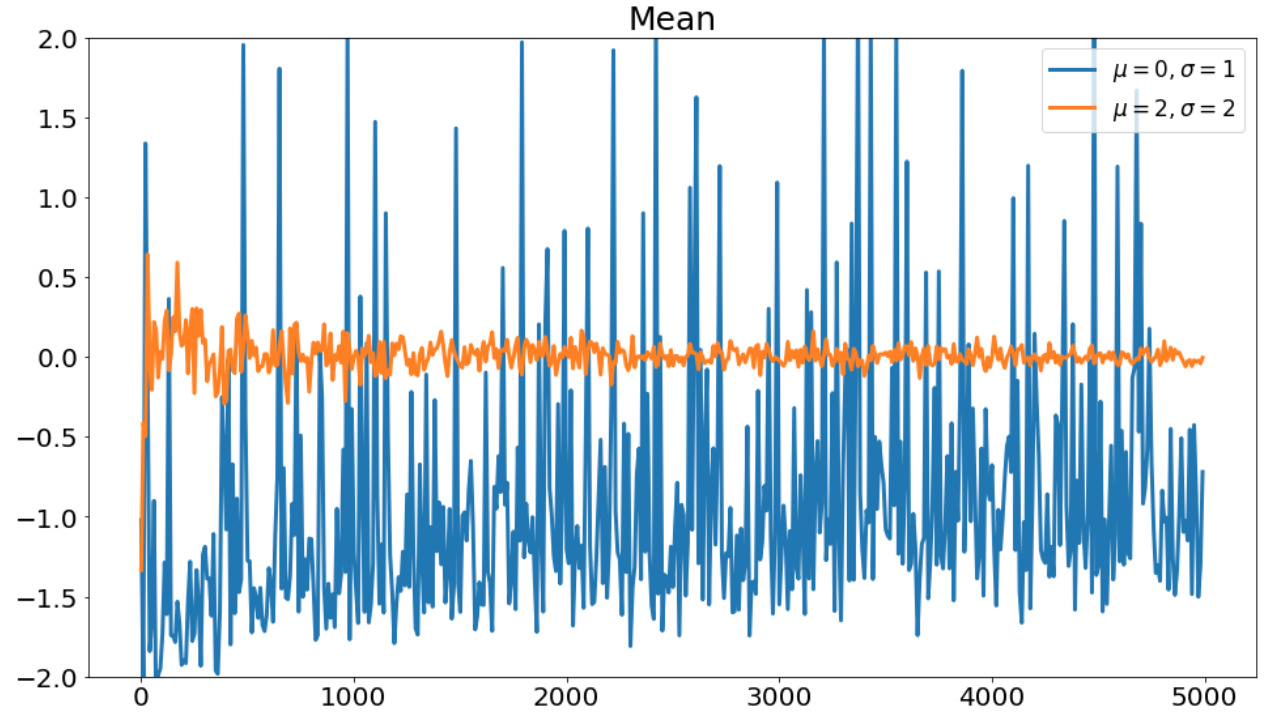平均の推定結果。横軸は重点サンプリングのサンプル数を表す。
分布\(q(x)\)が似ている分布でないと正しい推定結果が得られていないことがわかります。
実は、分布\(q(x)\)が似ていない場合は、重要度重みの分散が大きくなり、推定精度が悪くなってしまいます。
実際、各提案分布に対して重みの分散を評価すると以下のようになります。
def eval_weight(n_samples=100, prop_mean=0, prop_scale=1):
samples = np.random.normal(loc=prop_mean, scale=prop_scale, size=n_samples)
# weightの計算
weights = f(samples)/g(samples, mu=prop_mean, scale=prop_scale)
return weights
weights1 = eval_weight(n_samples=5000, prop_mean=1, prop_scale=1)
weights2 = eval_weight(n_samples=5000, prop_mean=2, prop_scale=2)
print(f'【weight variance】 proposal dist1 : {weights1.var():.3f}, proposal dist2 : {weights2.var():.3f} ')
<output>
【weight variance】 proposal dist1 : 1440.412, proposal dist2 : 0.089
このように形状が類似していない提案分布1の場合、重みの分散が大きくなっています。
まとめ
本記事では、重点サンプリングの理論とPythonによる実装を紹介しました。
皆さんも本記事で紹介したコードのパラメータを変えて遊んでみてください。
Pythonを学習するのに効率的なサービスを紹介していきます。
まず最初におすすめするのは、Udemyです。
Udemyは、Pythonに特化した授業がたくさんあり、どの授業も良質です。
また、セール中は1500円定義で利用することができ、コスパも最強です。
下記の記事では、実際に私が15個以上の講義を受講して特におすすめだった講義を紹介しています。
他のPythonに特化したオンライン・オフラインスクールも下記の記事でまとめています。
自分の学習スタイルに合わせて最適なものを選びましょう。
また、私がPythonを学ぶ際に使用した本を全て暴露しているので参考にしてください。
