【Python】棄却サンプリングの実装と理論
本記事では、マルコフ連鎖を利用しないモンテカルロ法(静的なモンテカルロ法)の一つである『棄却サンプリング』について説明します。
また、理解度を高めるためにPythonの実装例を本記事の後半に示します。
棄却サンプリング(Rejection Sampling)の解説

まずは、棄却サンプリング(Rejection Sampling)の基本知識を説明していきます。
棄却サンプリングの設定
棄却サンプリングの目的は、サンプリングしたい確率分布\(p(x)\)の規格化定数が未知ですが、規格化されていない\(\tilde{p}(x)\)は簡単に計算できる状況で、確率分布\(p(x)\)からサンプリングを行うことです。
すなわち以下のような確率分布で、\(\tilde{p}(x)\)は既知ですが規格化定数\(Z\)は未知という状況です。
$$p(x) = \frac{1}{Z} \tilde{p}(x),~~~Z = \int p(x) dx$$
棄却サンプリングのアルゴリズム
まず、棄却サンプリングでは、任意の\(x\)に対して以下の条件を満たし、サンプリングが容易な提案分布\(q(x)\)を選択します。
$$kq(x) \ge \tilde{p}(x)$$
すなわち、\(kq(x)\)が\(p(x)\)の全てを覆う状況を意味しています。
このような提案分布を用いて、棄却サンプリングは以下のプロセスで確率分布からサンプリングを行います。
- \(q(x)\)から、\(x_{i}\)を生成
- 区間\([0, kq(x_{i})]\)の一様分布から乱数\(u_{i}\)を生成
- \(u_{i} \le \tilde{p}(x_{i})\)ならばサンプルを受理、\(u_{i} > \tilde{p}(x_{i})\)ならサンプルを棄却
③で受理したサンプルは\(p(x)\)に従うことを簡単に示すことができます。
棄却サンプリングの実装(Python)

ここからは、棄却サンプリングを実装していきましょう。
まずは、使用するライブラリをインポートしてください。
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
plt.style.use('seaborn-dark')
np.random.seed(0)
サンプリングを目指す確率分布について
今回は以下の混合ガウス分布からのサンプリングを目指します!
$$p(x \mid \mu_{1}, \mu_{2}, \sigma_{1}^{2}, \sigma_{2}^{2}, \pi_{1}, \pi_{2}) = \pi_{1} \mathcal{N}(x \mid \mu_{1}, \sigma_{1}^{2}) + \pi_{2} \mathcal{N}(x \mid \mu_{1}, \sigma_{1}^{2})$$
ここで、\(\pi_{1}, \pi_{2}\)は、\(\pi_{1} + \pi_{2}\)を満たします。
棄却サンプリングでは、規格化定数が未知の状態でのサンプリングを行う手法なので、規格化されていない混合ガウス分布を以下のように定義します。
\begin{align}&\tilde{p}(x \mid \mu_{1}, \mu_{2}, \sigma_{1}^{2}, \sigma_{2}^{2}, \pi_{1}, \pi_{2}) \\ = &\pi_{1} \exp \left(-\frac{(x – \mu_{1})^{2}}{2 \sigma_{1}^{2}} \right) + \pi_{2} \exp \left(-\frac{(x – \mu_{1})^{2}}{2 \sigma_{1}^{2}} \right) \end{align}
規格化された分布と規格化されていない分布を以下にプロットします。
# Mixed Gaussian
def mgauss_target(x, mu1=2.0, mu2=-2.0, scale1=1.0, scale2=1.0, pi=0.5):
pi1 =pi
pi2 =1-pi1
return pi1*stats.norm.pdf(x, loc=mu1, scale=scale1)+pi2*stats.norm.pdf(x, loc=mu2, scale=scale2)
# unnormalized Mixed Gaussian
def mgauss(x, mu1=2.0, mu2=-2.0, scale1=1.0, scale2=1.0, pi=0.5):
pi1 =pi
pi2 =1-pi1
a1 = - ((x - mu1)**(2)) / (2*scale1**(2))
a2 = - ((x - mu2)**(2)) / (2*scale2**(2))
return pi1*np.exp(a1)+pi2*np.exp(a2)
x=np.linspace(-10.0, 10.0, 1000)
fig, ax = plt.subplots(figsize=(16, 9))
ax.plot(x, mgauss(x), linewidth=3, label='unnormalized gaussian mixture')
ax.plot(x, mgauss_target(x), linewidth=3, label='normalized gaussian mixture')
plt.legend(fontsize=17)
plt.tick_params(axis='y', labelsize=20)
plt.tick_params(axis='x', labelsize=20)
plt.show()
<output>
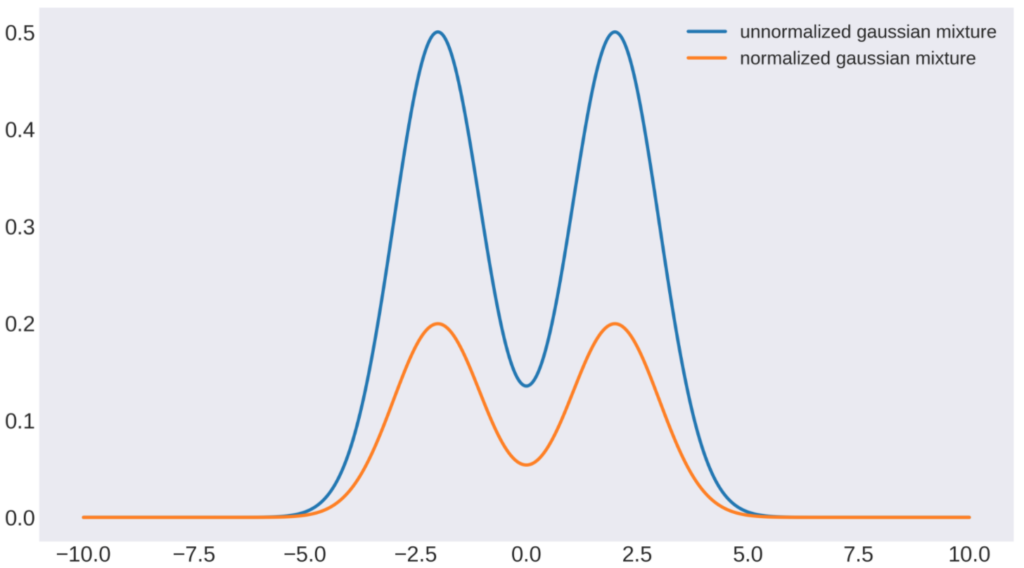 青色が規格化されていない分布で、オレンジ色が規格化された分布
青色が規格化されていない分布で、オレンジ色が規格化された分布
提案分布の設定
今回棄却サンプリングに使用する提案分布は、以下のガウス分布です。
$$q(x) = \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}} \right)$$
まずは、\(q(x)\)が\(\tilde{p}(x)\)にぎりぎり覆い被さるような\(k\)を計算して、棄却サンプリングを実装します。
# 提案分布
def q(x, loc=0, scale=1):
return stats.norm.pdf(x, loc=loc, scale=scale)
x = np.linspace(-10.0, 10.0, 500)
# 最適なkを計算
k_opt = np.max(mgauss(x)/q(x, scale=2))
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, mgauss(x), linewidth=3, label='unnormalized gaussian mixture')
ax.plot(x, k_opt*q(x, scale=2), linewidth=3, label='normalized gaussian')
plt.legend(fontsize=13)
plt.tick_params(axis='y', labelsize=20)
plt.tick_params(axis='x', labelsize=20)
plt.show()
<output>
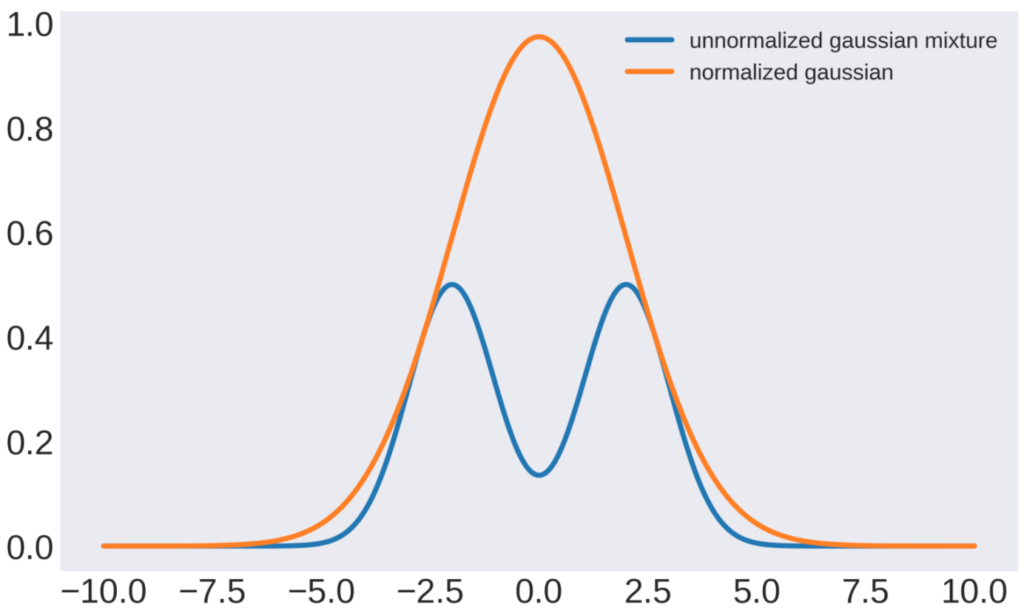 黄色が提案分布で青色が規格化されていない混合ガウス分布
黄色が提案分布で青色が規格化されていない混合ガウス分布
棄却サンプリングのアルゴリズム
いよいよ、棄却サンプリングアルゴリズムを実装します。
実装は以下のようになります。
def rejection_sampling(times=100, k=k_opt):
'''Rejection Sampling
Parameters
times : 使用するサンプル数
k : Rejection Samplingの条件を満たすようなk
Return
samples : acceptされたサンプル
'''
samples = []
accepted_num = 0
for i in range(times):
x = np.random.normal(0, 2.0)
u = np.random.uniform(0, k*q(x, scale=2))
if u <= mgauss(x):
samples.append(x)
accepted_num += 1
print(f'ACCEPTANCE RATE : {accepted_num/times}')
return samples, accepted_num/times
棄却サンプリングの結果
棄却サンプリングで得られた結果と規格化されている混合ガウス分布を比較してみました。
samples = rejection_sampling(times=10000)
fig, ax = plt.subplots(figsize=(16, 9))
ax.hist(samples, bins=50, density=True, label='accepted sample')
ax.plot(x, mgauss_target(x), linewidth=3, label='unnormalized gaussian mixture')
plt.legend(fontsize=17)
plt.tick_params(axis='y', labelsize=20)
plt.tick_params(axis='x', labelsize=20)
plt.show()
<output>
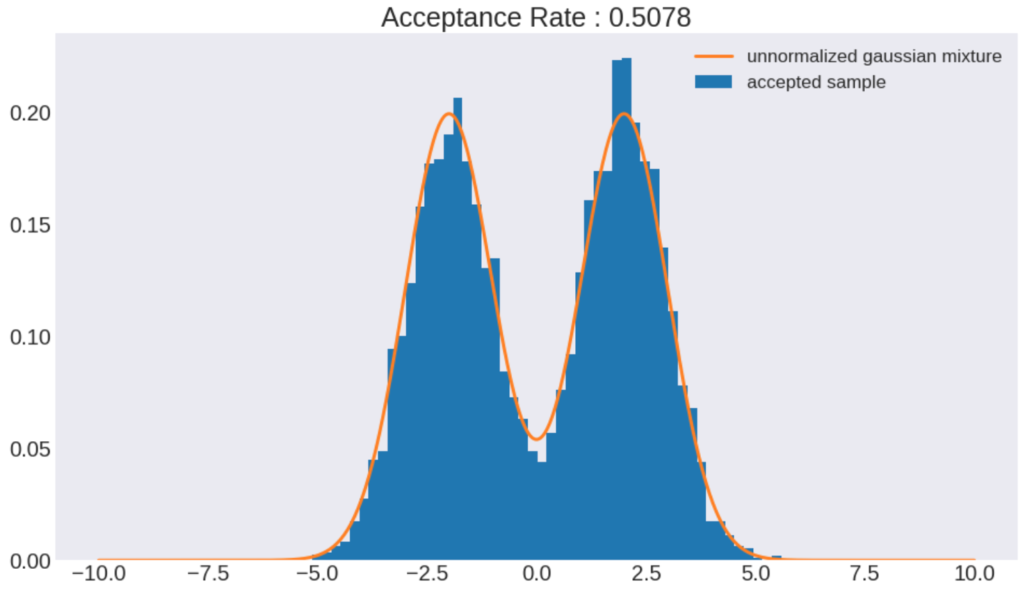
分布の形状の類似度と受理率の関係
以下のように、\(k\)の値を大きくして分布の類似度を小さくした場合、受理されるサンプル挙動を確認してみます。
まず、\(k\)を変えた時の様子を以下にプロットします。
x = np.linspace(-10.0, 10.0, 500)
fig, ax = plt.subplots(figsize=(10, 6))
ax.plot(x, mgauss(x), linewidth=3, label='target')
for k in ks:
ax.plot(x, k*q(x, scale=2), linewidth=3, label=f'k = {k:.1f}')
plt.legend(fontsize=13)
plt.tick_params(axis='y', labelsize=20)
plt.tick_params(axis='x', labelsize=20)
plt.show()
<output>
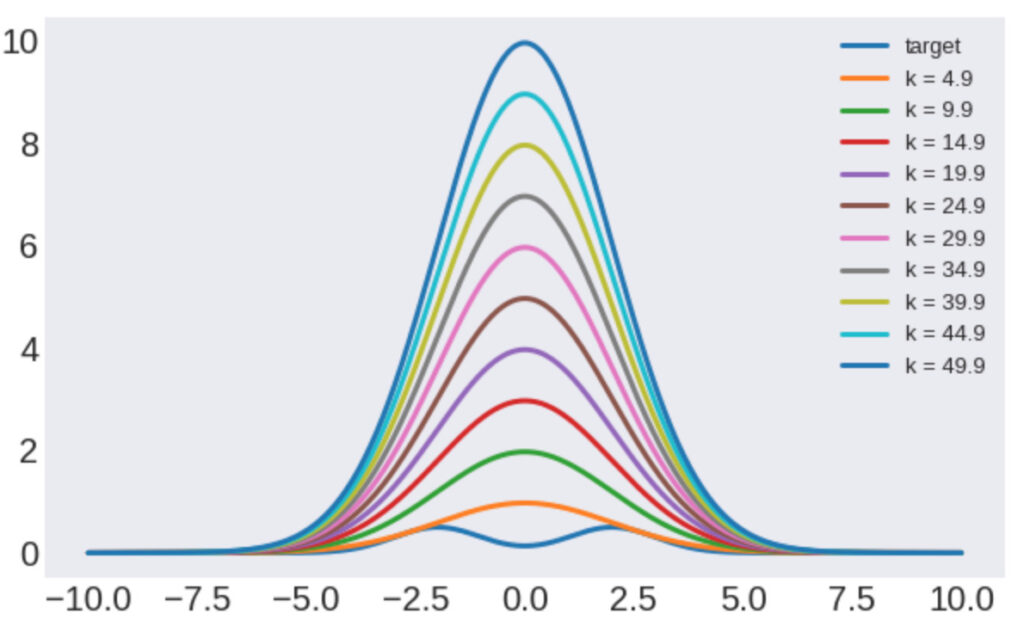
次に棄却サンプリングの受理確率と\(k\)の関係を以下に示します。
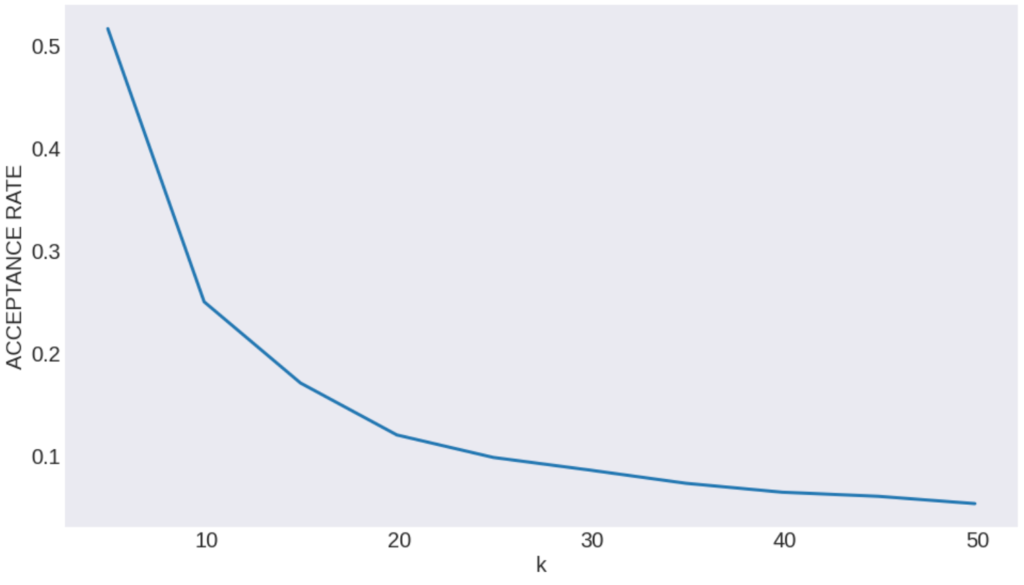
この結果から分かるように、提案分布とサンプリングしたい確率分布の類似度が小さいと受理されるサンプル数が大幅に減少します…
低次元の場合は、簡単に類似度の高い分布を見つけることができますが、高次元になると簡単に類似度が高い分布を見つけることができません。
その結果、次元が高くなるにつれて、受理されるサンプル数が大幅に減少してしまい、高次元で棄却サンプリングを使用するのは困難となります。
まとめ
本記事では棄却サンプリングを利用して、規格化定数が未知の確率分布からサンプリングする方法を紹介しました。
後半では、具体例を示すため、Pythonによる実装をまとめました。

『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。