テンソル積・直積・直和をわかりやすい具体例で徹底解説

物理で出てくる直積・直和が解らない…
線形代数の本を読んだけど、結局よく解らない…
量子力学の複合状態がわからない…

本記事では、その悩みを解決していきます。

実は、直積・直和は数学のカテゴリ（例えば、代数学や集合論など）ごとに違う意味を持っています。

特に本記事では、線形代数で出てくる直積と演算ルールとしての直積を紹介します。

その中で、物理によく出てくる直積・直和は、線型空間という要素が特定のルールをもった集合に対する直積・直和です（量子力学に出てきます）

『線型空間…』という方もいると思うので、本記事では線形代数の基本を簡単に説明してから直積・直和を説明していきます。

なるべく抽象的な表現を避け、どんなレベルの方でも理解できるようにまとめていきます。

本記事を読むメリット

線形代数が怪しくても、直積・直和が理解できる

本記事を読んでわからないことや質問があったらTwitterのDM（努力のガリレオのTwitterはこちら）または、コメント欄でコメントください。

＊（iphone・Androidの方へ）数式はスクロール可能です。

直積・直和を理解するために準備
直和と直積（ベクトル空間）
- 和空間・直和とは
- 直積とは
演算としての直積（テンソル積）
テンソル積と量子力学
まとめ

直積・直和を理解するために準備

まず、直積・直和を理解するためには、線形代数の基本を理解する必要があります。

これから説明する内容は、やや公理的な話になります。

しかし、直積・直和を理解するためには必要最低限の知識になるので頑張ってついてください。

『これから紹介する内容が全くわからない…』という方は、下記を参考にしてください

【院試対策】確実に力がつく線形代数の参考書10選

ベクトル空間（線型空間）

高校数学の知識から、空間と聞くと図形的なイメージを思い浮かべるかもしれませんが、大学の数学で空間とは、『ある性質を満たす集合』を意味します。

そして、ある集合$V$の元に対して、以下の性質が成り立つ時、集合$V $を「ベクトル空間（線型空間）」といいます。

定義 : ベクトル空間

集合$V$の各元$ \mathbf{u},\mathbf{v}, \mathbf{w} \in V $、スカラー$ a, b \in \mathbb{R} $に対して以下が成り立つとき、$V$をベクトル空間という。

$\mathbf{u} + (\mathbf{v} + \mathbf{w}) = (\mathbf{u} + \mathbf{v}) + \mathbf{w} $
$\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}$
$ \mathbf{0} + \mathbf{u} = \mathbf{u} + \mathbf{0} = \mathbf{u} $となる零ベクトル$\mathbf{0} \in V$が存在する
$ \mathbf{u} + \mathbf{u^{\prime}} = 0 $となる逆元$\mathbf{u^{\prime}}$が存在する
$a (\mathbf{u} + \mathbf{v}) = a \mathbf{u} + a \mathbf{v}$
$ (a + b) \mathbf{u} = a \mathbf{u} + b \mathbf{u} $
$a(b \mathbf{v}) = (ab) \mathbf{v}$
$ 1 \mathbf{u} = \mathbf{u} $

ベクトル空間（線型空間）聞いて、嫌気がさした方もいるかもしれませんが、『各元が上記の性質を満たすような集合』というだけです。

実は、今までに学習してきた平面ベクトル・空間ベクトルも、ベクトル空間に含まれます。

一次結合

さらに、一次結合を導入しておきます。

定義 : 一次結合

あるベクトル$\mathbf{a}_{1}, \ldots, \mathbf{a}_{n}$、スカラー$x_{1}, \ldots, x_{n}$に対して、以下を一次結合という。

$$x_{1} \mathbf{a}_{1} + x_{2} \mathbf{a}_{2} + \cdots + x_{n} \mathbf{a}_{n}$$

1次独立・1次従属

ベクトル空間が定義されたので、その空間に関する重要な性質を紹介します。

まずは、１次独立・１次従属という性質です。

定義 : 一次独立・一次従属

$ {\bf a}_{1}, {\bf a}_{2}, \dots, {\bf a}_{n} \in {\bf V} $の一次結合に対する方程式を考える。

$$x_{1} {\bf a}_{1} + x_{1} {\bf a}_{1} + \cdots + x_{1} {\bf a}_{1} = 0 $$

$x_{1} = \cdots = x_{n} = 0 $のみが解のとき、$ {\bf a}_{1}, {\bf a}_{2}, \dots, {\bf a}_{n} $は一次独立という
$x_{1} = \cdots = x_{n} = 0 $以外の解が存在するとき、$ {\bf a}_{1}, {\bf a}_{2}, \dots, {\bf a}_{n} $は一次従属という

基底

一次独立が理解できていれば、基底の定義は難しくないので定義を書いてしまいます。

定義 : 基底

ある集合$V$のベクトルの組み$\{{\bf x}_{1}, {\bf x}_{2}, \ldots, {\bf x}_{d} \} $に対して、以下の２つの性質を満たすとき、そのベクトルの集合を$V$の基底という。

$ \{{\bf x}_{1}, {\bf x}_{2}, \ldots, {\bf x}_{d} \} $のベクトルの組みが一次独立
$V$の任意のベクトルが$ \{{\bf x}_{1}, {\bf x}_{2}, \ldots, {\bf x}_{d} \} $の一次結合で表現できる（生成系）

つまり基底とは、空間$V$からベクトルの組みを取り出して、そのベクトルが一次独立で$V$内のベクトルをその線形和で全て表せるようなものということですね。

基底の選び方はさまざまなものがありますが、基底の個数は一定となることが示せます。

一番簡単な具体例は、二次元空間上の$ {\bf e}_{1} = (1, 0),~{\bf e}_{2} = (0, 1) $です。

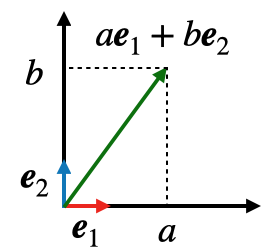
また、具体例のように基底の長さを１としたものを標準基底と呼びます。

次元

ここで定義される次元というのは、皆さんが想像する物理の次元という意味ではなく、ベクトルの次元を表します。

そして、ベクトル空間の次元は、「基底の数」で定義されます。

そして、あるベクトル空間$V$の次元は、$\mathrm{dim}V $と表されます。

一つのベクトル空間に対して、基底の選び方は任意性がありますが、基底を構成するベクトルの数は変わりません。（証明は省略）

部分ベクトル空間

あるベクトル空間の部分集合 $ W \subset V $ となっていて、$W$もベクトル集合になっているような集合を『$ {\bf V} $の部分空間』と呼びます。

形式的に定義しておきます。

定義 : 部分ベクトル空間

$V$をベクトル空間として、$W \subset V$とする。そして、以下が成り立つとき、$W$を部分ベクトル空間という。

$\mathbf{u}, \mathbf{v} \in W $ならば、$\mathbf{u} + \mathbf{v} \in W$となる
$k \in \mathbb{R}$, $\mathbf{u} \in W$ならば、$k\mathbf{a} \in W$

直和と直積（ベクトル空間）

ここからは、準備が整ったので集合論的な直和と直積について説明します

抽象的すぎないように、簡単な例で説明していきます。

和空間・直和とは

以下、二つの部分空間 $ W_{1} $, $ W_{2} $を考えます。

和空間とは、$ W_{1} $と$ W_{2} $の元の和で表される全てのベクトルからなる集合で以下のように定義されます。

$$ W_{1} + W_{2} \equiv \{ \mathbf{u} = \mathbf{u}_{1} + \mathbf{u}_{2} | \mathbf{u}_{1} \in W_{1} , \mathbf{u}_{2} \in W_{2} \} $$

つまり、部分空間 $ W_{1} $, $W_{2} $の基底ベクトルの線形和で表現できるできる集合が和空間を意味します。

（直交）直和空間とはさらに制限を強くしたもので以下のように定義されます。

$ W_{1} \cap W_{2} = \{ 0\} $かつ$ W_{1} $ と $ W_{2} $の任意の元が直交するような和空間を（直交）直和空間といい以下のように表します。

$$ W_{1} \bigoplus W_{2} $$

また、直和空間の次元は、$ \dim(W_{1} + W_{2}) = \dim(W_{1}) + \dim(W_{2}) $となります。

直和空間は、実は対角化と関係してます。少し詳しく説明すると対角化は、ベクトル空間を直和空間に分解することです。

直積とは

直積は、直和と記号が似ていますが全く違う概念です。

前回と同様に、二つの部分空間$ W_{1} $ と $ W_{2} $ を使って考えます。

直積というのは、$ W_{1} $ の元$ \mathbf{u_{1}} $と $ W_{2} $の元$ \mathbf{u_{2}} $をペアにして、$ ( \mathbf{u_{1}}, \mathbf{u_{2}} ) $のように順序を決めて並べ、その要素列を元とする集合です。

直積空間$W$は、以下のような記号を使って表されます。

$$ W = W_{1} \times W_{2} $$

実は、そのような集合もベクトル空間になります（証明は省略）

実は、二次元座標系も実数全体の集合$ \mathbb(R) $の直積で、以下のように表現されます。

$$ \mathbb{R} \times \mathbb{R} $$

演算としての直積（テンソル積）

ここからは、演算としての直積（テンソル積）を解説していきます。

直積（テンソル積）とは、量子力学で見かける$\otimes$です。

直積（テンソル積）とは

これまでと同様に二つのベクトル空間$A_{1} $, $A_{2}$を考えます。

ここで、ベクトル空間$A_{1}$は、基底$\{\mathbf{e}_{i} \}_{i=1, \ldots, \dim A_{1}} $で表され、ベクトル空間$A_{2}$は、基底$\{\mathbf{e}_{j} \}_{j=1, \ldots, \dim A_{2}} $で表されるとします。

ベクトル空間$A_{1}$と$A_{2}$のテンソル積空間$A_{1} \otimes A_{2} $は、$\dim \left( A_{1} \otimes A_{2} \right) = \dim A_{1} \dim A_{2} $となり、以下のような基底をもつ空間です。

$$\{\mathbf{e}_{i} \otimes \mathbf{e}_{j} \mid i=1, \ldots \dim A_{1}, j=1, \ldots, \dim A_{2} \}$$

『むむむ…ちょっと抽象的でよくわからない』という方のために次の節では具体例を紹介します。

直積（テンソル積）の具体例

シンプルな具体例として、二つの基底で表すことができるようなベクトル空間$A_{1}, A_{2}$を用意します。

具体的には、$A_{1}$の任意の元は、二つの基底の線型結合$a_{1} \mathbf{e}_{1} + a_{2} \mathbf{e}_{2} $で表せ、$A_{2}$の任意の元もまた、二つの基底$a_{3} \mathbf{e}_{3} + a_{4} \mathbf{e}_{4} $で表すことができるとします。

このとき$A_{1}$と$A_{2} $のテンソル積集合$A_{1} \otimes A_{2} $の基底を考えましょう。

テンソル積集合は、各ベクトル空間$A_{1}$, $A_{2}$の基底を使って以下のように表せます。

$$ ( a_{1} \mathbf{e_{1}} + a_{2} \mathbf{e_{2}} ) \otimes ( a_{3} \mathbf{e_{1}} + a_{4} \mathbf{e_{2}} ) $$

テンソル積には分配法則が成り立つので、以下のように変形することができます（交換法則は成り立ちません）

$$ a_{1} a_{3} ~\mathbf{e}_{1} \otimes \mathbf{e}_{3} + a_{1} a_{4} ~\mathbf{e}_{1} \otimes \mathbf{e}_{4} + a_{2} a_{3}~ \mathbf{e}_{2} \otimes \mathbf{e}_{3} + a_{2} a_{4}~ \mathbf{e}_{2} \otimes \mathbf{e}_{4} $$

各係数を適当な定数に置き換えて見やすくすると以下のように表せます。

$$\tilde{a}_{1} ~\mathbf{e}_{1} \otimes \mathbf{e}_{3} + \tilde{a}_{2} ~\mathbf{e}_{1} \otimes \mathbf{e}_{4} + \tilde{a}_{3}~ \mathbf{e}_{2} \otimes \mathbf{e}_{3} + \tilde{a}_{4}~ \mathbf{e}_{2} \otimes \mathbf{e}_{4}$$

これは、テンソル積空間が、4つの基底$\{\mathbf{e}_{i} \otimes \mathbf{e}_{j} \mid i = 1, 2, j=3, 4\} $の線形和で表される空間ということを意味しています。

量子力学の場合、基底$\mathbf{e}_{1} \otimes \mathbf{e}_{2}$をケット表示という表示を使って$ |1\rangle \otimes |2 \rangle $と表記することが多いです。

さらに、$\otimes$を省略して、$ |1\rangle |2 \rangle $と表すこともあるので注意が必要です。

テンソル積の行列表記

テンソル積の結果を眺めていると行列で綺麗にまとめられそうなことに気がつきます。

具体的には、$ \mathbf{e_{1}} \otimes \mathbf{e_{1}} $ の係数を行列の要素に対応させると以下のような関係を得ることができます。

$$ \left( \begin{array}{c} a_{1} \\ a_{2} \end{array} \right) \otimes \left( \begin{array}{c} a_{3} \\ a_{4} \end{array} \right) = \left( \begin{array}{cc} a_{1} a_{1} & a_{1} a_{2} \\ a_{2} a_{1} & a_{2} a_{2} \end{array} \right) $$

この計算をよく見ると以下の行列演算で表現できますね。

$$ \left( \begin{array}{c} a_{1} \\ a_{2} \end{array} \right) \left( \begin{array}{cc} a_{3} & a_{4} \end{array} \right) = \left( \begin{array}{cc} a_{1} a_{1} & a_{1} a_{2} \\ a_{2} a_{1} & a_{2} a_{2} \end{array} \right) $$

テンソル積と量子力学

本章では、テンソル積が量子力学の中でどのように使用されるのかを解説していきます。

ざっくりと簡単に説明していきます（雰囲気を掴むことを最優先します）

詳しい内容を知りたい方は下記で紹介している量子力学の教科書を参考にしてください。

電子スピンはベクトルで表すことができる

皆さんご存知の電子は、原子の周りを回っているだけでなく、地球のように自転（スピン）しているのです。

さらに、その自転の状態を以下の二つの状態（基底）の線形結合で表すことができるのです。

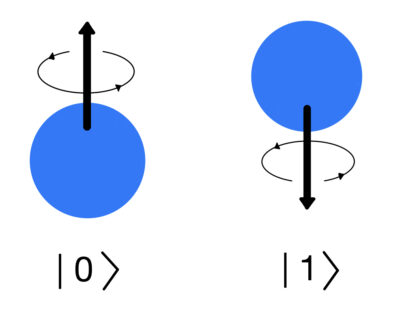
量子力学では、先ほど紹介したように基底をケット( $ | \cdots \rangle $ ）という記号を使って表します。

つまり、この二つの線形結合は以下のように表すことができます。

$$c_{1} | 1 \rangle + c_{2} | 2 \rangle $$

二つの電子の複合状態がテンソル積で表せる

二つの電子を複合系として見たときに、その複合系の基底はどのように表すことができるでしょうか？

実は、ここでテンソル積が活躍します。

ある電子スピンが$ c_{1} | 1 \rangle + c_{2} | 2 \rangle $で表され、もう一つの電子スピンが$ c_{3} | 3 \rangle + c_{4} | 4 \rangle $で表せるとき、二つの電子スピンの複合系の状態（基底）は以下のように表せます。

$$c_{1} | 1 \rangle + c_{2} | 2 \rangle \otimes c_{3} | 3 \rangle + c_{4} | 4 \rangle $$

さらに分配法則で整理すると以下のように表せます。

$$c_{1} c_{2} | 1 \rangle \otimes | 3 \rangle + c_{1} c_{3} | 1 \rangle \otimes | 3 \rangle + c_{2} c_{3} | 2 \rangle \otimes | 3 \rangle + c_{2} c_{4} | 2 \rangle \otimes | 4 \rangle$$

このような状態は、量子コンピュータや量子情報といった学問で頻繁に現れます。

クロネッカー積

もう一つ直積と呼ばれることがある演算としては、クロネッカー積という行列間の演算があります。

具体的には、以下のように定義されます。

直積（クロネッカー積）

$A = (a_{ij})$を$m_{1} \times n_{1}$型行列、$B = (b_{ij})$を$m_{2} \times n_{2} $行列とするとき以下で定義される$m_{1}m_{2} \times n_{1}n_{2}$型行列$A \otimes B$を$A$と$B$のクロネッカー積という。

$$A \otimes B = \left(\begin{array}{cccc} a_{11} B & a_{12} B & \cdots & a_{1n_{1}} B \\ a_{21} B & a_{22} B & \cdots & a_{2n_{1}} B \\ \vdots & \vdots & & \vdots \\ a_{m_{1} 1} B & a_{m_{1} 2} B & \cdots & a_{m_{1} n_{1}} B \end{array}\right)$$