【今度こそわかる】同相写像とは(定義・性質)
同相写像の理解は、多様体を理解するためには欠かせない基本知識です。
この記事では、数学的な厳密さを少し避けながら、同相写像について解説していきます。
同相写像を理解するための準備

まずは、同相写像を学ぶための準備をしていきます。
同相写像の準備
- 連続写像
- 逆写像
開集合・閉集合の理解を前提にしてく解説していきます。
『開集合…?』という方は下記を参考してください

同相写像の準備① 連続写像
具体的に、\(U\)、\(V\)をそれぞれ\(\mathbb{R}^{m} \)、\(\mathbb{R}^{m} \) の開集合とし、その写像\( f: U \rightarrow V \)を考えます。
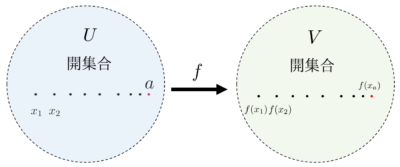
そして、\(U\)内の任意の点列\( \{ x_{n} \}_{n = 1}^{\infty} \) が以下の関係を満たす時に写像\( f: U \rightarrow V \) が点\(a \in U \)で連続であるといいます。
$$ \lim_{n \to \infty } x_{n} = n ~\Rightarrow~ \lim_{n \to \infty}f(x_{n}) = f(a) $$
\(f\)が\(U\)の各点で連続のとき、\(f\)を連続写像(continous map)といいます。
同相写像の準備② 逆写像
写像\( f : U \rightarrow V \)が全単射(全て元の写像が全て一対一対応)のとき、写像\(f\)の逆写像\( f^{-1} : V \rightarrow U \)を考えることができます。
皆さんの馴染みのある形で書くなら以下のように書くことができます。
写像\(f(x) = y \)のとき、逆写像\( f^{-1}(y) = x \)となります。
同相写像を理解する

ここからはいよいよ同相写像について解説していきます。
上述の同相写像を理解するための準備ができていれば確実に理解することができます
同相写像を理解する
- 同相写像の条件
- 同相写像の性質
- 座標表示
① 同相写像の条件
写像\(f:U \rightarrow V \)が以下の二つの条件を満たすとき、\(f\)を同相写像(homeomorphism)といいます。
- \(f : U \rightarrow V \)は全単射
- \(f: U \rightarrow V \)も\(f^{-1}:V \rightarrow U \)も共に連続写像
② 同相写像の性質
同相写像の条件から明らかですが、以下の二つの性質があります。
- \( f : U \rightarrow V \)が同相写像なら\(f^{-1} : V \rightarrow U \)も同相写像
- \(f : U \rightarrow V \)と\( g : V \rightarrow W \) が同相写像なら、\( g \circ f : U \rightarrow W \)も同相写像
また、\(U\)と\(V\)の間に同相写像\( f : U \rightarrow V \)があるとき、\(U\)と\(V\)は互いに位相同相(homeomorphic)といい以下のように書きます
$$ U \approx V $$
③ 座標表示
\(U\)、\(V\)をそれぞれ\(\mathbb{R}^{m} \)、\(\mathbb{R}^{m} \) の開集合とし、その写像\( f: U \rightarrow V \)を考えます。
このとき、\( x \in U \)の像\( f(x) \)は、\(f(x) = (y_{1}, y_{2}, \cdots, y_{n} ) \)のように\( \mathbb{R}^{m} \)の座標で書くことができます。
つまり、\( y_{i} \)は\(U\)上の関数になり以下のように書くことができます。
$$ y_{i} = f_{i}(x)~~~~( x \in U ) $$
この表記を使うと\( f(x) \)は以下のように書くことができます
$$ f(x) = ( f_{1}(x), f_{2}(x), \cdots f_{n}(x) ) = ( f_{1}, f_{2}, \cdots f_{n} ) $$
このような表し方を座標表示といいます。
教科書では略記され以下のように書かれることもあります
$$ f = (f_{1}, f_{2}, \cdots, f_{n} $$
参考資料
参考文献
まとめ
同相写像がイメージがなんとなくつかめましたか?
同相写像は多様体を理解するためには必要不可欠な知識です
今回の知識は必ず定着させておきましょう。
直積・直和の概念も必要不可欠です。
直積・直和について知りたい方は下記を参考にしてください


『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。