【勉強ノート】群論をわかりやすくまとめてみた
本記事は、群論の重要な定義・定理をまとめ、筆者並びに読者が頭を整理するように作成したノートです。
そのため、証明の大部分を省略し、群論の内容をサクッと整理できるようにすることに尽力しました。
もし、本記事を読んで『ほんとにこんな性質が成り立つの?』と思った方は本記事を読み終えてから専門書等で証明を行うことを進めます。
*はみ出ている数式はスクロールすることで全て見ることができます。
同値関係に関する基本知識のまとめ

群論を学ぶ上で、同値関係の理解は必須である。
そのため、同値関係の定義を簡単に学んでから群論のまとめを解説する。
すでに、以下の項目を学んだことがある方は読み飛ばしても良い。
- 二項関係
- 同値関係
- 同値類
- 商集合
二項関係
集合\(S\)上の二項関係とは、\(S \times S\)の部分集合\(R \subset S \times S\)である。
ある\(a, b \in S\)が考えている二項関係\(R\)に属するとき、\(a \sim b\)と表す(教科書によっては\(aRb\)と表すこともある)
同値関係
同値関係の定義について説明する。
同値関係
集合\(S\)上の二項関係\(R\)が以下の三つ条件を満たすとき、\(R\)が同値関係であるという。
- 反射律 : \(\forall a \in S,~~a \sim a\)
- 対称律 : \(\forall a, b \in S,~~a \sim b~\Rightarrow b \sim a\)
- 推移律 : \(\forall a, b, c \in S, a\sim b \wedge b \sim c \Rightarrow a \sim c \)
同値類
ある集合\(S\)と\(S\)における同値関係\(\sim\)に対して、以下を同値類という。
同値類(equivalence class)
$$C(a) = [a] = \{x \in S \mid a \sim x\}$$
また、同値類の要素を代表元(representative element)
さらに同値類に対して以下の定理が成立する。
定理1-1 : 任意の\(a, b \in S\)に対して以下は等価である。
- \(a \sim b\)
- \(C(a) = C(b)\)
- \(C(a) \cap C(b) \neq \emptyset\)
この同値類を集めたものが、次に説明する商集合である。
商集合
\(S\)の同値関係\(\sim\)による同値類全体の集合を商集合(quotient set)といい以下で定義する。
商集合(quotient set)
$$S\backslash{\sim} = \{C(a) \mid a \in S \}$$
定理1-1より、商集合の要素は互いに素なので\(S\)を異なる要素の直和で表せる。
$$S = \bigoplus_{C(a) \in S \backslash \sim} C(a)$$
一般に\(S\)を同値類の直和で表すことを類別(classification)という。
また、集合\(S\)から商集合\(S \backslash{\sim} \)への射影\(\pi : S \to S \backslash{\sim}\)を標準射影という。
この射影は、同値類の性質から明らかに全射である。
群論のまとめ

ここからは、群論の定義と定理を整理してく。
直感的に頭に残りやすいように、各定義と定理に可能なイメージ図を使用して説明する。
群の定義
まずは、群の定義について述べる。
群(group)
集合\(G\)に対して二項演算\(\cdot : G \times G \to G\)を定義し、\(\cdot\)が以下の三つの条件を満たすとき、\(G\)を群という。
- 結合法則 : \((a \cdot b) \cdot c = a \cdot (b \cdot c)\)
- 単位元の存在 :
\(\exists 1 \in G,~~\text{s.t.}~\forall a \in G,~a\cdot 1 = 1 \cdot a = a\)
- 逆元の存在 :
\(\forall a \in G,~~\exists a^{-1} \in G,~\text{s.t.}~a \cdot a^{-1} = a^{-1} \cdot a = 1\)
結合法則のみ成り立つ場合は半群といい、結合法則と単位元の存在が成り立つ場合は、モノイドという。
さらに以下が成り立つとき、\(G\)をアーベル群(Abelian group)という。
- 交換法則 : \(a \cdot b = b \cdot a\)
教科書等で、\(a \cdot b = ab\)と略して書くことがある。
また、群\(G\)の元の個数を\(G\)の位数といい、\(|G|\)で定義する。
例えば、\(\mathbb{Z}\)に対して、二項演算として加法\(+\)を導入すると、\(\mathbb{Z}\)は\(+\)に関して群を成す。
また、単位元と逆元に関して以下の定理が成り立つ。
定理2-1
- 単位元の一意性 : 群\(G\)に対して単位元はただ一つ存在する
- 逆元の一意性 : 任意の\(a \in G\)に対して逆元はただ一つ存在する
対称群
群の一つとして以下で定義される対称群がある。
対称群
以下の集合は、写像の合成を積として群になる。
一般に\(S_{n}\)を\(n\)次の対称群(symmetric group)といい、\(S_{n}\)の要素を置換(permutation)という。
\(S_{n}\)の単位元は恒等写像、逆元は逆写像となる。
また、\(\sigma \in S_{n}\)が任意の\(k \in \{1, \ldots, n\}\)に対して\(\sigma(k) = i_{k} \)と定められたとき、以下のように書き表す。
ここで、\(i_{1}, \ldots, i_{n}\)は\(1, \ldots, n\)の順列なので、\(|S_{n}| = n!\)となる。
部分群
群の部分集合で群の性質を満たすものを、部分群といい形式的には、以下で定義される。
部分群
\(H \subset G\)が以下を満たすとき\(H\)を部分群という。
- \(a, b \in H~ \Rightarrow~ ab \in H\)
- \(a \in H~ \Rightarrow~a^{-1} \in H\)
また、\(a \in H\)に対して、\(G\)の単位元\(1_{G} = a a^{-1} \in H\)となり、単位元の一意性から、\(H\)にも単位元が含まれることが示せる。
部分群\(H\)のイメージは以下に示す。
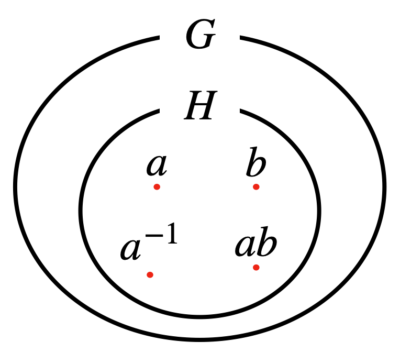 部分群のイメージ
部分群のイメージ
部分群に対して以下の定理が成立する。
定理2-2 : 群\(G\)、部分群\(H \subset G\)、\(g \in G\)に対して以下が成り立つ。
$$gH = H~ \Leftrightarrow ~ g \in H $$
ここで、\(gH\)を以下で定義した。
$$gH = \{gh \mid h \in H\}$$
剰余類
剰余類は以下で定義される。
剰余類(coset)
\(a \in G\)に対して、\(aH = \{ah \mid h \in H\}\)を\(a\)を含む\(H\)の左剰余類(left coset)といい、\(Ha = \{ha \mid h \in h\}\)を\(a\)を含む右剰余類(right coset)という。
さらに、同値関係\(a \sim b\)を\(aH = bH\)と定義する。
実際、\(aH = bH\)が同値関係の性質を満たすことは簡単に確かめることができる。
同値類を定義できたので、商集合\(G \backslash{\sim}\)を定義することができる。
一般に、\(aH = bH\)による商集合は、\(G \backslash{H}\)と表記されることが多い(右剰余類に関しても同値関係を定義すれば同様)
具体的には、\(G\backslash{H} = \{aH \mid a \in G\}\)を表している。
すると群\(G\)を以下のように表すことができる。
$$S = \bigoplus_{aH \in G\backslash{H}} aH$$
一般に、左剰余類と右剰余類は一致しないことに注意する。
しかし、群論では左剰余類と右剰余類が一致するような群が重要であり、以下ではそのようなケース(正規部分群)について解説する。
正規部分群
正規部分群とは以下のように定義される。
正規部分群(normal subgroup)
以下の条件を満たす部分群\(N \subset G\)を正規部分群という。
$$\forall a \in G,~~~aN = Na$$
定義から\(G\)がアーベル群の場合、任意の部分群は正規部分群という。
正規部分群であることをチェックするための以下の命題が成立する。
命題2-3 :
\(N \subset G\)が正規部分群であることは以下と等価である
$$\forall a \in G,~~a N a^{-1} \subset N$$
正規部分群の嬉しいポイントは、
任意の\(aN, bN \in G\backslash{N}\)に対して、以下のような二項演算を定義する。
$$(aN) \cdot (bN) \equiv abN$$
この演算は、代表元の撮り方によらないことが示せる(well-defined)。すなわち\(aN = a^{\prime} N\), \(bN = b^{\prime} N\)に対して、
この等式は、正規部分群でないと成り立たず、well-definedではない。
さらに、二項演算\((aN)(bN) = abN\)に対して\(G\backslash{N}\)は群の性質を満たし、剰余群(quotient group)と呼ばれる。
また、\(G\backslash{N}\)の単位元\(N\)で正規部分群自身となり、\(aN\)に対する逆元は\(a^{-1}N\)となる。
準同型・同型
準同型写像という概念を導入する。
準同型写像
\(f : G \to G^{\prime}\)が以下の性質を満たすとき、準同型写像(homomorphism)という。
$$f(g_{1} \cdot g_{2}) = f(g_{1}) \cdot^{\prime} f(g_{2})$$
この定義から、\(f(1_{G}) = f(1_{G}) = 1_{G^{\prime}}\)かつ\(f(g_{1}^{-1}) = f(g_{1})^{-1})\)が成り立つことが示せる。
この結果は、群\(G\)の単位元を準同型写像で飛ばしたときに、群\(G^{\prime}\)上で単位元となることを意味している。
ここまでの結果を可視化したものを以下に示す。
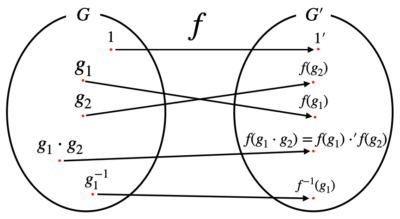 準同型写像のイメージ
準同型写像のイメージ
さらに、同型は以下で定義される。
同型(isomorphism)
\(f\)が準同型かつ全単射のとき、\(f\)を同型写像といい、\(G\)と\(G^{\prime}\)を同型(isomorphism)といい、\(G \simeq G^{\prime}\)で表す。
像(image)と核(kernel)
準同型写像\(f : G \to G^{\prime}\)に対して\(f\)による像と核を以下で定義する。
像(image)
\(\text{Im} \equiv \{f(g) \in G^{\prime} \mid g \in G \}\)を\(G\)の\(f\)による像(image)という
核(kernel)
\(\text{Ker}f \equiv \{g \in G \mid f(g) = 1^{\prime}\}\)を\(f\)の核(kernel)という
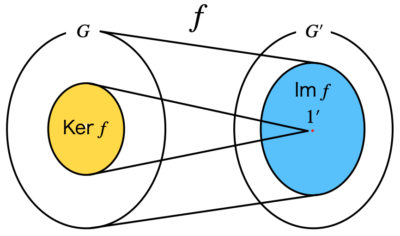 像(Image)と核(Kernel)のイメージ
像(Image)と核(Kernel)のイメージ
この核と像に対して以下の性質が成り立つ。
命題2-4:
- \(\text{Im} f\)は\(G^{\prime}\)の部分群
- \(\text{Ker} f\)は\(G\)の正規部分群
さらに以下の命題が成り立つ。
命題2-5 :
準同型写像\(f : G \to G^{\prime}\)に対して、\(f\)が単写であることと、\(\text{Ker} ~f = \{1\}\)は同値である。
準同型定理
群論で最も重要な準同型定理は以下のような主張である。
定理2-6 : 準同型定理
準同型写像\(f : G \to G^{\prime}\)に対して、\(\tilde{f} : G \backslash{\text{Ker}~f} \to \text{Im}~f\)を\(\tilde{f}(g \text{Ker}~f) \equiv f(g)\)と定めると、\(\tilde{f}\)は同型写像である。すなわち以下が成り立つ。
$$G \backslash{\text{Ker}~f} \simeq \text{Im}~ f$$
\(\tilde{f}\)は、\(\text{Ker}~f\)が正規部分群なのでwell-defiedになる。
準同型定理のイメージを以下に示す。
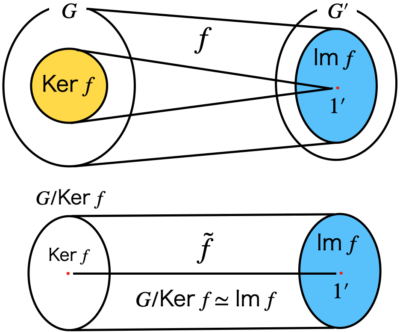 準同型定理のイメージ
準同型定理のイメージ
この定理を使うことで、二つの群の間の同型写像の具体的な構成方法を与える。
まとめ
群論の基本的な定義と定理をまとめました。
本記事では、証明をほとんど省き、群論の知識をまとめることに尽力し記事をまとめました。
一度も群論学んだことがない方は、本記事をサクッと読んだで『ほんとにそうなるの?』と思う部分を必ず手を動かして証明していください。

『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。