敵対的生成ネットワーク(GAN)の理論を解説
『敵対的生成ネットワーク(Generative adversarial network ; GAN)』は、生成モデルとして一躍有名になったモデルの一つです。
現在は、生成モデル以外にもさまざまな応用がなされています!
例えば、自動診断ための人工データ生成や機械翻訳などが挙げられます(それ以外にも数え切れないほどあります…)
理論的にも通常の機械学習と異なり、自分自身をより良いものに改善していくフィードバック構造を持ちます。
そのため、理論もとても斬新で面白いです。
その一部を伝えられたら良いと思い、本記事を作成しました。
敵対的生成ネットワーク(GAN)の目的
敵対的生成ネットワーク(Generative adversarial network ; GAN)は、学習データ\(\mathcal{D} = \{\mathbf{x}_{1}, \ldots, \mathbf{x}_{n} \}\)の生成過程を近似的に再現するモデルです。
より詳しく説明すると、学習データ\(\mathcal{D} = \{\mathbf{x}_{1}, \ldots, \mathbf{x}_{n} \}\)がある確率分布\(q(X)\)によって生成されることを仮定して、GANを用いてその確率分布を近似します。
以降、学習データの真の確率分布\(q(X)\)を『真の生成モデル』と呼び、GANを含め一般的に、データの生成過程を近似するモデルのことを生成モデルと分けて呼ぶことにします。
GANの基本的な構造
GANは、二つのモデルから構成されます。
具体的には、以下の目的を持つ二つのモデルです。
- Generator(生成機) : 本物のデータとそっくりな偽物のデータを生成する
- Discriminator(識別器): 本物のデータを偽物のデータと見分ける
この二つのモデルがお互いを出し抜くように学習します。
このことが、GANの名前の『Adversarial(敵対的)』の由来になっています。
GANで使用するモデルを定義
まずは、GeneratorとDiscriminatorという二つのネットワークを形式的に定義します。
定義: Generator・Discriminator
- Generator : \( G : \mathcal{Z} \to \mathcal{X} \)
- Discriminator : \( D : \mathcal{X} \to \mathbb{R} \)
ここで、\(\mathcal{X}\)は、データ\( \mathbf{x} \in \mathcal{X} \)の空間、\(\mathcal{Z}\)は、私たちが設定する適当な空間(潜在空間)とする。
Discriminatorの役割は先ほど述べたように、偽物のデータと本物のデータを見分けることです。
そのため、Discriminatorの出力\(D(\mathbf{x})\)は、\(\mathbf{x}\)が本物である確率を出力する関数とします。
今回は、GeneratorとDiscriminatorがそれぞれパラメータ\(\theta_{g}\), \(\theta_{d}\)によって特徴づけられているとします。
GANが構成する生成モデル
GANの生成モデルを定義するため、潜在空間\(\mathcal{Z}\)上の確率分布\(p_{z}(z)\)を定義します。
確率分布\(p_{z}(\mathbf{z})\)は、サンプリングが容易な確率分布ならば特に問題はありません(一様分布やガウス分布等に設定することが多いです)
この分布を用いて、GANの生成モデルは以下のように定義されます。
定義: GANの生成モデル
$$p(\mathbf{x}; \theta_{g}) \equiv \int d\mathbf{z} p_{z}(\mathbf{z}) \delta \left( \mathbf{x} – G(\mathbf{z};\theta_{g}) \right) $$
ここで、\(\theta_{g}\)は生成モデルのパラメータを表す。また、\(\delta(x)\)はデルタ関数を表す。
すなわち以下の関係を満たす。
$$\int f(x) \delta(x) dx = f(0)$$
すなわち、サンプリングが容易な潜在変数をある決定的な関数\(G\)によって変換して得られる確率分布です。
このような分布は、決定的な関数によって押し出された分布であることから、push-foward分布と呼ばれます。
そして、GANの目的は、\(p(\mathbf{x}; \theta_{g})\)を用いて、データの背後にある確率分布\(q(\mathbf{x})\)を近似することです。
仮に、データの生成過程を支配する確率分布\(q(\mathbf{x})\)を高精度で表現できたとしたら、GANは、Generatorにより本物のデータと統計的に類似した偽物データ生成できることになります。
GANの構造と役割
これで下準備は整いました。
ここからは、GANの基本となる構造をもう一度整理します。
GANの基本的な構造と役割
下の図と対応させて各々の役割を整理してください。
- 学習データ(本物データ)\(\mathbf{x}_{\text{data}}\) : Discriminatorへの入力となり、偽物のデータと比較検討され本物・偽物かが判断される。
- 乱数ベクトル \(\mathbf{z}\) : Generatorへの入力となり、偽物データ\(\mathbf{x}_{\text{fake}}\)に変換される。
- Generator : 乱数ベクトル\(\mathbf{z}\)をもとに偽物データ\(\mathbf{x}_{\text{fake}}\)を生成する。
- Discriminator : 本物データ\(\mathbf{x}_{\text{data}}\)と偽物データ\(\mathbf{x}_{\text{fake}}\)を入力として、本物である確率を出力する。
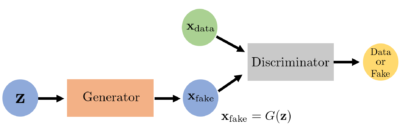 GANのネットワーク
GANのネットワーク
では、GeneratorとDiscriminatorを敵対的に切磋琢磨させながら学習させるためにはどうすれば良いでしょうか??
そのためには、通常の機械学習と同様にGeneratorとDiscriminatorがどの程度目的を達成しているのかを評価する目的関数が必要です。
以降では、GANの目的関数を詳しく説明していきます。
GANの目的関数

ここからは、GANを学習するための目的関数を説明していきます。
GANの目的関数
早速ですが、GANの目的関数は以下のような形になります。
定義 : GANの目的関数
上述で説明したGANの生成機により構成される確率分布\(p\)を用いると以下のように表すことができます。
この目的関数の形に着目すると以下の二つが分かります。
- 目的関数が大きくなる場合、Discriminatorは本物のデータと偽物のデータを正しく識別可能な状態
- 目的関数が小さくなる場合、Discriminatorは本物のデータを偽物と識別して、偽物のデータを本物と識別する状態
この性質から、各モデルに対しては以下のように目的関数を構築すれば良いことが分かります。
定義 : 各モデルの目的関数
- Generatorの目的関数
$$V_{G}(G, D;\theta_{g}, \theta_{d}) \equiv V(G, D;\theta_{g}, \theta_{d})$$
- Discriminatorの目的関数
$$V_{D}(G, D;\theta_{g}, \theta_{d}) \equiv~ – V(G, D;\theta_{g}, \theta_{d})$$
このように構成すれば、各々の目的関数を同時に最小化すれば、切磋琢磨のような学習が実現できそうですね。
しかし、通常の機械学習と異なり各モデルの目的関数が単一のモデルのパラメータのに依存するわけではなく、\(\theta_{d}\), \(\theta_{d}\)の二つのモデルのパラメータに依存します。
さらに、GeneratorとDiscriminatorの目的関数の最適化条件は以下の条件を満たします。
上記の各モデルの目的関数の最適解は以下を満たす。
$$ V(G^{\ast}, D^{\ast}) = \underset{\theta_{g}}{\min} \underset{\theta_{d}}{\max} V(G, D; \theta_{g}, \theta_{d}) $$
この\(\underset{\theta_{g}}{\min} \underset{\theta_{d}}{\max} V(G, D; \theta_{g}, \theta_{d})\)という状態は、ゲーム理論的には、ナッシュ均衡という状態に対応します。
最終的には、GANの学習を\(\underset{\theta_{g}}{\min} \underset{\theta_{d}}{\max} V(G, D; \theta_{g}, \theta_{d}) \)という形まで持っていくことができました。
あとは、この最適化問題を一般的な機械学習と同様に、数値的に解けば良いですね…
しかし、この目的関数のmin-maxの値を得ることで、\(p(\mathbf{x})\)を\(q(\mathbf{x})\)に近づけることは可能なのでしょうか??
実は、理論的にパラメータ\(\theta_{g}, \theta_{d}\)の空間が十分大きければ可能となることが示せます。
以降、この点を詳しく解説していきます。
GANの目的関数のmin-max値

今回は、上述で導出した最適化問題の解が、生成モデルとして相応しいのかを考えていきます。
ここからは、\(p(\mathbf{x}; \theta_{g})\)と\(D(\mathbf{x}; \theta_{d})\)の関数空間が十分広いことを仮定して解析していきます(どんな値も取りうることができると思ってください)
そのことを明示的に表すために\(p(\mathbf{x}; \theta_{g})\)と\(D(\mathbf{x};\theta_{d})\)を\(p(\mathbf{x})\)と\(D(\mathbf{x})\)と表すことにします。
目的関数の最大化
まずは、Discriminatorの最適化(目的関数の最大化)を考えます。
目的関数が以下のように表せることを思い出しましょう。
\begin{align}V(G, D) = &\int d\mathbf{x}\left\{q(\mathbf{x}) \log D(\mathbf{x}) + p(\mathbf{x}) \log \left( 1 – D(\mathbf{x}) \right) \right\}\end{align}
\(D\)の関数からなる空間の中で、上記の目的関数を最大化するような関数を求める問題は、変分問題と呼ばれます。
通常の最適化問題との違いは、パラメータではなく、目的関数を最大とするような関数を探索することです。
変分問題だけでも様々な理論がありますが、今回は詳細に立ち入らず使用する公式を紹介する程度に留めます。
今回の変分問題は、以下のような便利な公式が使用できます。
変分問題の公式
以下のような目的関数を考える。
$$\mathcal{L}[f] = \int L(x, f(x)) dx$$
この目的関数の停留関数(最大化または最小化を実現する関数)\(f(x)\)は以下の方程式を満たす。
$$\frac{dL(x, f(x))}{df(x)} = 0$$
つまり、通常の最大値・最小値を求めるように微分ができる。
汎関数\(V(G, D) \)は\(D\)に関して微分可能なので、上記の公式を使うと\(D\)の停留条件は以下のように計算できます。
この方程式を解くと最適なDiscriminatorは以下の条件を満たすことがわかります。
次に、この条件を代入して、目的関数の最小化を考えていきます。
目的関数の最大化
次に先ほど求めた目的関数を最小化する\(D^{\ast}\)を代入して、目的関数の最大化を実行していきます。
まずは、前節で導出した\(D^{\ast}\)を\(V(G, D) \)に代入し、以下のように変形します。
この\(V(G, D^{\ast})\)を最小化する\(q\)は、最後の式のKLダイバージェンスが両方とも0になれば良いので、以下のような条件が導かれます。
$$q = \frac{q + p}{2} = p$$
ゆえに、\(q = p\)となることが示されました。
これで、目的関数のmin-maxを実行するとデータの確率分布\(q(\mathbf{x})\)がGANの確率分布\(p(\mathbf{x})\)となることが示されました。
実は、最後の式は、確率分布間の距離を表すJensen-Shannonダイバージェンスという形になっています。
つまり、GANの学習は、Jensen-Shannonダイバージェンスを最小化していることになります。
Jensen-Shannonダイバージェンスの解説に関しては、下記が参考になります。
また、min-maxを実行すると\(q=p\)となるため、最適化されたDiscriminatorは、以下のようになります。
\(D^{\ast}(\mathbf{x}) = \frac{1}{2}\)
すなわち、min-max最適化が実行されると、Discriminatorはデータが本物なのか偽物なのかが完全に見分けがつかなくなり、ランダムに識別するようになります。
GANを実装するときの最適化

理論上では、\(V(G, D)\)の期待値を評価する必要がありますが、現実的には評価するのが不可能です。
そのため、実際\(V(G, D)\)を計算するときは、実際にGeneratorから生成された偽物サンプル集合と実際のデータ集合の平均を取ることで近似的に評価します。
実際のライブラリで実装ときは、Binary Cross Entropyによる表現を理解しておくと、様々な教科書の実装例が理解しやすくなります。
ここでは、実装も視野に入れてBinary Cross Entropyを使用する表現も説明します。
Binary Cross Entropyによる表現
Pytorch等でGANを実装する場合、目的関数\(V(G, D; \theta_{g}, \theta_{d})\)をBinary Cross Entropy(BEC)で表現します。
ここからは、BECによる表現方法を説明していきます。
まずは、ご存知の方も多いかもしれませんが、BECを以下のように定義されます。
Binary Cross Entropy
\(t \in \{0, 1\}\), \(f(\mathbf{x}) \in [0, 1]\)に対して、BCEを以下で定義される。
本物サンプルに対して\(t = 1\)を割り当て、偽物のサンプルに対して\(t=0\)を割り当てるようにすると、以下のように\(V(G, D;\theta_{g}, \theta_{d})\)をBCEを使って表現することができます。
- 本物のサンプルに対するBEC
$$L_{\text{BCE}:t = 1} = \underset{\mathbf{x} \sim q}{\mathbb{E}} \left[\log D(\mathbf{x};\theta_{d}) \right] $$
- 偽物のサンプルに対するBEC
$$L_{\text{BCE}: t=0} = \underset{\mathbf{z} \sim p_{z}}{\mathbb{E}} \left[\log \left( 1 – D(G(\mathbf{z}; \theta_{g});\theta_{d}) \right) \right] $$
目的関数の期待値をサンプル平均に置き換える
データの分布関数は一般に未知なので期待値を解析的に評価することは不可能です。
また、\(q(\mathbf{x}; \theta_{g})\)も一般に複雑な形になるので期待値を解析的に評価することはできません。
そのため期待値を以下のようにサンプリング系列の平均で近似します。
サンプリングによる期待値の近似
仮に\(p(\mathbf{x})\)に従うサンプル点\(\{\mathbf{x}^{(i)}\}_{i=1}^{M}\)が得られたとき、期待値を以下で近似する。
$$\mathbb{E}_{\mathbf{x} \sim p(\mathbf{x})} \simeq \frac{1}{M} \sum_{i=1}^{M} \mathbf{x}^{(i)}$$
このサンプリングによる期待値の近似をGANの目的関数に使用します。
具体的には、\(M\)個の\(\{\mathbf{z}^{(i)} \}_{i=1}^{M}\)から生成される\(M\)個の偽物サンプルと\(M\)個のデータ\(\{\mathbf{x}_{(j)} \}_{i=1}^{M} \)を利用し、\(V(G, D; \theta_{d}, \theta_{g})\)を近似的に以下で評価します。
サンプルリング平均によるGANの目的関数の評価
GANの問題点
GANの学習には以下のような問題点があります(代表的な課題のみ紹介します)
- 勾配消失問題
- モード崩壊
- 目的関数の収束性
- 過剰な汎化
- 訓練をいつ止めるべきかが不明
① : 勾配消失
初期段階、すなわちGeneratorがほぼランダムなサンプルを生成して、Discriminatorがほとんど完全に本物か偽物かを識別ができるとき、目的関数の形状から勾配消失が起こってしまいます。
② : モード崩壊
モード崩壊とは、学習データのいくつかのモードが、ほとんど生成されなくなる問題です。
例えば、猫・犬・馬の画像をGANに学習させた場合、猫と犬の画像は生成できますが、馬の画像はほとんど生成できない状況です。
③ : 目的関数の収束性
GANは、ハイパーパラメータの設定によっては、目的関数が収束しないことがあります。
当然、大きなネットワークを使用する場合は、学習が収束するまでに膨大な時間がかかります。
④ : 過剰な汎化
モード崩壊に反して、過剰に汎化しすぎて余計なモードを学習してしまうことも課題の一つです。
先程の例なら、犬・猫・馬の写真があって、猫と馬を融合させたような写真を生成してしまったらまずいですよね…
訓練をいつ止めるべきか不明
損失関数の値と画像のクオリティが必ずしも相関しないため、いつ学習を止めるのかが不明になります。
GANの問題点の解決方法
これまで、説明してきた問題点を回避する方法は大きく分けて以下の三つに分けられます。
- DiscriminatorとGeneratorのモデルを改良
- 目的関数を改良
- 学習手法を改良
③ : 学習手法を改良
GANを学習する際に経験的に良いとされている改良例を紹介します。
学習手法の改良例
- 入力の画素値を1〜 -1の間に正規化
- バッチ正則化
- 勾配制約 (*悪影響を起こす可能性もある)
- 識別の方を多く学習する
- 勾配が疎になるのを防ぐ
- averaging poolingを使用する
- Leaky ReLUを使用する
この工夫をしたからといって必ず上手くいくというものではありません。
そのため、参考程度に認識しておいてください。
GANの評価指標

GANには、生成されるサンプルの良さを明示的に判断する評価指標が存在しません(これまで紹介してきた目的関数は直接的に生成サンプルと学習データを比較しているわけではないことに注意してください)
では、どのように生成されたサンプルの品質を評価したら良いでしょうか?
最初に思いつくのは、学習データを使用して尤度関数を計算することだと思います。
しかし、近似的に尤度関数を評価するためには、計算量や準備のためのコストが大きいです。
また、尤度関数に基づく評価は、他にも多くの問題を含んでいます(先程紹介した過度な汎化などが生じます)
その代わりに使われる評価指標は、主に以下の二つです。
- IS(インセプション・スコア)
- FID(フレチェのインセプション距離)
詳細は述べませんが、この二つを使用することでサンプルの質を評価する問題は、ほとんど解決することができます。
参考資料
下記に参考文献・参考URLを示します。
参考文献
参考文献を説明していきます。
実践GAN 敵対的生成ネットワークによる深層学習
実装のテクニック等も詳しく書いてあります。
ディープラーニングと物理学 原理がわかる、応用ができる
物理的な定式化が最高です。
参考URL
参考URLを解説します。
- Generative Adversarial Nets : 原論文です。普通に読みやすいです。
- An Annotated Proof of Generative Adversarial Networks with Implementation Notes : とてもわかりやすい解説です。他の記事も非常に勉強になります。
まとめ
GANを定式化し、生成モデルとしてどのように学習するべきかを説明しました。
GANは、他の生成モデルのようにKL ダイバージェンス最小化で定式化されていないところが特徴です。
本記事には、誤植や理解の勘違いが含まれている可能性があります。
もし間違いを見つけた場合は、筆者のTwitter(努力のガリレオのTwitterはこちら)や記事のコメント欄にそっとコメントしてください…
本記事が皆様の役に立つことを願います…

『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。
















