【入門】グラフィカルモデルと統計的機械学習

本記事では、グラフィカルモデルの概要と統計的機械学習の枠組みを紹介します。

本記事を読むことでグラフィカルモデルを使ってデータの背後に仮定される確率分布を近似的に再現する学習モデルを学習する方法を学ぶことができます。

本記事の結果を利用することとで、さまざまな学習モデルの学習方程式を導出することができます。

【入門】生成モデルと統計的機械学習について機械学習の一つである生成モデルの基本的な枠組みについて説明しました。これらの枠組みを最初の段階で理解することで高度なモデルも理解することが可能になります。...

グラフィカルモデルについて
グラフィカルモデルと統計的機械学習
- グラフィカルモデルを学習モデルに設定
- 無向グラフィカルモデルの隠れユニット
無向グラフィカルモデル（エネルギーベースモデル）の統計的機械学習
- 可視変数のみのモデル
- 隠れ変数をもつモデル
参考文献
まとめ

グラフィカルモデルについて

数学のグラフの定義からグラフィカルモデルの導入とメリットを順番に説明していきます。

グラフについて
グラフィカルモデルについて
グラフィカルモデルのメリット

グラフについて

ここで考えるグラフは皆さんがイメージしているようなグラフではなくて、数学的なグラフです。

数学的なグラフとは、ノード（頂点 or 頂点）集合$\Omega = \{\Omega_{1}, \ldots, \Omega_{N} \}$と、そのノードを結合したエッジ（リンク）集合$\mathcal{E} = \{E_{ij} \mid V_{i}, V_{j} \text{の間にエッジが存在} \} $の構造物を表します。

すなわち、数学的なグラフは、$(\Omega, \mathcal{E})$によって定義されます。

エッジの中でも、方向をもち矢印で書かれるもの（有向エッジ）と、方向を持たないもの（無向エッジ）の２種類があります。

一般的には、$ \Omega_{i} $, $\Omega_{j}$の有向エッジは$\Omega_{i} \to \Omega_{j} $と表され、無向エッジは$\Omega_{i} – \Omega_{j}$と表されます。

全てのエッジが方向を持つグラフを『有効グラフ』と呼び、方向を持たないものを『無向グラフ』と呼びます。

典型的な例を下に示します。

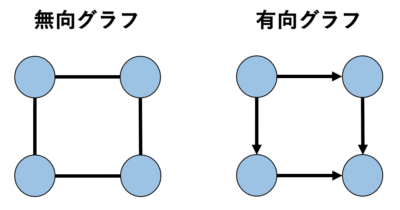
グラフ理論では、すべてのノード対がエッジで結ばれているグラフを『完全グラフ』といいます。

グラフィカルモデル

ある確率変数をグラフの各ノードに、その確率変数間の関係性（条件付き独立性）をエッジに対応させたグラフを『グラフィカルモデル』といいます。

有効グラフに確率変数を対応させたものを、『有効グラフィカルモデル（ベイジアンネットワーク）』といい、『無向グラフィカルモデル（マルコフ確率場）』といいます。

実はマルコフ確率場となるためにはもう少し条件が必要ですが、本記事を読む際は同じものだと思っても問題はありません。

一応、形式的に定義すると以下のようになります。

マルコフ確率場

無向グラフ$(\Omega, \mathcal{E})$上の確率分布$P(\mathbf{X})$に対して、各確率変数$\mathbf{X} = \{X_{i} \mid i \in \Omega \}$に対して以下が成り立つとき確率分布$P(\mathbf{X}$をマルコフ確率場という。

$$\forall i \in \Omega,~~P(\mathbf{X}) =P(X_{i}\mid \mathbf{X}_{\partial_{i}})P(\mathbf{X}_{\backslash \mathcal{N}_{i}}\mid \mathbf{X}_{\partial_{i}})$$

ここで、$\partial i$はノード$\Omega_{i}$の最近接ノード集合表し、$\mathcal{N}_{i}$は、ノート$\Omega_{i}$と$\partial i$の和集合を表す。

また、このような性質を『局所マルコフ性』という。

定義は一見難しそうですが、主張していることは簡単で、$\mathbf{X}_{i}$の最近接の確率変数の実現値が与えられた場合、$\mathbf{X}_{i}$と最近接以外の全ての確率変数と独立になるということです。

グラフィカルモデルをメリット

グラフィカルモデルの最大のメリットは、ノードに対応させた確率変数間の条件付き独立性を表現することができ、同時確率分布をコンパクトな条件付き確率の積で因数分解可能なことです！

また、視覚的に確率変数間の関係を捉えることができるため近似アルゴリズム開発の開発にも役に立ちます。

『条件付き独立性がよくわからん…』という方は下記を参考にしてください。

条件付き独立性

独立ではない確率変数が、他の変数で条件つけることで独立になる性質のことです。

つまり、条件付き独立な確率変数は、以下のように通常では独立になりませんが、

$$P(A, B) \neq P(A)P(B)$$

他の変数で条件つけることで、独立になる確率変数です。

$$P(A, B \mid C) = P(A \mid C) P(B \mid C)$$

無向グラフィカルモデル（マルコフ確率場）

今回は、無向グラフィカルモデルのケースを考えるため詳しい解説はしませんが、有効グラフィカルモデルの場合は、矢印が条件付き確率による因果関係に直接対応します。

では、無向グラフィカルモデルの場合はどうなるでしょうか？

一般に無向グラフィカルモデルでは、無向グラフの構造に従ってエネルギー関数$E(\mathbf{x})$を定義します。

ここで、$\mathbf{x} = (x_{1}, x_{2}, \ldots, x_{N})^{\text{T}}$を表します。

このようなエネルギー関数を用いて、以下のような確率モデルを無向グラフに対応させます。

$$ P(\mathbf{x}) = \frac{1}{Z} \exp \left(- E(\mathbf{x}) \right)$$

ここで、$Z$は分配関数と呼ばれ、全ての可能な$ \mathbf{x} $に関する確率の総和$\sum_{\mathbf{x}} P(\mathbf{x}) = 1$にするための規格化定数を表し、以下のように定義されます。

$$Z = \sum_{\mathbf{x}} \exp \left(- E(\mathbf{x}) \right) = \sum_{x_{1}} \sum_{x_{2}} \cdots \sum_{x_{N}} \exp \left(- E(\mathbf{x}) \right) $$

よく使用されるエネルギー関数としては以下のような形があります。

$$E(\mathbf{x}) = ~- \sum_{i \in \Omega} \phi_{i}(x_{i}) ~- \sum_{\{i, j\} \in \mathcal{E}} \psi_{ij}(x_{i}, x_{j})$$

各項は以下のように呼ばれます。

$ \phi_{i} $ : バイアス項と呼ばれ、各ノードの取る値の偏りを表す
$ \psi_{ij} $ : 重み（結合項）と呼ばれ、確率変数間の関係性を表す

これらの具体的な関数系は、与えられたタスクに応じて自分でカスタマイズします。

グラフィカルモデルと統計的機械学習

グラフィカルモデルと統計的機械学習の関係について説明していきます。

統計的機械学習という言葉を初めて聞いた方は下記を一読してみてください。

グラフィカルモデルを学習モデルに設定

統計的機械学習とは、与えられたデータから生成モデルを構築することを意味します。

具体的には、学習モデルを仮定し、その学習モデル特徴づけるパラメータをデータから決定することで構築します。

しかし、『学習モデルを仮定する』と一言で言われても難しいですよね。

適切に学習モデルを仮定する際には、「事前知識をどのように学習モデルに埋め込むべきか？」というのが重要になりそうです。

そこで、事前に与えられている因果関係や、変数同士の関係性をうまく可視化できるグラフィカルモデルが役に立つのです。

無向グラフィカルモデルの隠れユニット

これまでのモデルでは、与えられたデータと確率変数が一対一対応するように学習モデル（グラフィカルモデル）を構成していました。

しかし、実際の観測データでは情報が欠損していることも多いです…

そこで、一つの対処策としてはデータに対応しない確率変数をグラフィカルモデルに加えて冗長なネットワークを構築するという手法が考えられます。

そのような、データに対応しない確率変数を『隠れ変数』と呼びます。

本記事では、グラフのノードに対応していた変数$\mathbf{x}$をデータに対応する変数（可視変数）$ \mathbf{v} = (v_{1}, v_{2}, \ldots v_{N_{v}})^{\text{T}} $と表し、隠れ変数を$ \mathbf{h} = (h_{1}, h_{2}, \ldots h_{N_{h}})^{\text{T}} $と表すことにします。

ここで、可視変数の総数を$N_{v}$とし、隠れ変数の総数を$N_{h}$としました。

無向グラフィカルモデル（エネルギーベースモデル）の統計的機械学習

今回は、無向モデル（エネルギーベースモデル）の統計的機械学習に焦点を当てて解説していきます。

ここで、与えられたデータから学習モデルのパラメータを決定する方法として、『KLダイバージェンス最小化』という手法を利用します。

以下では、学習モデルのパラメータをまとめて$\theta$と書くことにします。

＊データの経験分布と学習モデルのKLダイバージェンス最小化は、最尤推定によるパラメータ推定と一致するため最尤推定をしていると思っても良いです。

可視変数のみのモデル

可視変数のみのモデルの場合は、エネルギー関数$E(\mathbf{x} ; \theta) $によって学習モデルは以下のように定義されます。

$$P(\mathbf{x} \mid \theta) = \frac{1}{Z} \exp \left(- E(\mathbf{x} ; \theta) \right),~~~~~ Z = \sum_{\mathbf{x}} \exp \left(- E(\mathbf{x} ; \theta) \right)$$

この学習モデルと経験分布の間のKL Divergenceを最小化するようにパラメータを選びます。

$$\text{D}_{\text{KL}}(\theta) = \sum_{\mathbf{x}} \hat{Q}(\mathbf{x}) \log \frac{\hat{Q}(\mathbf{x})}{P(\mathbf{x} \mid \theta)} $$

最小値を求めるために微分する値を見つけます。

\begin{align}\frac{\partial}{\partial \theta} \text{D}_{\text{KL}}(\theta) &= \frac{\partial}{\partial \theta} \sum_{\mathbf{x}} \hat{Q}(\mathbf{x}) \left(\log \hat{Q}(\mathbf{x}) – \log P(\mathbf{x} \mid \theta) \right) \\ &= ~ – \frac{\partial}{\partial \theta} \sum_{\mathbf{x}} \hat{Q}(\mathbf{x}) \log P(\mathbf{x} \mid \theta) \\ &= 0 \end{align}

ここで、仮定した学習モデルを代入することでさらに計算を進めることができます。

\begin{align} – \frac{\partial}{\partial \theta} \sum_{\mathbf{x}} \hat{Q}(\mathbf{x}) \log P(\mathbf{x} \mid \theta) &= \frac{\partial}{\partial \theta} \sum_{\mathbf{x}} \hat{Q}(\mathbf{x}) \left(\log e^{-E(\mathbf{x} ; \theta)} – \log Z \right) \\ &= \sum_{\mathbf{x}} \hat{Q}(\mathbf{x}) \left(\frac{\partial E}{\partial \theta} \right) – \sum_{\mathbf{x}} P(\mathbf{x} \mid \theta) \left(\frac{\partial E}{\partial \theta} \right) \\ &= \left\langle \frac{\partial E}{\partial \theta} \right\rangle_{\text{data}} – \left\langle \frac{\partial E}{\partial \theta} \right\rangle_{\text{model}} \end{align}

ここで、$ \langle \cdots \rangle_{data} = \sum_{\mathbf{x}} \hat{Q}(\mathbf{x}) \cdots $を表し、$ \langle \cdots \rangle_{model} = \sum_{\mathbf{x}} P(\mathbf{x} \mid \theta) \cdots $を表します。

このような連立方程式を学習方程式と呼ぶこともあります。

一般に、この連立方程式を解くことは難しいため、以下のようなアルゴリズム（勾配降下法）を用いて数値的に解きます。

$$\theta^{(t+1)} \leftarrow \theta^{(t)} ~- \epsilon \left(\left\langle \frac{\partial E}{\partial \theta} \right\rangle_{\text{data}} – \left\langle \frac{\partial E}{\partial \theta} \right\rangle_{\text{model}} \right) $$

隠れ変数をもつモデル

まず、隠れ変数と可視変数をもつエネルギー$ E({\bf v}, {\bf h} ; \theta) $を用いて以下のような確率分布を定義する。

$$P({\bf v}, {\bf h} \mid \theta) = \frac{1}{Z} e^{- E({\bf v}, {\bf h} ; \theta)} ,~~~~~ Z = \sum_{{\bf v}, {\bf h}} e^{- E({\bf v}, {\bf h} ; \theta)} $$

隠れ変数をもつモデルは、以下のように隠れ変数を周辺化したモデルを学習モデルに採用します。

$$P(\mathbf{x} \mid \theta)({\bf v}) = \sum_{{\bf h}}P({\bf v}, {\bf h} \mid \theta) $$

同様に、この学習モデルと経験分布の間のKL Divergenceが最小になるようにパラメータを決定します。

\begin{align}\frac{\partial}{\partial \theta} \text{D}_{\text{KL}}(\theta) &= ~ – \frac{\partial}{\partial \theta} \sum_{\mathbf{x}} \hat{Q}(\mathbf{x}) \log P(\mathbf{x} \mid \theta) \\ &=~ – \frac{\partial}{\partial \theta} \sum_{{\bf v}} \hat{Q}({\bf v}) \left(\sum_{\bf h} e^{- E({\bf v}, {\bf h} ; \theta)} – \log Z \right) \\ &= \sum_{{\bf v}} \hat{Q}({\bf v}) \sum_{{\bf h}} P({\bf h} \mid {\bf v}) \left(\frac{\partial E}{\partial \theta} \right) – \sum_{{\bf v}, {\bf h}} P({\bf v}, {\bf h}) \left(\frac{\partial E}{\partial \theta} \right) \\ &= \left\langle \frac{\partial E}{\partial \theta} \right\rangle_{data} – \left\langle \frac{\partial E}{\partial \theta} \right\rangle_{model} \end{align}

ここで、$ \langle \cdots \rangle_{data} = \sum_{\mathbf{x}} \hat{Q}(\mathbf{x}) \sum_{{\bf h}} P({\bf h} \mid {\bf v}) \cdots $を表し、$ \langle \cdots \rangle_{model} = \sum_{\mathbf{x}} P(\mathbf{x} \mid \theta) \cdots $を表します。

同様に、以下のようなアルゴリズム（勾配降下法）を用いて数値的に解きます。

$$\theta^{(t+1)} \leftarrow \theta^{(t)} ~- \epsilon \left(\left\langle \frac{\partial E}{\partial \theta} \right\rangle_{data} – \left\langle \frac{\partial E}{\partial \theta} \right\rangle_{model} \right)$$

これで、隠れ変数をもつタイプのモデルも学習できます。

参考文献

参考文献について紹介します。

パターン認識と機械学習下

リンク

確率的グラフィカルモデル

リンク

深層学習 Deep Learning

リンク

これならわかる深層学習入門

リンク

深層学習

リンク

どの本もわかりやすくオススメです。

まとめ

グラフィカルモデルと統計的機械学習について簡単に説明しました。

グラフィカルモデルについて
グラフィカルモデルと統計的機械学習
無向グラフィカルモデルの統計的機械学習

これらの一般論を理解しておくことで、ボルツマンマシンや制限ボルツマンマシンの学習法を簡単に理解することができます。

また、上記の考え方は一般のグラフィカルモデルに対して成り立つため新たなモデルを作成するときのベースラインになります。

また、筆者の誤植や理解の違いがあった場合は、Twitter等でコメントいただけると幸いです。

【大学生・大学院生限定】Amazon Prime Studentが圧倒的におすすめ

『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。

Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…

主な理由は以下の通りです。

『Amazon Prime』のサービスを年会費半額で利用可能
本が最大10%割引
文房具が最大20%割引
日用品が最大15%割引
お急ぎ便・お届け日時指定便が使い放題
6ヶ月間無料で使用可能

特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです！

少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。

専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww

より詳しい内容と登録方法については下記を参考にしてください。

Prime Studentの特典・登録方法【学生限定最強特典！】Prime Studentの特典・登録方法【学生限定最強特典！】学生にとって超おすすめな『Prime Student』のメリット...

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。

【入門】グラフィカルモデルと統計的機械学習（マルコフ確率場）