【入門】相対性理論とは(ローレンツ変換)
実は、相対性理論は決してスピリチャルな理論ではなく『認めなくてはいけない二つの原理』から様々な直感と反する事実が生じる理論です。
この記事では、大学1年生からでも理解できるように相対性理論の初歩から説明していきます。
記事を読み終えると、今まで勉強してきたニュートン力学がある種の近似理論であることに気づきます。
*(iphone・Androidの方へ)数式はスクロール可能です。
相対性理論入門:認めなくてはいけない二つの原理

相対性理論を考える時に認めなくてはいけない二つの原理があります。
認めなくてはいけない二つの原理
- 光速度不変の法則
- 特殊相対性原理
いきなり驚きましたよね。
安心してください、詳しく説明していきます。
① 光速度不変の法則
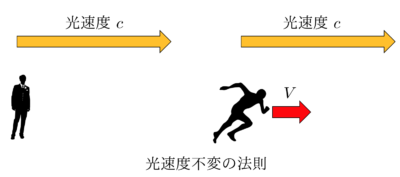
光速度不変の原理というのは文字通り、どんな立場から観測しても光の速度が変化しないという原理です。
つまり、上の図のように止まっている人から光を観測しても、速度\(v\)で走ってる人から光を観測しても光の速度は変わらないということです。
これは、かなり不思議な現象ですよね。例えば、高速道路で同じ速度で走っている車は止まって見えますよね?
光の場合は、例え光速度程度で走っている車があったとしても光は速度が変わらず、時速30万キロで進みます。
*多くの有名な実験で妥当性は評価されています。
② 相対性原理
相対性原理とは、『どの慣性系から見ても物理法則が成り立つ』という原理です。
具体的には、物理法則を記述する電磁気学のマックスウェル方程式や力学の運動方程式はどの慣性系でも不変に成り立つという原理です。
慣性系とは、静止している人から見た座標系と等速直線運動をしている人から見た座標系と認識しておけばOKです。
相対性理論入門:ガリレイ変換の問題点とローレンツ変換

ガリレイ変換とは、別の慣性系への変換を以下のような式で考えることです。
$$ r^{\prime} = r – v t $$
この変換では、加速度は変化しないので別の慣性系でも以下のように運動方程式は成立する。
$$ m a^{\prime} = F $$
しかし、大きな問題が起きてしまいます…
この変換則では、別の慣性系のマックスウェル方程式が大きく変わってしまいます。
つまり、特殊相対性原理を満たすためには新たな変換則を考える必要が出てきてしまいます。
「ガリレイ変換でも、日常生活では計算結果に問題は起きないではないか」と思う方もいるかもしれませんが、日常生活では、あらゆる速度が光速よりはるかに遅いため、光速が無限に速いという近似が成り立ち計算結果がよく合います。後ろの方で詳しく説明するので安心してください
新しい変換則の導入
ガリレイ変換では、特殊相対性原理が成り立たなくなってしまいます。
なので、以下の三つの性質を満たすような新たな座標変換を考えましょう。
- 特殊相対性原理
- 光速度不変の原理
- 光速が無限に見える近似の元でガリレイ変換と等価な変換になっている
新しい座標変換を考えるための問題設定
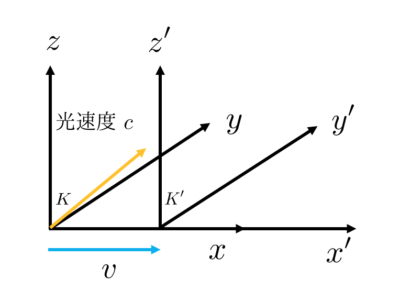
三つの性質を満たすための座標変換を考えていきます。
まず、静止系\(K(x, y, z, t)\)と\(x\)軸方向へ速度\(v\)で運動している系\(K^{\prime}(x^{\prime},y^{\prime},z^{\prime}) \)を考えます。
仮定として、\(t = 0\)で二つの座標系の原点が一致していることにして、\(K(x,y,z,t)\)の静止座標系の原点から、\(t = 0 \)で光を放つことにします。
新しい変換(ローレンツ変換)を導出する①
先ほどの問題設定で、\(K(x,y,z,t)\)の静止座標系の原点から、\(t = 0 \)で光を放つと\(t\)秒後には、原点から\(ct\)だけ離れた球面状に分布します。
数式でかくと以下のように書くことができます。
$$ x^{2} + y^{2} + z^{2} = (c t )^{2} $$
さらに、光速度不変の法則から等速\(v\)で動いている座標系からも同じように観測されます。
ゆえに以下のように定式化できます。
$$ (x^{\prime})^{2} + (y^{\prime})^{2} + (z^{\prime})^{2} = (c t )^{2} $$
この条件のもと、\(K\)の座標系から\(K^{\prime}\)の座標系への変換規則を求めることを考えます。
具体的には、以下の変換式を考えます。
$$ \left( \begin{array}{c} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ t^{\prime} \end{array} \right) = \left( \begin{array}{cccc} a_{1} & a_{2} & a_{3} & a_{4} \\ a_{5} & a_{6} & a_{7} & a_{8} \\ a_{9} & a_{10} & a_{11} & a_{12} \\ a_{13} & a_{14} & a_{15} & a_{16}\end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ t \end{array} \right) $$
\(x^{2} \)などの項が入っていない理由は、条件式に代入するとその係数が恒等的に0になってしまうからです。
新しい変換(ローレンツ変換)を導出する②
本来ならば、16個の変数の連立方程式を計算して\( a_{1} \) 〜 \(a_{16}\)を求める必要がありますが、計算方法は、一般的な教科書に載っていてそこまで難しくないので答えのみ紹介します。
$$ x^{\prime} = \frac{x ~- vt}{\sqrt{1 ~- \frac{v^{2}}{c^{2}}}} $$
$$ t^{\prime} = \frac{ ~- vx / c^{2} + t}{ \sqrt{1 ~- \frac{v^{2}}{c^{2}}}} $$
$$ y^{\prime} = y ~~~,~~~z^{\prime} = z $$
このような変換則を『ローレンツ変換』と言います
ローレンツ変換とガリレイ変換
この変換が以下の三つの性質を満たすことを思い出してみましょう。
- 特殊相対性原理
- 光速度不変の原理
- 光速が無限に見える近似の元でガリレイ変換と等価な変換になっている
①と②に関しては、ローレンツ変換が満たしていることがわかります(マックスウェル方程式をローレンツ変換してみると良いです)
なので、③の仮定である『光速が無限に見える近似のもとでガリレイ変換と等価な変換になっている』という性質を確かめていきましょう。
確かめる方法は簡単です。
以下の式の\( ( c \rightarrow \infty ) \)を考えれば良いのです。
$$ x^{\prime} = \frac{x ~- vt}{\sqrt{1 ~- \frac{v^{2}}{c^{2}}}} ~~,~~ t^{\prime} = \frac{ ~- vx / c^{2} + t}{ \sqrt{1 ~- \frac{v^{2}}{c^{2}}}} $$
するとこの式は以下のようにかけます。
$$ x^{\prime} = x ~- v t ~~,~~ t^{\prime} = t $$
確かにガリレイ変換になっていますね。
逆に光速度程度で動く物体の場合は、計算結果が一致しなくなってしまうということですね。具体的に光速程度で動く物質は、実は身近にある電子などが該当します。
ローレンツ変換の対称性
得られた変換則を少し変形してみます。
どのように変形するかというと、以下のように文字(ものさし)を置き換えるだけです
$$ \omega = c t ~~,~~\beta = \frac{v}{c} ~~,~~ \gamma = \frac{1}{\sqrt{1 – \frac{v^{2}}{c^{2}}}} $$
すると変換則は以下のように書くことができます。
$$ x^{\prime} = \gamma ( x ~- \beta \omega ) ~~,~~ \omega = \gamma ( – \beta x + \omega ) $$
こうみるとかなり対称性の良い形になっていますね。
ローレンツ変換の不変量
通常の回転変換では原点からの距離が不変に保たれます。
$$ r^{2} = x^{2} + y^{2} + z^{2} = (x^{\prime})^{2} + (y^{\prime})^{2} + (z^{\prime})^{2} $$
では、ローレンツ変換の不変量はどうなるのでしょうか。
実は以下のような不変量が存在します。
このような性質を持つ空間を『ミンコフスキー空間』と言います。
参考資料
参考サイト
参考文献
まとめ(相対性理論入門)

まず、相対性理論を考える上で認めなくてはならない二つの原理を説明しました。
認めなくてはいけない二つの原理
- 光速度不変の法則
- 特殊相対性原理
その後、通常のガリレイ変換では相対性原理を満たさない物理法則(マックスウェル方程式)が存在してしまうため、新たな変換則を導出しました。
その変換則を『ローレンツ変換』といいます。
実は、このローレンス変換から様々な直感と反する現象が生じてきます。
次回は、あの有名な\( E = m c^{2} \)を導出することに挑戦しましょう。

『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。