【今度こそわかる】開集合と閉集合をわかりやすく解説しました
閉集合と開集合の理解は、大学数学を学ぶ上で必要不可欠なものです。
本記事では、数学的な厳密を少し避けながら、開集合と閉集合をわかりやすく解説します。
開集合・閉集合を理解するための基礎(集合族、添え字)

ここでは、高校の集合の範囲を少し超えたレベルの説明します。
- 集合族
- 添え字
これらは集合論の教科書には、あたり前のように書かれるので理解しておくと良いです。
集合論の基本① 集合族
集合族とは、いくつかの集合をつけて並べたもののことです。
具体的には、集合\(A_{1}, A_{2}, A_{3}, \cdots, A_{n} \)を、以下のように並べたものが集合族です。
$$ \{ A_{1}, A_{2}, A_{3}, \cdots, A_{n} \} $$
少し言い方がしつこいですが、『集合の集合』です。
集合論の基本② 添え字
より一般的に集合族を特徴づけるために添字集合というものを使用することが多いです。
具体的には、何かある集合\( \Lambda \)の各元\( \lambda \)を、一つずつ集合\(A_{\lambda} \)を対応させ、その元によって特徴づけられる集合族\( \{A_{\lambda}\}_{\lambda \in Lambda} \)を考えます(下記にイメージを示します)
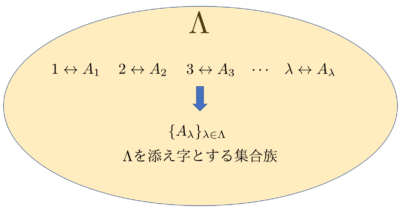
この時\(\lambda\)を\(A_{\lambda}\)の添え字といい、\( \{A_{\lambda}\}_{\lambda \in \Lambda} \)を\( \Lambda \)を添え字集合とする集合族といいます。
開集合と閉集合を理解しよう
開集合と閉集合を理解するために基礎知識を説明した後、開集合と閉集合を図を用いながら解説していきます。
開集合と閉集合を理解しよう
- ε近傍
- 極限点
- 開集合
- 閉集合
ε近傍
点\(a \in \mathbb{R}^{m} \)の\( \epsilon \)近傍( \( N_{\epsilon}( a; \mathbb{R}^{m}) \) )とは\( a \)からの距離が\(\epsilon\)未満であるような点の全体の集合です。
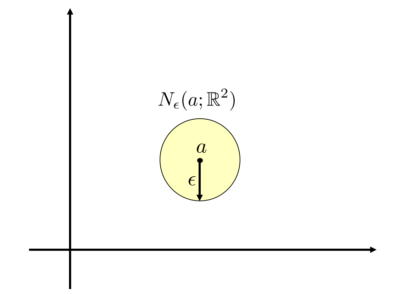
具体的には以下のように書くことができます。
$$ N_{\epsilon}(a;\mathbb{R}^{m}) = \{ x \in \mathbb{R}^{m} | d(x,a) < \epsilon \} $$
極限点
\( \mathbb{R}^{m} \)の点列\( \{ x_{n} \}_{n = 1}^{\infty} \)が\(a\)のε近傍をどんなに小さくしても大きな\( n_{k} \)を選べば、それ以降の点列が全て\( N_{\epsilon}(a;\mathbb{R}^{m} ) \)に属する時、点列\( \{ x_{n} \}_{n = 1}^{\infty} \)は点\(a\)に収束するといい以下のように書きます。
$$ \lim_{n \to \infty} x_{n} = a $$
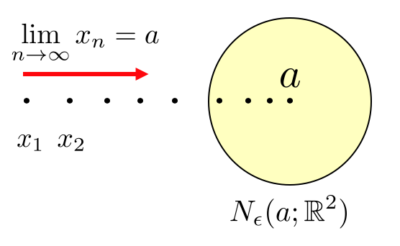
図は、ある\(x_{n}\)以降からε近傍に属するイメージを表しています。
開集合
\( \mathbb{R}^{m} \)の部分集合\(U\)が開集合の時、\(U\)の中の任意の点\(a\)が、\( \epsilon > 0 \)を十分小さくすると以下の関係が成り立ちます。
$$ N_{\epsilon}(a;\mathbb{R}^{m}) \subset U $$
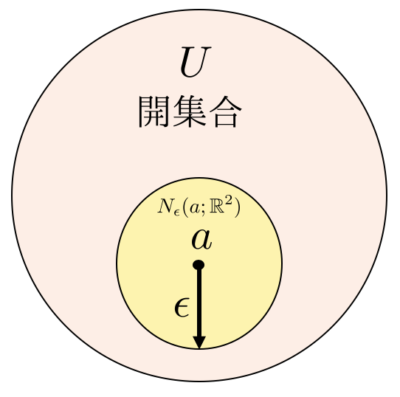
つまり、開集合\(U\)の中の任意の点では必ずε近傍が定義できるというということです。
*空集合\(\emptyset\)は開集合であることを約束することが多いです。
閉集合
集合\(C\)の任意の点列\( \{ x_{n} \}_{n = 1}^{\infty} \)が\(x \in \mathbb{R}^{m} \)に収束すれば、点\(x\)は\(C\)に属することを\(C\)が閉集合であるといいます。
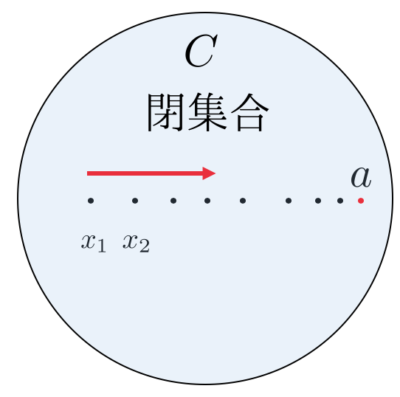
集合\(C\)の全ての点で成り立つ必要があるので、境界部分の点も含める必要があります。
開集合と閉集合の関係
開集合と閉集合には以下のような二つの関係が成り立ちます。
- \(U\)が\( \mathbb{R}^{m} \)の開集合なら、補集合\( \mathbb{R}^{m} – U \)は\( \mathbb{R^{m}}\)の閉集合
- \(C\)が\( \mathbb{R}^{m} \)の閉集合なら、補集合\( \mathbb{R}^{m} – C \)は\( \mathbb{R^{m}}\)の開集合
細かい証明は行いませんが、知っておくと良い命題です。
参考資料
参考文献
まとめ
集合論の基礎をまとめました。
開集合や閉集合は大学数学を学ぶ際に必要不可欠な知識です。
いろいろなところに応用されている多様体を学ぶためにも、今回学んだ知識は定着させておきましょう。

『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。