【Python】制限ボルツマンマシン（RBM）の実装と理論｜PyTorchによるGPU化

本記事では、制限ボルツマンマシン（RBM）の理論とPythonによる実装を初学者の方でも理解できるように解説します。

Pythonによる実装では、RBMの実装でよく使用される手法であるパーシステント・コンストラスティブ・ダイバージェンス法（PCD法）と呼ばれる手法を使用して実装しました。

後半部分では、PythonによるRBMの具体的なコードを載せているので、適当に動かして遊んでみてください。

制限ボルツマンマシン（RBM）の定義と学習法
制限ボルツマンマシンの近似的学習法
制限ボルツマンマシンの誤差関数
- 擬似対数尤度（Pseudo-likelihood）
PytorchによるRBMの実装
参考資料
- 参考文献
- 参考論文
まとめ

制限ボルツマンマシン（RBM）の定義と学習法

まずは、制限ボルツマンマシンの定義と学習法を説明していきます。

制限ボルツマンマシンの定義
制限ボルツマンマシンの学習法
制限ボルツマンマシンの学習方程式の導出

制限ボルツマンマシン（RBM）の定義

制限ボルツマンマシン（Restricted Boltzmann Machine ; RBM）の目的は、「データの生成過程を支配する確率分布（経験分布）」を模倣することです。

例えば、サイコロからサイコロの目を観測すると、おそらく（5, 3, 2, 6, 1, 1, …）のように1〜6の目が等確率で生成されます。まさに、それがデータを支配する確率分布そのものです。サイコロの場合は、イメージがしやすいですが、一般のデータにもサイコロのようなデータの生成過程を支配する確率分布が背後に存在することを仮定します。

その目的のために制限ボルツマンマシンは、パラメータ$\theta = (\mathbf{w} \in \mathbb{R}^{N_{v} \times N_{h}}, \mathbf{b} \in \mathbb{R}^{N_{v}}, \mathbf{c} \in \mathbb{R}^{N_{h}} )$を持つ次の確率分布を導入します。

$$P(\mathbf{v}, \mathbf{h} ; \theta) = \frac{1}{Z(\theta)} e^{- E(\mathbf{v}, \mathbf{h} ; \theta)} $$

ここで、関数$E(\mathbf{v}, \mathbf{h} ; \theta)$は一般にエネルギー関数と呼ばれ、RBMの場合以下のように定義されます。

$$E(\mathbf{v}, \mathbf{h} ; \theta) =~ – \sum_{i=1}^{N_{v}} \sum_{j=1}^{N_{h}} w_{ij} v_{i} h_{j} ~- \sum_{i=1}^{N_{v}} b_{i} v_{i} ~- \sum_{j=1}^{N_{h}} c_{j} h_{j}$$

具体的にネットワークの結合をグラフィカルモデルで可視化したものを以下に示します。

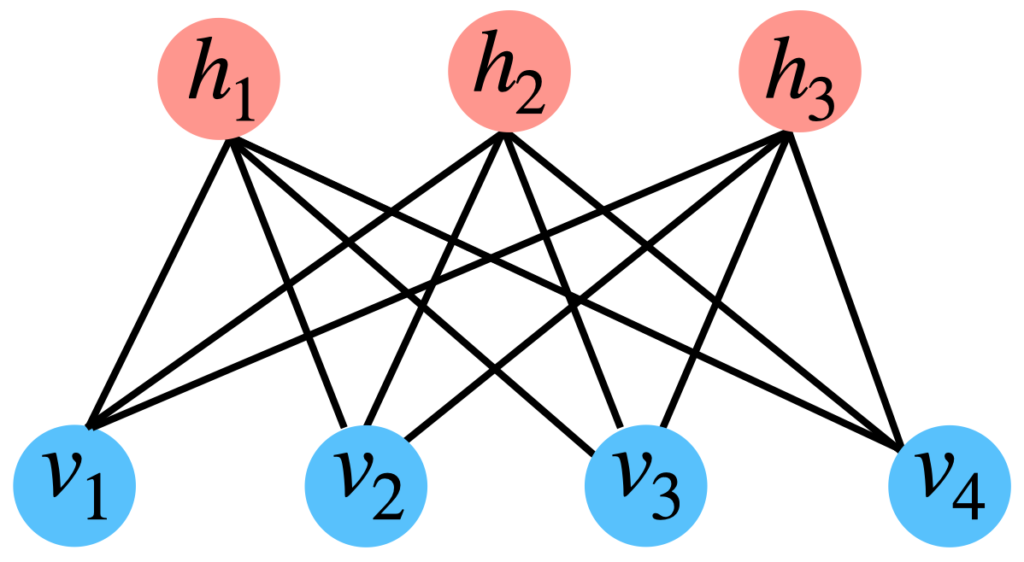制限ボルツマンマシンの具体例

一般に変数$v_{i}$, $h_{j}$はそれぞれ可視変数、隠れ変数と呼ばれ$v_{i} \in \{0, 1\}$, $h_{j} \in \{0, 1\}$の値をとります。

また、$Z(\theta)$は一般に分配関数と呼ばれ以下のように定義されます。

$$Z(\theta) = \sum_{\mathbf{v}, \mathbf{h}} e^{- E(\mathbf{v}, \mathbf{h} ; \theta)} $$

ここで、$\sum_{\mathbf{v}, \mathbf{h}} \cdots $は可視変数と隠れ変数に関して可能な状態全てに関する和を取ることを意味しています。

そして、制限ボルツマンマシンは、隠れ変数に関して周辺化した次の確率分布を学習モデルとしてデータの背後にある確率分布を近似的に表現します。

\begin{align} P(\mathbf{v} ; \theta) &= \sum_{\mathbf{h}} P(\mathbf{v}, \mathbf{h} ; \theta) \\ &= \frac{1}{Z(\theta)} e^{\sum_{i} b_{i} v_{i}} \prod_{j} \sum_{h_{j}} e^{(\sum_{i} w_{ij} v_{i} + c_{j})h_{j}} \\ &= \frac{1}{Z(\theta)} e^{\sum_{i} b_{i} v_{i}} \prod_{j} \left(1 + e^{(\sum_{i} w_{ij} v_{i} + c_{j})} \right) \\ &= \frac{1}{Z(\theta)} e^{\sum_{i} b_{i} v_{i} + \sum_{j} \log \left( 1 + e^{(\sum_{i} w_{ij} v_{i} + c_{j})} \right) } \end{align}

隠れ変数があって一見わかりにくいですが、隠れ変数に関して周辺化したモデルを見ると、次のエネルギー関数を持つ確率モデル$p(\mathbf{v} ; \theta)$を用いて、データの生成過程を模倣しようとしているだけです。

$$E(\mathbf{v}; \theta) =~ – \sum_{i} b_{i} v_{i}~ – \sum_{j} \log \left( 1 + e^{(\sum_{i} w_{ij} v_{i} + c_{j})} \right)$$

一見、隠れ変数があるときは、２次形式の単純なエネルギー関数$E(\mathbf{v}, \mathbf{h};\theta)$見えましたが、実際は、$E(\mathbf{v}; \theta)$のような非線形で複雑な確率モデルによるモデリングになっています。

RBMの条件付き独立性

RBMの最大のメリットは、ネットワーク構造に由来する「条件付き独立性」と呼ばれる性質です。ここでは、その条件付き独立性を詳しく説明していきます。

例えば、可視変数に関する条件付き確率を計算すると次のように表せます。

$$P(\mathbf{v} \mid \mathbf{h}; \theta) = \prod_{i} \frac{e^{(b_{i} + \sum_{j} w_{ij} h_{j})v_{i}}}{1 + e^{(b_{i} + \sum_{j} w_{ij} h_{j})}} $$

これは、一方の層を固定したときに他方の層の変数が因数分解の形（独立）で表せることを意味しています。まさに、この性質が「条件付き独立性」です。

同様に、隠れ変数に関しても同様の関係式を得ることができます。

$$P(\mathbf{h} \mid \mathbf{v}, \theta) = \prod_{j} \frac{e^{(c_{j} + \sum_{i} w_{ij} v_{i})h_{j}}}{1 + e^{(c_{j} + \sum_{i} w_{ij} v_{i})}} $$

RBMの学習方程式

データ$\mathcal{D} = \{\mathbf{v}^{1},\ldots, \mathbf{v}^{P}\}$が与えられたときに、RBMのパラメータ$\theta$の学習は、一般に以下の対数尤度最大化によってパラメータを決定します。

$$\mathcal{L}_{\mathcal{D}}(\theta) \equiv \frac{1}{P} \sum_{\mu=1}^{P} \ln p(\mathbf{v}^{\mu} \mid \theta)$$

上式を最大化するようなパラメータを見つけるためにパラメータに関して微分して$0$となる条件を求めると以下のような条件式を導くことができます。

$$\mathbb{E}_{\text{data}} \left[ \frac{\partial E(\mathbf{v}^{\mu}, \mathbf{h} ; \theta)}{\partial \theta} \right] = \mathbb{E}_{\text{RBM}} \left[ \frac{\partial E(\mathbf{v}^{\mu}, \mathbf{h} ; \theta)}{\partial \theta} \right]$$

ここで、$\mathbb{E}_{\text{data}}[\cdots]$は以下のような平均操作を表します。

$$\mathbb{E}_{\text{data}}[\cdots] = \frac{1}{P} \sum_{\mu} \sum_{\mathbf{h}} p(\mathbf{h} \mid \mathbf{v}^{\mu}, \theta) \cdots$$

また、$\mathbb{E}_{\text{RBM}}[\cdots]$は以下のような平均操作を表します。

$$\mathbb{E}_{\text{RBM}}[\cdots] = \sum_{\mathbf{v}, \mathbf{h}} p(\mathbf{v}, \mathbf{h} \mid \theta) \cdots$$

実際に各パラメータに関して計算すると以下のような連立方程式を得ることができます。

\begin{align}&\frac{\partial \mathcal{L}_{\mathcal{D}}(\theta)}{\partial w_{ij}} : \mathbb{E}_{\text{data}}[v_{i} h_{j}] = \mathbb{E}_{\text{RBM}}[v_{i} h_{j}] \\ &\frac{\partial \mathcal{L}_{\mathcal{D}}(\theta)}{\partial b_{i}} : \mathbb{E}_{\text{data}}[v_{i}] = \mathbb{E}_{\text{RBM}}[v_{i}] \\ &\frac{\partial \mathcal{L}_{\mathcal{D}}(\theta)}{\partial c_{j}} : \mathbb{E}_{\text{data}}[h_{j}] = \mathbb{E}_{\text{RBM}}[ h_{j}]\end{align}

この連立方程式を一般に『RBMの学習方程式』と呼びます。

RBMの学習法

RBMの学習方程式を得られましたが、一般に学習方程式（超特大の連立方程式…）を解析的に解くのは困難なため、数値的に以下の勾配上昇法によってパラメータを逐次更新し学習を実行します。

RBMの学習更新式（勾配上昇法）

\begin{align}&w_{ij}^{(t+1)} \leftarrow w_{ij}^{(t)} + \eta \big( \mathbb{E}_{\text{data}}[v_{i} h_{j}] – \mathbb{E}_{\text{RBM}}[v_{i} h_{j}] \big) \\ &b_{i}^{(t+1)} \leftarrow b_{i}^{(t)} + \eta \big(\mathbb{E}_{\text{data}}[v_{i}] – \mathbb{E}_{\text{RBM}}[v_{i}] \big) \\ &c_{j}^{(t+1)} \leftarrow c_{j}^{(t)} + \eta \big( \mathbb{E}_{\text{data}}[h_{j}] – \mathbb{E}_{\text{RBM}}[ h_{j}] \big) \end{align}

ここで、$\eta \in \mathbb{R}$は一般に学習率と呼ばれ小さな値をとります。

この更新式を収束するまで更新し続けます。

また、RBMではデータに関する平均の項を『ポジティブフェーズ（positive phase）』と呼び、RBMの確率分布に関する項を『ネガティブフェーズ（negative phase）』と呼びます。

ここまでの結果をまとめると学習方程式を解析的に解く問題が、各更新でネガティブフェーズとポジティブフェーズを評価する問題になりました。

EMアルゴリズムのように対数尤度の最大化を目指しても良いです。

EMアルゴリズムの場合は、次のようにE-stepとM-stepを繰り返してください。

E-step : 現在のパラメータ$\theta^{t}$を用いて次のQ関数$Q(\theta; \theta^{t}) $を計算

$$Q(\theta; \theta^{t}) = \mathbb{E}_{\mathrm{data}}\left[\sum_{\mathbf{h}} P(\mathbf{h} \mid \mathbf{v}; \theta^{t}) \log P(\mathbf{v}, \mathbf{h} ; \theta) \right]$$

M-step : Q関数を最大にする$\theta^{t+1}$でパラメータを更新

EMアルゴリズムの場合も、M-stepの最大化でネガティブフェーズを含むため本質的にはあまり変わらないことに注意してください。

＊EMアルゴリズムがよくわからないという方は特に気にせず読み進めていただいても問題はありません。

ポジティブフェーズとネガティブフェーズの評価は簡単？

ここまでくると、パラメータを学習する問題は、各更新でネガティブフェーズとポジティブフェーズを評価する問題に変わりました。

では、ネガティブフェイズとポジティブフェーズの評価は簡単でしょうか？？

以下では、この疑問を丁寧に答えていきます。

ポジティブフェイズ（positive phase）の評価

positive phaseは以下の期待値を評価することに相当することを思い出しましょう。

$$\mathbb{E}_{\text{data}}[\cdots] = \frac{1}{P} \sum_{\mu} \sum_{\mathbf{h}} p(\mathbf{h} \mid \mathbf{v}^{\mu}, \theta) \cdots$$

まず、データに関する標本平均は簡単に取ることができます。

また、隠れ変数に関する条件付き確率に関する平均もRBMの条件付き独立性のため簡単に評価することができます。

あまりにデータ数が多い場合は、mini-batch法などを使用すれば基本的に問題はありません。

ネガティブフェイズ（negative phase）の評価

negative phaseは以下の期待値を評価することを思い出しましょう。

$$\mathbb{E}_{\text{RBM}}[\cdots] = \sum_{\mathbf{v}, \mathbf{h}} p(\mathbf{v}, \mathbf{h} \mid \theta) \cdots$$

つまり、$p(\mathbf{v}, \mathbf{h} \mid \theta)$の計算を行う必要があります。

しかし、$p(\mathbf{v}, \mathbf{h} \mid \theta)$を評価するためには以下の分配関数を評価する必要があります。

$$Z = \sum_{\mathbf{v}, \mathbf{h}} e^{- E(\mathbf{v}, \mathbf{h} ; \theta)} $$

繰り返しになりますが、$\sum_{\mathbf{v}, \mathbf{h}} \cdots$は$\mathbf{v}$, $\mathbf{h}$の可能な状態に関する和を取ることを意味しています。

仮に可視変数と隠れ変数が$20$個あったら、状態数は約$1.0 \times 10^{6}$となってしまいます。

このような状態和の計算は一般に困難で『計算量爆発』と呼ばれたりします。

そのため、Negative Phaseに関しては近似的学習法により評価することで学習を行います。

次章では、Negative Phaseの近似的学習法に関して説明していきます。

制限ボルツマンマシンの近似的学習法

これまで、制限ボルツマンマシンの学習は、ネガティブフェイズ（negative phase）の計算が計算量爆発になり困難であることを説明しました。

ここからは、ネガティブフェイズ（negative phase）の計算を近似的に行う手法を紹介していきます。

＊ネガティブフェイズ（negative phase）の効率的かつ精度の高い評価方法は現在も進行中の研究のため、現時点で最も一般的な近似計算方法を紹介していきます。

マルコフ連鎖モンテカルロ法による期待値の近似評価
ギブスサンプリングによる評価と問題点
コンストラスティブダイバージェンス法（CD法）
パーシステントコンストラスティブダイバージェンス法（PCD法）

マルコフ連鎖モンテカルロ法による期待値評価

作戦としては、ネガティブフェイズ（negative phase）の期待値評価を$P(\mathbf{v}, \mathbf{h}; \theta)$から具体的にサンプルを生成して、そのサンプルの平均により次のように評価します。

$$\mathbb{E}_{\mathrm{RBM}}[f(\mathbf{v}, \mathbf{h})] = \frac{1}{P} \sum_{\mu=1}^{P} f(\mathbf{v}^{\mu}, \mathbf{h}^{\mu})$$

ここで、$(\mathbf{v}^{\mu}, \mathbf{h}^{\mu})$は、$P(\mathbf{v}, \mathbf{h}; \theta)$から生成されたサンプルです。当然、サンプル数$P$が多ければ多いほど期待値は高精度に近似することができます。

しかし、ここで問題になるのは、$P(\mathbf{v}, \mathbf{h}; \theta)$から実際にサンプルを得る方法です。

確率分布からサンプルを取得する方法は、複数知られていますが、RBMでは高次元の確率分布からサンプルを取得するのに有効な「マルコフ連鎖モンテカルロ法」と呼ばれる方法を使用します。

しかし、詳細や裏側の理論は省略し、以降ではアルゴリズムとして$P(\mathbf{v}, \mathbf{h}; \theta)$を取得する方法を説明していきます。

＊マルコフ連鎖モンテカルロ法の詳細を知ってから学びたいという方は、下記を一読してから戻ってきてください。

モンテカルロ法の基本をわかりやすく説明してみた｜マルコフ連鎖モンテカルロ法（MCMC）まで本記事では、初心者でも理解できるようにモンテカルロ法の基本的な概念からマルコフ連鎖モンテカルロ法までを段階的に説明しました。さらに、適宜Pythonによるシミュレーションを行いながら視覚的に理解できるように努めました。...

ギブスサンプリングによる評価と問題点

制限ボルツマンマシンは、マルコフ連鎖モンテカルロ法の中でもギブスサンプリングという手法を利用することが多いです。

具体的には、以下のようなアルゴリズムで$P(\mathbf{v}, \mathbf{h} \mid \theta)$からのサンプル列を取得します。

制限ボルツマンマシンのギブスサンプリング

$\mathbf{v}$をランダムに初期化し、$\mathbf{v}^{0}$と定義する
$P(\mathbf{h} \mid \mathbf{v}^{0}) $から、$\mathbf{h}^{0}$をサンプルする
$P(\mathbf{v} \mid \mathbf{h}^{1}) $から、$\mathbf{v}^{1}$をサンプルする
①〜②を繰り返す

＊条件付き独立の性質から各サンプルの要素$v_{i}^{t}$を一つ一つサンプルするのではなく、並列的に全ての要素$\mathbf{v}^{t}$をサンプルすることができます（$\mathbf{h}^{t}$も同様）

イメージ的には、以下のようになります。

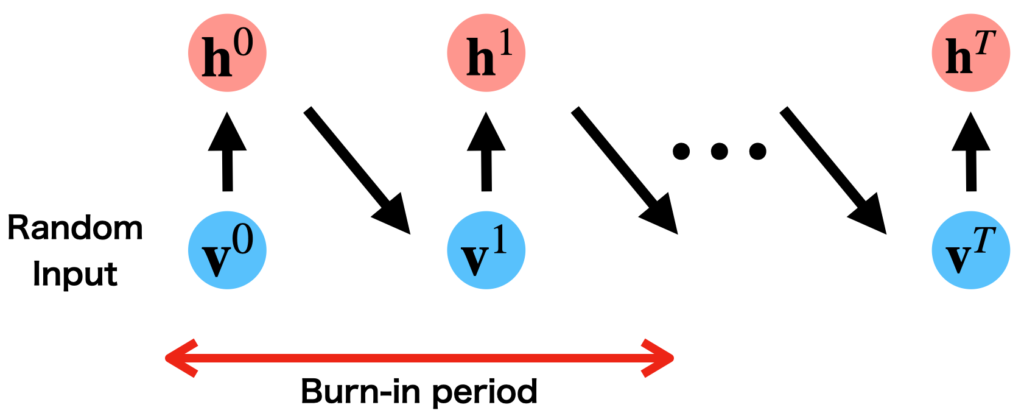ギブスサンプリングのイメージ

ここで、マルコフ連鎖の性質から、最初の段階は定常分布$P(\mathbf{v}, \mathbf{h} \mid \theta)$からサンプルとはみなせず、定常状態になっていない初期のサンプルは標本平均を計算するためのサンプル列から外します。

そして、定常状態に到達するまでのおおよその時間を『バーンイン（burn-in）』と言います。

また、一つのサンプル$\mathbf{v}^{0}$をサンプルした後に、$\mathbf{v}^{1}$を標本平均を計算するためのサンプル列の候補として選ぶのもNGです。

理由は、直後のサンプル$\mathbf{v}^{1}$は$\mathbf{v}^{0}$と統計的に相関しているからです。

そのため、サンプルを一つ得たら、十分間隔を開けて新たなサンプルをサンプル列に加える必要があります。

それを避けるための方法として、ランダムな多数の初期値から独立に走らせた複数のマルコフ連鎖から、独立に一つずつサンプルを採用する方法を使用することができます。

しかし、計算コストは減ったものの勾配更新のたびにギブスサンプリングを実行することは、依然として計算コストは高く、実用的なレベルとは言えません。

そのためさらに大胆な近似手法であるコンストラスティブ・ダイバージェンス法（Constrastive Divergence ; CD法）を使用します。

ギブスサンプリングを実際に動かしてみたいという方は下記を下記を一読してください。

【Python】ギブスサンプリングの応用（多変量ガウス分布）本記事では、ギブスサンプリンの理解を深めるためにガウス分布への適用例を紹介します。アルゴリズムの詳しい説明とPythonによる実装を紹介しています。...

コンストラスティブ・ダイバージェンス法（Constrastive Divergence ; CD法）

コンストラスティブ・ダイバージェンス法（Constrastive Divergence ; CD法）では、ネガティブファイズの評価を以下の$k$回の連鎖から得られるサンプルの値で近似するという考え方です。

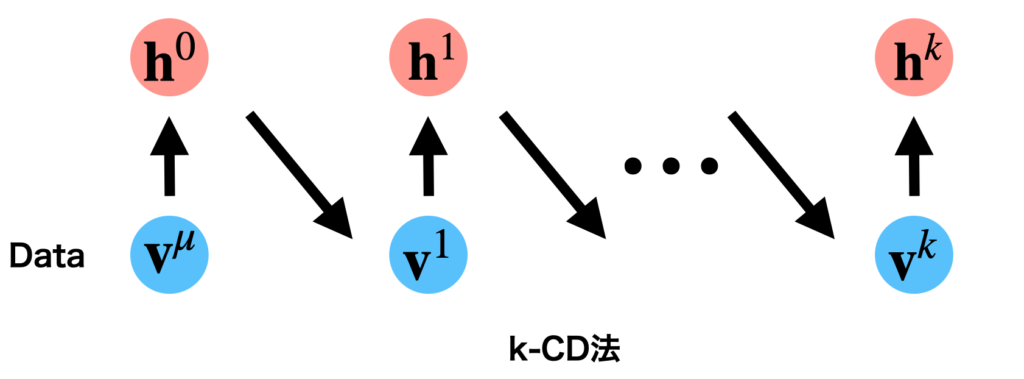k-CD法のイメージ

具体的な勾配更新式は以下のようになります。

k-CD法による勾配更新①

\begin{align}&w_{ij}^{(t+1)} \leftarrow w_{ij}^{(t)} + \eta \big( \mathbb{E}_{\text{data}}[v_{i} h_{j}] – \mathbb{E}_{P_{k}}[v_{i} h_{j}] \big) \\ &b_{i}^{(t+1)} \leftarrow b_{i}^{(t)} + \eta \big(\mathbb{E}_{\text{data}}[v_{i}] – \mathbb{E}_{P_{k}}[v_{i}] \big) \\ &c_{j}^{(t+1)} \leftarrow c_{j}^{(t)} + \eta \big( \mathbb{E}_{\text{data}}[h_{j}] – \mathbb{E}_{P_{k}}[ h_{j}] \big) \end{align}

ここで、$P_{k}$は$k$回の連鎖から得られたサンプル列による平均を意味します。

具体的には、以下を意味します。

$$\mathbb{E}_{P_{k}}[\cdots] = \frac{1}{k} \sum_{t=1}^{K} \cdots $$

一般的に、k回の連鎖から得られるサンプルを利用するCD法をk-CD法と言います。

また、CD法で勾配を計算する際は、隠れ変数のサンプル値$\mathbf{h}^{t}$を使用するのではなく、条件付き確率$P(\mathbf{h} \mid \mathbf{v}^{t}, \theta)$を使用するのが良いと言われています。

さらに、得られたサンプル列の標本平均ではなく、一つのサンプル$\mathbf{v}^{k}$を使用してネガティブフェイズを評価します。

気持ちとしては、勾配上昇法で更新を繰り返すうちに多数のサンプルの効果が間接的に取り込めるという所に起因しています。

ここまでをまとめると、実用的なk-CD法による勾配上昇式は以下のようになります。

k-CD法による勾配更新②

\begin{align}&w_{ij}^{(t+1)} \leftarrow w_{ij}^{(t)} + \eta \big( v_{i}^{\mu} P(h_{j}=1 \mid \mathbf{v}^{\mu}, \theta)~ – v_{i}^{k} P(h_{j}=1 \mid \mathbf{v}^{k}, \theta) \big) \\ &b_{i}^{(t+1)} \leftarrow b_{i}^{(t)} + + \eta \big( v_{i}^{\mu} – v_{i}^{k} \big) \\ &c_{j}^{(t+1)} \leftarrow c_{j}^{(t)} + \eta \big(P(h_{j}=1 \mid \mathbf{v}^{\mu}, \theta)~ – P(h_{j}=1 \mid \mathbf{v}^{k}, \theta) \big) \end{align}

パラメータを更新した後は、訓練サンプルから新たなサンプル$\mathbf{v}$を選び更新を繰り返します。

ミニバッチ勾配上昇法を利用する場合は、ミニバッチに含まれるデータを初期値とした複数のマルコフ連鎖を構成し、得られたサンプルの標本平均をとり勾配更新を行います。

なんとk-CD法は1-CD法（連鎖を一回）でも十分な機能を持ち実用的なことが経験的に知られています。

このk-CD法は、勾配更新のたびに$k$回の連鎖を走らせるだけなので、ギブスサンプリングに比べて計算量を大幅に減少できます。

パーシステント・コンストラスティブ・ダイバージェンス法（PCD法）

パーシステント・コンストラスティブダイバージェンス法（Persistent Constrastive Divergence）法は、CD法が定常状態からのサンプリングができないという問題を部分的に解決した方法でCD法以上の効率・精度を経験的に確保することができると言われています。

具体的には以下のような更新を行います。

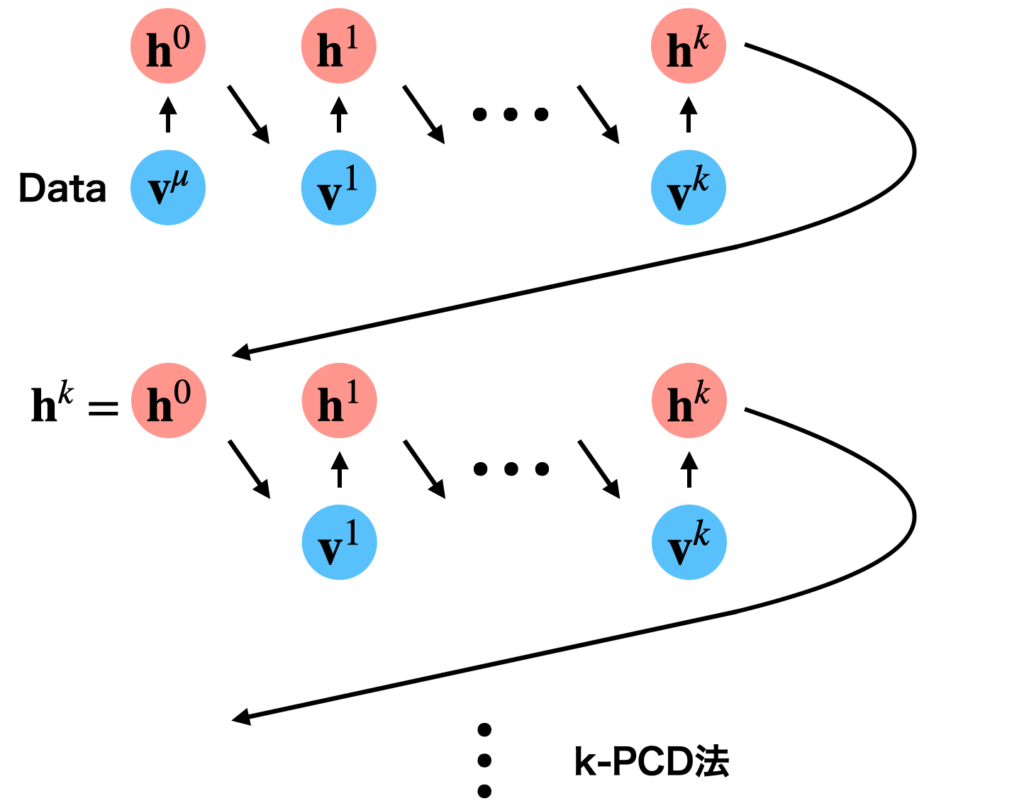k-PCD法のイメージ

k-PCD法では前のパラメータ更新で使用したサンプルを初期値として利用し、再び勾配更新を行う方法です。

現在、RBMを実装する際はPCD法が使用されることが多いです。

制限ボルツマンマシンの誤差関数

制限ボルツマンマシンの学習が順調に進んでいるかどうかを確認するためには、対数尤度または、尤度をチェックする必要があります。

しかし、対数尤度・尤度を計算するためには、分配関数を計算する必要があります…

そのため、直接計算することは計算量困難です。

そこで、近似的に対数尤度を評価する方法が開発されています。

擬似対数尤度（Pseudo-likelihood）

擬似対数尤度は、全ての可視ユニットが独立であると仮定して計算した対数尤度で、対数尤度近似する手法です。

具体的には、以下のように近似します。

疑似対数尤度

$$\text{PLL}({\bf v}) \equiv \log \prod_{i=1}^{m} p(v_{i} | {\bf v}_{-i}) = \sum_{i=1}^{m} \log p(v_{i} | {\bf v}_{-i})$$

ここで、$ {\bf v}_{-i} $は、$v_{i}$以外のユニットの集合です。

この擬似対数尤度は、訓練データ数が大きければ、漸近的に対数尤度に一致することが示されます。

制限ボルツマンマシンの場合、$p(v_{i}|{\bf v}_{-i})$は、以下のように表せます。

制限ボルツマンマシンの疑似対数尤度

$$p(v_{i} | {\bf v}_{-i} ) = \sigma \big(F(v_{i}=0, {\bf v}_{-i}) ~ – F(v_{i}=1, {\bf v}_{-i}) \big) $$

これでも計算量を大幅に減らすことができますが、入力データの次元が大きい時は依然として計算は大変です。

そのため、擬似対数尤度（PLL）を確率的に近似したものがよく使用されます。

$$\hat{\text{PLL}}({\bf v}) = D \cdot \log \sigma \big(F(\hat{{\bf v}}_{\tau} – F({\bf v}) \big) $$

$ \tau $は、各データの要素に関する一様分布を持つ確率変数
$\hat{{\bf v}}_{\tau} $は、$\tau$で指定されるユニットを反転したもの
(e.g. 0 → 1, 1 → 0）

Note :

$$\mathbb{E}_{\tau} [\hat{\text{PLL}}({\bf v}) ] = \text{PLL}({\bf v}) $$

こうすることで、計算量を大きく削減することができました。

それ以外の評価指標は、以下が使われます。

Reconstruction error
Annealed Importance Sampling
Validationデータとtrainingデータの間のaverage自由エネルギー差

PytorchによるRBMの実装

RBMの学習では行列計算を多く含むためGPUを簡単に利用できるPytorchがおすすめです。

GPUを利用したPytorchによるRBMの実装例を共有していきます（GPUが手元になくてもCPUでも動きます）

そのため、GPUが簡単に使用できるGoogle Colaboratoryの使用をおすすめします！

下記を参考にインストールしてください。

【10分完了】Google Colaboratoryのインストール法・使い方Google Colabは、GPUを使用できるため、低コストかつ高速で機械学習の実装を行う際に必要不可欠なツールです。本記事では、Google Colabのインストール方法と注意事項を10〜15分程度でまとめました。...

必要なライブラリをインポート

まずは、下記のコードで必要なライブラリをインポートしてください。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from tqdm.notebook import tqdm

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

# MNIST Datasetの取得
from keras.datasets import mnist

# deviceの設定 (cpu or gpu)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

timeはエポックあたりの計算時間を測るためにインポートしました。

また、tqdmはプログレスバーを表示するためにインポートしました。

また、keras.datasetsのmnistは、MNIST（手書き数字）データセットを取得するために使用します。

サンプルデータを読み込む

下記を実行してサンプルデータを読み込んでください。

(X_train, y_train), (X_test, y_test) = mnist.load_data()

今回はX_trainのみを使用するため、X_trainを一次元配列に変換して、値を0と1の離散値に変換します。

X_train = X_train.reshape(60000, 784) # 1次元に変換
X_train = X_train.astype('float32')   # float32型に変換
X_train /= 255                      # 0.0-1.0に変換
X_train = np.where(X_train <= 0.5, 0.0, 1.0) # 0と1に変換
data = torch.from_numpy(X_train.astype(np.float32)).clone() # tensorに変換

次に、X_trainをpytorchのTensorにへ

ここで、画像を表示する関数を定義して、実際に画像を表示してみましょう。

# 複数の画像を表示する関数
def check_images(x):
    images = np.rollaxis(np.rollaxis(x[0:100].reshape(20, -1, 28, 28), 0, 2), 1, 3).reshape(-1, 20 *28)
    plt.figure(figsize=(10,20))
    plt.imshow(images, cmap='gray')
    plt.grid(False)
    plt.axis('off')
    plt.show()

# 画像を一枚表示する関数
def check_one_image(x):
    image = x[0].reshape(28, 28)
    plt.figure(figsize=(10,20))
    plt.imshow(image, cmap='gray')
    plt.grid(False)
    plt.axis('off')
    plt.show()

実際に確認してみます。

check_images(X_train)

データをPyTorch専用のDatasetを変換するコード

ここからは、PyTorchでRBMを実装するために、PyTorch専用のTensorという配列に変換して、Datasetを作成します。

class MyDataset(torch.utils.data.Dataset):
    def __init__(self, samples):
        self.samples = samples
        
    def __len__(self):
        return len(self.samples)

    def __getitem__(self, idx):
        sample = self.samples[idx]
        return sample

Datasetは、データを一つのデータベースのような形でまとめるPytorch専用のクラスです。

より詳しく知りたい方は下記を参考にしてください。

RBMの実装

Pytorchを使用したRBMのコードは具体例は以下のようになります。

class RBM(nn.Module):
    def __init__(self, vis_dim, hid_dim, initial_std=0.01, device='cpu'):
        super(RBM, self).__init__()
        self.device = device
        self.b = torch.zeros(1, vis_dim,  device=device)
        self.c = torch.zeros(1, hid_dim,  device=device)
        self.w = torch.empty((hid_dim, vis_dim), device=device).normal_(mean=0, std=initial_std)
        
    def _visible_to_hidden(self, v):
        """可視ユニットから隠れユニットをサンプル
        """
        p = torch.sigmoid(F.linear(v, self.w, self.c))
        return p.bernoulli()

    def _hidden_to_visible(self, h):
        """隠れユニットから可視ユニットをサンプル
        """
        p = torch.sigmoid(F.linear(h, self.w.t(), self.b))
        return p.bernoulli()
    
    def _visible_to_ph(self, v):
        """P(h=1|v)を計算
        """
        return torch.sigmoid(F.linear(v, self.w, self.c))

    def sample(self, v, gib_num=1):
        """データをサンプリング
        """
        v = v.view(-1, self.w.size(1)).to(self.device)
        h = self._visible_to_hidden(v)
        for _ in range(gib_num):
            v_gibb = self._hidden_to_visible(h)
            h = self._visible_to_hidden(v_gibb)
        return v_gibb

    def sample_ph(self, v, gib_num=15):
        """phをサンプリング
        """
        v = v.view(-1, self.w.size(1)).to(self.device)
        ph = self._visible_to_ph(v) 
        h = ph.bernoulli()
        # Gibbs Sampling 1 ~ k
        for _ in range(gib_num):
            v_gibb = self._hidden_to_visible(h)
            ph_gibb = self._visible_to_ph(v_gibb)
            h = ph_gibb.bernoulli()
        return ph_gibb

    def energy(self, v):
        """エネルギーを計算
        """
        v_term = torch.matmul(v, self.b.t())
        w_x_h = torch.matmul(v, self.w.t())+self.c
        h_term = torch.sum(F.softplus(w_x_h), dim=1)
        return -h_term-v_term

    def pseudo_likelihood(self, v):
        """疑似対数尤度を計算
        """
        flip = torch.randint(0, v.size(1), (1,))
        v_fliped = v.clone()
        v_fliped[:, flip] = 1-v_fliped[:, flip]
        energy = self.energy(v)
        energy_fliped = self.energy(v_fliped)
        return  v.size(1)*F.softplus(energy_fliped - energy)

    def _update(self, v_pos, lr=0.1):
        """ミニバッチあたりの学習更新
        """
        # positive part
        ph_pos = self._visible_to_ph(v_pos)
        # negative part
        v_neg = self._hidden_to_visible(self.h_states) 
        ph_neg = self._visible_to_ph(v_neg)

        lr = lr/v_pos.size(0)
        # Update W
        update = torch.matmul(ph_pos.t(), v_pos) - torch.matmul(ph_neg.t(), v_neg)
        self.w += lr*update
        self.b += lr*torch.sum(v_pos - v_neg, dim=0)
        self.c += lr*torch.sum(ph_pos - ph_neg, dim=0)
        
        # PCDのために隠れユニットの値を保持
        self.h_states = ph_neg.bernoulli()

    def fit(self, data, n_epoch=10, lr=1e-1, batch_size=128):

        train = MyDataset(data[:int(len(data)*0.7)])
        test = MyDataset(data[int(len(data)*0.7):])
        train_loader = torch.utils.data.DataLoader(dataset=train, batch_size=batch_size, shuffle=True, num_workers=0)
        test_loader = torch.utils.data.DataLoader(dataset=train, batch_size=batch_size, shuffle=True, num_workers=0)
        
        train_loss_avg, val_loss_avg = [], []

        # pcd memory
        self.h_states = torch.zeros(batch_size, self.w.size(0), device=device)
        
        for epoch in tqdm(range(n_epoch)):
            
            train_loss_avg.append(0)
            val_loss_avg.append(0)

            self.train()
            for i, data in enumerate(train_loader):
                data = data.to(self.device)
                self._update(data)
                train_loss_avg[-1] += - self.pseudo_likelihood(data).mean().item()
            train_loss_avg[-1] /= data.size(1)

            self.eval()
            with torch.no_grad():
                for i, data in enumerate(test_loader):
                    data = data.view(-1, self.w.size(1)).to(self.device)
                    val_loss_avg[-1] += - self.pseudo_likelihood(data).mean().item()
                val_loss_avg[-1] /= data.size(1)

            print(f"[EPOCH]: {epoch+1}, [LOSS]: {train_loss_avg[-1]:.4f}, [VAL]: {val_loss_avg[-1]:.4f}")
        return train_loss_avg, val_loss_avg

次は、ここで定義したクラスを使ってMNISTデータセットの学習を実行していきます。

MNISTを使用した数値実験

すでにMNISTデータセットは準備できているので、sklearnのように以下を実行すると学習が実行されます！

# RBMインスタンスの作成
model = RBM(28*28, 256, device=device)
# 学習の実行
train_loss, test_loss = model.fit(data, n_epoch=100, lr=1e-1, batch_size=100)

[EPOCH]: 1, [LOSS]: -1946.8083, [VAL]: -2175.9491
[EPOCH]: 2, [LOSS]: -2300.3520, [VAL]: -2301.9908
[EPOCH]: 3, [LOSS]: -2367.6407, [VAL]: -2466.6865
[EPOCH]: 4, [LOSS]: -2483.8336, [VAL]: -2523.9067
[EPOCH]: 5, [LOSS]: -2538.9095, [VAL]: -2715.3491
[EPOCH]: 6, [LOSS]: -2562.1427, [VAL]: -2594.0387
[EPOCH]: 7, [LOSS]: -2766.7965, [VAL]: -2700.4362
[EPOCH]: 8, [LOSS]: -2789.4425, [VAL]: -2731.5312
[EPOCH]: 9, [LOSS]: -2749.9166, [VAL]: -2694.6613
[EPOCH]: 10, [LOSS]: -2823.9816, [VAL]: -2704.1976
                       :
                       :
                       :

＊学習率やエポック数は適当に選んでいます。各自で変えて挙動がどう変化するか遊んでください。

学習が成功しているのかを確かめるために負の擬似対数尤度を確認してみます。

fig, ax = plt.subplots()
ax.plot(train_loss, marker="o", label="train")
ax.plot(test_loss, marker="o", label="test")
ax.set_xlabel('Epoch', fontsize=30)
ax.set_ylabel(r'$- \hat{\mathrm{PLL}}/N$', fontsize=30)
ax.legend(fontsize=20)
ax.grid()
plt.show()

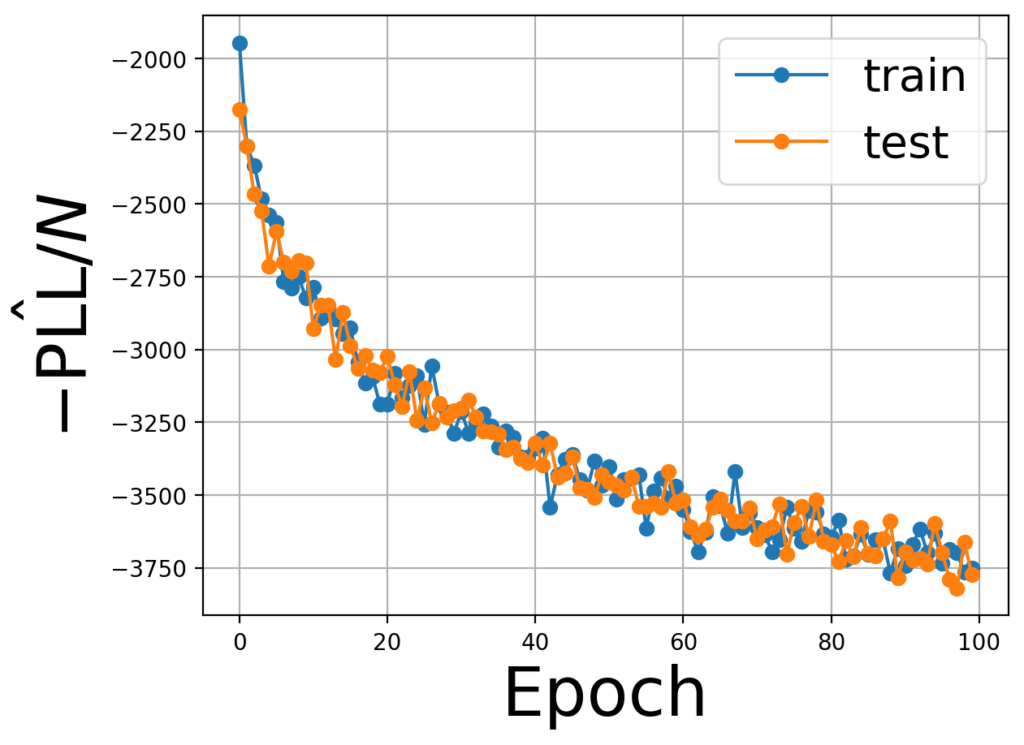
まだ、減少途中のようですが、着実に減少していることがわかります。

最後にRBMによって生成されるデータを実際に確認してみましょう。

学習後のRBMからサンプルを得るためには下記を実行してください。

init_state = data[:100].to(device)
# データを生成
sample = model.sample(init_state, gib_num=200)
# 生成画像を表示
check_images(sample.detach().cpu().numpy())

手書き数字に類似した文字が生成されているのがわかります（多少ノイズがありますが…）

参考資料

参考資料を紹介していきます。

参考文献

参考文献を紹介します。

ボルツマンマシン (シリーズ情報科学における確率モデル 2)

リンク

制限ボルツマンマシンだけでなく、深層ボルツマンマシンやディープビリーフネット等の応用的なモデルの解説が詳しく載っています。

機械学習スタートアップシリーズ　これならわかる深層学習入門

リンク

制限ボルツマンマシン以外にも深層学習に関する基本的な知識を概観できます。

深層学習 (機械学習プロフェッショナルシリーズ)

リンク

後半部分に制限ボルツマンマシンと深層ボルツマンマシンの解説が載っています。

参考論文

参考にした論文を紹介します。

まとめ

制限ボルツマンマシンの理論とPythonによる実装を説明しました。

筆者が勘違いしている可能性は０ではないので、本文は間違いを含むかもしれません。

もし、間違いや理解の違いを見つけた方は、本記事のコメント欄または、努力のガリレオのTwitterにDMしていただけると助かります。

また、本記事で使用したPythonのライブラリやパッケージの使い方は下記を参考に習得してください！

Python Lab

Python学習を効率化させるサービス

Pythonを学習するのに効率的なサービスを紹介していきます。

まず最初におすすめするのは、Udemyです。

Udemyは、Pythonに特化した授業がたくさんあり、どの授業も良質です。

また、セール中は1500円定義で利用することができ、コスパも最強です。

下記の記事では、実際に私が15個以上の講義を受講して特におすすめだった講義を紹介しています。

他のPythonに特化したオンライン・オフラインスクールも下記の記事でまとめています。

自分の学習スタイルに合わせて最適なものを選びましょう。

また、私がPythonを学ぶ際に使用した本を全て暴露しているので参考にしてください。

【Python】制限ボルツマンマシン（RBM）の実装と理論｜PyTorchによるGPU化

制限ボルツマンマシン（RBM）の定義と学習法

制限ボルツマンマシン（RBM）の定義

RBMの条件付き独立性

RBMの学習方程式

RBMの学習法

ポジティブフェーズとネガティブフェーズの評価は簡単？

ポジティブフェイズ（positive phase）の評価

ネガティブフェイズ（negative phase）の評価

制限ボルツマンマシンの近似的学習法

マルコフ連鎖モンテカルロ法による期待値評価

ギブスサンプリングによる評価と問題点

コンストラスティブ・ダイバージェンス法（Constrastive Divergence ; CD法）

パーシステント・コンストラスティブ・ダイバージェンス法（PCD法）

制限ボルツマンマシンの誤差関数

擬似対数尤度（Pseudo-likelihood）

PytorchによるRBMの実装

必要なライブラリをインポート

サンプルデータを読み込む

データをPyTorch専用のDatasetを変換するコード

RBMの実装

MNISTを使用した数値実験

参考資料

参考文献

ボルツマンマシン (シリーズ情報科学における確率モデル 2)

機械学習スタートアップシリーズ　これならわかる深層学習入門

深層学習 (機械学習プロフェッショナルシリーズ)

参考論文

まとめ

【Python】マルコフ連鎖モンテカルロ法の応用｜二次元イジング模型

モンテカルロ法の基本をわかりやすく説明してみた｜マルコフ連鎖モンテカルロ法（MCMC...

【入門】データ同化・状態空間モデルをわかりやすく説明してみた

【Python】棄却サンプリングの実装と理論

【入門】グラフィカルモデルと統計的機械学習（マルコフ確率場）

【東大院生が厳選】量子力学のおすすめ参考書10選｜レベル別に徹底解説！

【東大院生が厳選】力学・解析力学のおすすめ参考書10選｜レベル別に徹底解説！

【東大院生が厳選】微積分（解析学）のおすすめ参考書10選｜レベル別に徹底解説！

トップページ

【東大院生が厳選】電磁気学のおすすめ参考書10選｜レベル別に徹底解説！

制限ボルツマンマシン（RBM）の定義と学習法

制限ボルツマンマシン（RBM）の定義

RBMの条件付き独立性

RBMの学習方程式

RBMの学習法

ポジティブフェーズとネガティブフェーズの評価は簡単？

ポジティブフェイズ（positive phase）の評価

ネガティブフェイズ（negative phase）の評価

制限ボルツマンマシンの近似的学習法

マルコフ連鎖モンテカルロ法による期待値評価

ギブスサンプリングによる評価と問題点

コンストラスティブ・ダイバージェンス法（Constrastive Divergence ; CD法）

パーシステント・コンストラスティブ・ダイバージェンス法（PCD法）

制限ボルツマンマシンの誤差関数

擬似対数尤度（Pseudo-likelihood）

PytorchによるRBMの実装

必要なライブラリをインポート

サンプルデータを読み込む

データをPyTorch専用のDatasetを変換するコード

RBMの実装

MNISTを使用した数値実験

参考資料

参考文献

ボルツマンマシン (シリーズ 情報科学における確率モデル 2)

機械学習スタートアップシリーズ これならわかる深層学習入門

深層学習 (機械学習プロフェッショナルシリーズ)

参考論文

まとめ

【Python】マルコフ連鎖モンテカルロ法の応用｜二次元イジング模型

モンテカルロ法の基本をわかりやすく説明してみた｜マルコフ連鎖モンテカルロ法（MCMC...

【入門】データ同化・状態空間モデルをわかりやすく説明してみた

【Python】棄却サンプリングの実装と理論

【入門】グラフィカルモデルと統計的機械学習（マルコフ確率場）

【初心者】趣味ブログで月10万円稼ぐ方法｜好きなことを書いて稼ぐ！

【最新】ブログの始め方ガイド｜ブログ作成方法から収益化まで解説！

【暴露】ブログを始める6つのメリット・3つのデメリット｜東大生が解説！

【東大生が解説】大学生がブログで月10万円稼ぐための15ステップ

【東大生が解説】勉強ブログで収益化（月10万円稼ぐ5ステップ）｜ ノートの代わりにブログにまとめて収益化！

【東大院生が厳選】量子力学のおすすめ参考書10選｜レベル別に徹底解説 ！

【東大院生が厳選】力学・解析力学のおすすめ参考書10選｜レベル別に徹底解説 ！

【東大院生が厳選】微積分（解析学）のおすすめ参考書10選｜レベル別に徹底解説 ！

トップページ

【東大院生が厳選】電磁気学のおすすめ参考書10選｜レベル別に徹底解説 ！

ボルツマンマシン (シリーズ情報科学における確率モデル 2)

機械学習スタートアップシリーズ　これならわかる深層学習入門

【東大生が解説】勉強ブログで収益化（月10万円稼ぐ5ステップ）｜ノートの代わりにブログにまとめて収益化！

【東大院生が厳選】量子力学のおすすめ参考書10選｜レベル別に徹底解説！

【東大院生が厳選】力学・解析力学のおすすめ参考書10選｜レベル別に徹底解説！

【東大院生が厳選】微積分（解析学）のおすすめ参考書10選｜レベル別に徹底解説！

【東大院生が厳選】電磁気学のおすすめ参考書10選｜レベル別に徹底解説！