二項分布の性質(平均・分散・生成関数・ラプラスの極限定理)

二項分布の性質(平均・分散・生成関数・ラプラスの極限定理)
正規分布の次によく出てくる『二項分布』の性質をまとめてみました。
二項分布は、統計を利用する分野では必ず出てくる重要な確率分布の1つです。
私は、それ以上に二項分布の平均や分散をモーメント生成関数からエレガントに導出するのが良い練習になり、
『二項分布』と『生成関数』について理解を深める良いきっかけになると思います。
『モーメント生成関数?』という人は必ず下記を参考にしてください

この記事では、二項分布の性質を数式と図を使いながら解説していきます。
*(iphone・Androidの方へ)数式はスクロール可能です。
二項分布とは

試行の結果が排反な2つの事象のみで、一方の結果Aが出る確率がpの時、試行をN回行って、Aがn回出る確率は以下のように書けます
この確率分布を二項分布(ベルヌーイ分布)という。
排反な事象が2つしかない時というのは決してレアなケースではなく、『成功か失敗』しかない試行をN回すれば二項分布になる。
統計などの教科書で二項分布を\( B(n, p) \)または\(Bin(n, p ) \)と書くことがあります。
参考程度に覚えておいてください。
具体的にコインを100回投げた時の確率分布をPythonで図示したもを以下に示す。
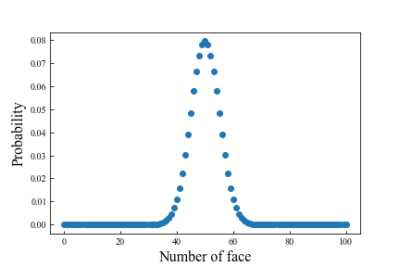
このグラフを書くためのコードは下記に示します。
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["xtick.direction"] = "in"
plt.rcParams["ytick.direction"] = "in"
plt.rcParams["font.family"] = "Times New Roman"
p = 0.5 #コインを投げて表がでる確率
n = 100 #コインを投げる試行の回数
x = range(int(n) + 1) #プロット範囲
binomial = binom.pmf(x, n, p)
#グラフを作成
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, binomial, 'o')
ax.set_ylabel("Probability", fontsize = 16)
ax.set_xlabel("Number of face", fontsize = 16)
plt.show()
fig.savefig("binomial.png")
*試行回数や確率を変化させて遊んで見てください
『Pythonによるグラフの書き方』を知りたい人は下記を参考にしてください

二項分布の全事象について

二項分布の全事象は1(確率の公理)になるはずですが、確認のために計算してみましょう。
$$ \sum_{n = 0}^{N} p_{N}(n) = \sum_{n = 0}^{N} {}_{N} C_{n} p^{n} (1 – p)^{N-n} $$
二項定理から
$$ \sum_{n = 0}^{N} {}_{N} C_{n} p^{n} (1 – p)^{N-n} = (p + 1 – p )^{N} = 1 $$
無事に確認することができました。
二項分布のモーメント生成関数
二項分布の平均と分散を求めるためにモーメント生成関数を計算していきましょう。
二項定理を使うともっと綺麗にまとめることができます
$$ M(\xi) = (1 – p + p e^{\xi} )^{N} $$
『モーメント生成関数』について詳しく知りたい人は下記を参考にしてください。

二項定理の平均と分散

次に、モーメント生成関数を用いて二項分布の平均と分散を求めていきます。
- 二項分布の平均
- 二項分布の分散
① 二項分布の平均
モーメント生成関数\( M(\xi) \)が求められているので平均を求めることは簡単です。
$$ \langle n \rangle = \left. \frac{d M(\xi)}{d \xi} \right|_{\xi = 0} $$
を計算すれば平均が出せます。
$$ \langle n \rangle = \left[ N p e^{\xi} (1 – p + p e^{xi} )^{N – 1} \right]_{\xi = 0} = Np $$
ゆえに二項分布の平均は \(Np\)になることがわかりました。
② 二項分布の分散
分散を計算するために\( \langle n^{2} \rangle \)も導出します。
$$ \langle n^{2} \rangle = \left. \frac{d^{2} M(\xi)}{d \xi^{2}} \right|_{\xi = 0} $$
同様に計算すると
$$ \langle n^{2} \rangle = Np + N (N-1) p^{2} $$
これらから分散を導出すると
$$ \langle ( n – \langle n \rangle )^{2} \rangle = \langle n^{2} \rangle – \langle n \rangle^{2} = N p (1-p) $$
ゆえに分散は \( N p ( 1 – p ) \)と求まりました。
二項分布を正規分布で近似する(ド・モアブル – ラプラスの定理)

二項分布は、nが十分大きいと扱いにくいので扱いやすい正規分布で近似することがあります。
この近似を『ド・モアブル – ラプラスの定理』を言います
詳しくは示しませんが、二項分布 \( B(n, p) \)に従う確率変数について nが十分大きいときに以下の近似が成り立ちます。
スターリングの公式などを使って示すことができます
スターリングの公式とは以下の関係式です
$$ n ! \approx n^{n} e^{-n} \sqrt{2 \pi n} $$
参考資料(二項分布)
参考サイト

参考文献
まとめ
二項分布とは以下のように書ける確率分布です。
$$ p_{N}(n) = {}_{N} C_{n} p^{n} (1 – p)^{N-n} ~~~ (n = 0,1, \cdots N) $$
この確率分布の平均と分散はモーメント母関数により求めることができました。
- モーメント母関数:\( ( 1 – p + p e^{\xi} )^{N} \)
- 平均:\( Np \)
- 分散:\( N p (1 – p) \)
また、二項分布は正規分布に近似することが可能でした(ド・モアブル – ラプラスの定理)。
より詳しく物理数学を学びたい人は下記を参考にしてください


『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。