【入門】WassersteinGANの理論を解説

本記事では、Wasserstein GANの理論的な内容を簡潔に説明します。

イメージがつきにくいWasserstein距離（Earth-Mover距離）が理解できるように解説しました！

＊間違いがあったら本記事のコメント欄または、私のTwitter（努力のガリレオ）にDMよろしくお願いします！！

KL・JS ダイバージェンスの問題点
- 勾配消失が生じる簡単な具体例
Wasserstein距離（Earth-Mover距離）について
Wasserstein GAN
学習のテクニック
まとめ

KL・JS ダイバージェンスの問題点

通常のGANはデータの真の分布$p_{\mathrm{data}}(\mathbf{x})$と学習モデル$q(\mathbf{x}; \theta_{g})$の間のJSダイバージェンスを最小化することで学習を行います。

しかし、JSダイバージェンスを使用する方法は以下のような問題点を持っています。

真の分布と学習モデルの分布が重ならないとき、勾配消失問題が生じる
学習が不安定化する

特に、JSダイバージェンスを利用した学習は、確率分布が重ならないときに勾配消失が生じます。

通常のGANの理論の記事は下記を参考にしてください。

敵対的生成ネットワーク（GAN）の理論を解説敵対的生成ネットワークの必要最低限の理論を解説しました。特にGANの目的関数の気持ちと最適化アルゴリズムの正当性に関して詳しく解説しました。ぜひ参考にしてください。...

勾配消失が生じる簡単な具体例

二つの確率分布が重ならず、勾配消失・発散が起きてしまう具体的な例を紹介します。

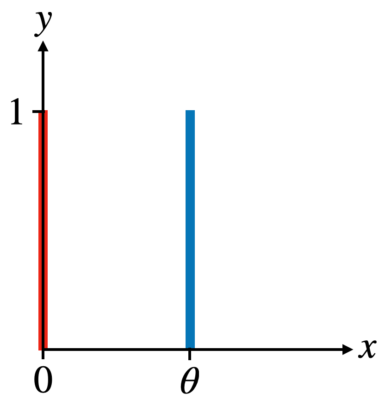
二次元平面上の以下のような確率分布を具体例として紹介します。

具体例 :

$P$ : $ (x = 0, y\sim U(0, 1)$
$Q$ : $ (x = \theta, y \sim U(0, 1)$

ここで、$U(0, 1)$は0〜1の一様分布を表す。

具体的に可視化すると以下のような分布になります。

このときKLダイバージェンスとJSダイバージェンスを具体的に計算すると以下のようになります。

KLダイバージェンス

$\theta \neq 0$のとき

\begin{align} \mathrm{D}_{\mathrm{KL}}(P \mid Q) &= \sum_{x=0, y\sim U(0, 1)} 1 \cdot \log \frac{1}{0} = \infty \\ \mathrm{D}_{\mathrm{KL}}(Q \mid P) &= \sum_{x=\theta, y\sim U(0, 1)} 1 \cdot \log \frac{1}{0} = \infty \end{align}

$\theta = 0$のとき

$$\mathrm{D}_{\mathrm{KL}}(P \mid Q)=\mathrm{D}_{\mathrm{KL}}(Q \mid P)=0$$

JSダイバージェンス（$\theta \neq 0$のとき）

$\theta \neq 0$のとき

\begin{align}\mathrm{D}_{\mathrm{JS}}(P, Q) &= \frac{1}{2} \left(\sum_{x=0, y\sim U(0,1)}1 \cdot \log \frac{1}{1/2} + \sum_{x=\theta, y\sim U(0,1)}1 \cdot \log \frac{1}{1/2} \right) \\ &= \log 2 \end{align}

$\theta = 0$のとき

$$\mathrm{D}_{\mathrm{JS}}(P, Q) = 0$$

JSダイバージェンスの計算結果をプロットとすると以下のようになります。

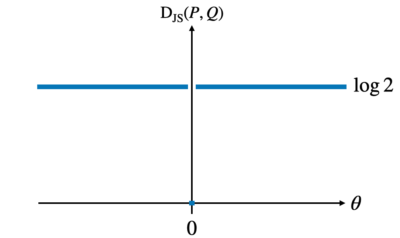
真の分布と学習モデルの分布が一致しない場合、JSダイバージェンスは一定の値となり、勾配が$0$となってしまいます。

そのため学習モデルが真の分布と重ならない場合、勾配が消失して学習することができません。

学習モデルに幅の広いガウス分布に従うノイズ項を加えることで真のデータとの重なりを作ることはできますが、そのノイズ自体が、得られるサンプルの質を落とすことが知られています。

Wasserstein距離（Earth-Mover距離）について

ここでは、Wasserstein GANを理解するために必要なWasserstein距離（Earth-Mover距離）について説明します。

まずは、離散的な最適輸送問題の例を紹介して、連続化することでwasserstein距離の理解を目指します。

最適輸送の設定

まずは、ある地点$P$から地点$Q$への荷物の輸送コストを最適にする問題を考えます。

具体的な設定を以下にまとめておきます。

問題の設定

地点$P$ : 各場所$1, \ldots, m$に、重さ$P_{1}, \ldots, P_{m}$の荷物が積まれている
地点$Q$ : 各場所$1, \ldots, n$に、重さ$Q_{1}, \ldots, Q_{n}$の荷物が積まれている
輸送コスト $d_{ij}$ : 単位量あたりの荷物を地点$P$の場所$i$から地点$Q$の場所$j$に移動するコストを$d_{ij}$とする（コストの例: 移動距離や移動にかかる燃料）
輸送量 $\Gamma_{ij}$ : 地点$P$の場所$i$から地点$Q$の場所$j$に輸送する荷物の輸送量を$\Gamma_{ij}$とする

これらの量から最適輸送問題を定式化します。

定義 : 最適輸送問題

$P$地点から$Q$地点への輸送コストを最小にする最適輸送法を求める問題

具体的には、以下の制約のもとで、\総コスト$C(\Gamma)$を最小化する問題

任意の$j$に対して、$\sum_{j=1}^{n} \Gamma_{ij} = P_{i}$
任意の$i$に対して、$\sum_{i=1}^{m} \Gamma_{ij} = Q_{j}$

$$C(\Gamma) = \sum_{i=1}^{m} \sum_{j=1}^{n} d_{ij} \Gamma_{ij}$$

やや天下り的ですが、最適輸送となる最小コストを使用して、$(P_{1}, \ldots, P_{m})$と$(Q_{1}, \ldots, Q_{n})$の距離を以下のように定義します。

定義 : 輸送距離

$$D(P, Q) = \min_{\Gamma \sim \mathcal{G}} \sum_{i=1}^{m} \sum_{j=1}^{n} d_{ij} \gamma(i, j)$$

ここで、$\mathcal{G}$は$\gamma$の取りうる集合を表し、$\gamma(i,j)$は以下のように定義した。

$$\gamma(i, j) = \frac{\Gamma_{ij}}{\sum_{i=1}^{m} \sum_{j=1}^{n} \Gamma_{i, j}}$$

$\gamma(i, j)$は、荷物の総量に依存しないように正規化を行いました。

このように正規化を行うと、$\gamma(i, j)$は$(i, j)$の結合確率と解釈することができます（すなわち、地点$i$から$j$への輸送率）

この正規化に合わせて、$P$, $Q$の荷物の量を正規化して以下を定義します。

\begin{align} p(i) &= \frac{P_{i}}{\sum_{i^{\prime}} P_{i^{\prime}}} \\ q(i) &= \frac{Q_{j}}{\sum_{j^{\prime}}Q_{j^{\prime}}} \end{align}

また、最適輸送問題の定義から離散確率分布$p(i)$と$q(j)$に以下の関係が成立することがわかります。

\begin{align} \sum_{j=1}^{n} \gamma(i, j) &= \frac{P_{i}}{\sum_{i} P_{i^{\prime}}} \equiv p(i) \\ \sum_{i=1}^{m} \gamma(i,j) &= \frac{Q_{j}}{\sum_{j^{\prime}} Q_{j^{\prime}}} \equiv q(j) \end{align}

この結果から、離散確率分布$p$と$q$の距離は以下のように表すことができます。

$$D[p, q] = \min_{\gamma \in \mathcal{G}} \mathbb{E}_{(i,j) \sim \gamma} [d_{ij}]$$

この考え方を連続の確率分布に拡張したのがWasserstein距離になります。

Earth-Mover距離（Wasserstein距離）最小化による定式化

先程の最適輸送問題を連続確率分布に拡張したものがWasserstein距離になります。

具体的には、二つの確率分布$p$, $q$を考えます。

以下を満たすような同時確率分布$\gamma$を考えます。

\begin{align} \int \gamma(x, y) dx &= p(x) \\ \int \gamma(x, y) dy &= q(y) \end{align}

このような結合分布の集合を$\Pi(p, q)$とします。

この結合分布を使用してWasserstein距離は以下のように定義されます。

定義 : Wasserstein距離（Earth-Mover 距離）

$$W(p, q) = \inf_{\gamma \in \Pi(p, q)} \mathbb{E}_{(x, y) \sim \gamma } \left[\| x – y \| \right]$$

Wassestein距離の具体的な計算

JSダイバージェンスやKLダイバージェンスの計算例で使用した以下の確率分布を使用してWasserstein距離を計算してみます。

このWasserstein距離を計算すると以下のようになります。

$$W(P, Q) = |\theta|$$

$\theta$に関して線形に変化するため勾配消失の問題は生じません。

Kantorovich-Rubinstein双対性

Wasserstein距離を定義通り使用しようと思うと、結合分布$\gamma$の集合$\mathcal{G}$からノルムを最小にするようなものを見つける問題となり、扱いにくいです。

そこで、Kantorovich-Rubinstein双対性という以下の性質を利用します。

Kantorovich-Rubinstein双対性

Wasserstein距離は以下のように表せる。

$$W(p, q) = \sum_{\|f\|_{L} \le 1} \left\{\mathbb{E}_{p}[f(x)] – \mathbb{E}_{q}[f(y)] \right\}$$

ここで、$\|f\|_{L} = 1$は、関数$f$が$1$-Lipschitz関数であること意味しています。

$1$-Lipshitz関数であるとは以下を満たすことを意味します。

$$\forall x, x^{\prime} \in \mathcal{X},~~|f(x) – f(x^{\prime})| \le 1 \times \|x- x^{\prime}\|$$

この結果は、Wasserstein距離の最適化問題は、線形計画法を解くことに対応するので、その双対表現から上記の性質が成り立ちます。

Wasserstein GAN

ここまで、Wasserstein距離の説明をしてたので、簡単にWasserstein GAN（WGAN）を理解することができます。

さっそく、説明していきます。

Wasserstein GANの定式化

一般的なGANの学習で使用するJSダイバージェンス最小化をWasserstein距離の最小化として定式化したものがWasserstein GANです。

具体的には、以下のように定式化されます。

Wasserstein GAN

Wasserstein GANは、以下のWasserstein距離を最小化するように学習モデルを学習するモデルである。

$$\min_{\theta} \max_{\theta_{c}: \|f\|_{L} \le 1} \mathbb{E}_{x \sim p_{\text{data}}(\mathbf{x})} \Big[f(\mathbf{x}; \theta_{c})\Big] – \mathbb{E}_{\mathbf{x}\sim q(\mathbf{x};\theta_{g})} \Big[f(G(\mathbf{z}; \theta_{g}) ; \theta_{c}) \Big]$$

このリプシッツ連続な関数$f$は、ニューラルネットワーク等で構成します。

また、リプシッツ連続な関数$f$は、識別器ではなく『クリティック（Critic）』と呼ばれます。

クリティックの出力はsigmoid活性化関数のように0〜1の出力ではなく、リプシッツ連続な関数$f$の連続的な出力となることに注意してください。

重みベクトルのクリッピング（Cliping）

クリテック（Critic）の重みパラメータは、Lipshitz定数に制約を満たしながら最適化を行う必要があり、一般的には困難です。

そこで、リプシッツ定数に制約を置きながら最適化する代わりに、単純に重みパラメータ$\mathbf{w}$を、ある定数$c$の間にクリッピングすることで制約の実現を目指します。

訓練は安定しますが、クリップ範囲を決める定数$c$を適切に定める必要があります。

重みパラメータのクリッピングは、勾配爆発や、小さい値にクリッピングしすぎることで生じる勾配消失の問題が生じます。

そのためクリッピングの代わりに、勾配のノルムに制限項を加えてリプシッツ連続を再現する方法もあります（WGAN-gp）

具体的には、Real DataとFake Dataの線形補完により、中間データを以下のように作成します。

$$\hat{\mathbf{x}} = \epsilon \mathbf{x}_{\mathrm{real}} + (1 – \epsilon) \mathbf{x}_{\mathrm{fake}}$$

ここで、$\epsilon \sim U[0, 1]$となります。

この中間データを使って以下のような正則化を追加します。

$$\lambda \left(\|\nabla_{\hat{\mathbf{x}}} f_{\mathbf{w}}(\hat{\mathbf{x}}) \|_{2} – 1 \right)^{2}$$

本来なら、任意の$\mathbf{x}$に対してリプシッツ連続が成り立っている必要がありますが、全ての範囲でリプシッツ連続性を満たすのは難しいので、中間データに対してリプシッツ連続が成り立つような正則化を加えています。

Wasserstein GANの学習アルゴリズム

Wasserstein GANは一般的に以下の勾配上昇は以下のようになります。

Wasserstein GANの学習アルゴリズム

以下を$\theta$が収束するまで繰り返す。

$w$の最大化 : 適当な回数繰り返す（勾配が消えないから最適状態近傍まで学習してOK）
- $P$からミニバッチ学習サンプル$\{x^{(i)}\}_{i=1}^{m}$を取得
- $p(z)$からミニバッチ分のサンプル$\{z^{(i)}\}_{i=1}^{m}$を取得
- $w$に関する勾配を計算
  $$g_{w} \leftarrow \nabla_{w} \left[ \frac{1}{m} \sum_{i=1}^{m} f_{w}(x^{(i)}) ~- \frac{1}{m} \sum_{i=1}^{m} f_{w}(g_{\theta}(z^{(i)})) \right]$$
- $w$を更新 : $\eta$は学習率
  $$w \leftarrow \eta g_{w}$$
- $w$をクリッピング
  $$w \leftarrow \mathrm{clip}(w, -c, c)$$
$\theta$の最小化 : 適当な回数繰り返す
- $p(z)$からミニバッチ分のサンプル$\{z^{(i)}\}_{i=1}^{m}$を取得
- $\theta$に関する勾配を計算
  $$g_{\theta} \leftarrow – \nabla_{\theta} \frac{1}{m} \sum_{i=1}^{m} f_{w}(g_{\theta}(z^{(i)}))$$
- $\theta$を更新 :
  $$\theta \leftarrow \eta g_{\theta}$$