ヘッセ行列による多変数関数の極値判定

ヘッセ行列による多変数関数の極値判定
実は、多変数関数の極値問題は、通常の1変数関数と異なり増減表を用いて、極値の判定ができません。
本記事では、多変数関数の極値問題を『ヘッセ行列』と呼ばれる行列を導入して、極小・極大の判断を行う方法を紹介します。
数式とイメージが一致するように、グラフを用いて解説するので安心してください。
ヘッセ行列とは

まずは、ヘッセ行列の定義を以下に示します。
定義 : ヘッセ行列
\(n\)変数関数\(f(x_{1}, x_{2}, \ldots, x_{n})\)に対して、以下の行列\(H\)をヘッセ行列という。
$$H \equiv \left( \begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2}f}{\partial x_{1} \partial x_{2}} & \ldots & \frac{\partial^{2}f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2}f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2}f}{\partial x_{2}^{2}} & \ldots & \frac{\partial^{2}f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2}f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2}f}{\partial x_{n} \partial x_{2}} & \ldots & \frac{\partial^{2}f}{\partial x_{n}^{2}} \end{array} \right) $$
分野によっては、\(f\)のヘッセ行列を\(\nabla^{2}f(x_{1}, \ldots, x_{n})\)と表すこともあります。
行列の正定値性
次に、行列の正定値性という概念を説明します。
以下に、行列の正定値性の定義を示します。
定義 : 行列の正定値性
以下のいずれかを満たす行列\(A\)を正定値行列と呼ぶ。
- 任意のゼロベクトルでない\(\mathbf{x}\)に対して、\(\mathbf{x}^{\top} A \mathbf{x}\)が正
- \(A\)の固有値が全て正
- ある正則行列\(S\)を用いて、\(A = SS^{\top}\)と表せる
- ある直交行列\(Q\)と対角要素が正の対角行列\(\Sigma\)を用いて、\(A = Q\Sigma Q^{\top}\)と表せる
- \(A\)の全ての首座小行列の行列式が正となる
たくさんの条件が出てきて混乱したと思いますが、基本的には、②と⑤の性質を多変数の極値問題では利用することが多いです。
多変数関数の極値判定方法

ここまでで準備が整ったので、多変数関数の極値判定方法に関する性質を以下にまとめます。
- 極値となるための必要条件 : \(f(\mathbf{x})\)が点\(\mathbf{x}\)で極値ならば、点\(\mathbf{x}\)の偏微分の値が全てゼロとなる。
- 極小となるための十分条件 : 点\(\mathbf{x}\)の偏微分の値が全てゼロかつヘッセ行列が正定値ならば、\(\mathbf{x}\)は極小である。
- 極大となるための十分条件 : 点\(\mathbf{x}\)の偏微分の値が全てゼロかつヘッセ行列が負定値ならば、\(\mathbf{x}\)は極大である。
多変数関数の極値の候補の見つけ方
ここまでの性質から、多変数関数の極値の候補の見つけ方をまとめます。
具体的には、以下の手順で極値の候補を見つけます。
- 偏微分が\(0\)となる点を見つける
- ヘッセ行列を計算
- ヘッセ行列の正定値性を確認
以下では、二変数を極値を探索しましょう。
① : 偏微分が\(0\)となる点を見つける
まず、各変数の偏微分を求めて極値の候補を見つけます。
\begin{align} \frac{\partial f}{ \partial y } &= x~ – \frac{8}{y^{2}} = 0 \\ \frac{\partial f}{ \partial x } &= y~ – \frac{8}{x^{2}} = 0 \end{align}
この方程式を解くと、以下の解が得られます。
$$ (x , y) = (2, 2) $$
② : ヘッセ行列を計算
ヘッセ行列を求めるために、二階微分を計算していきます。
二階微分の結果は以下のようになります。
$$H = \left( \begin{array}{cc} \frac{16}{x^{3}} & 1 \\ 1 & \frac{16}{y^{2}} \end{array} \right)$$
次に極値の候補を計算して代入するとヘッセ行列は以下のようになります。
$$ H = \left( \begin{array}{cc} 2 & 1 \\ 1 & 2 \end{array} \right) $$
③ : ヘッセ行列の正定値性を確認
上で求めたヘッセ行列の固有値を計算すると固有値は、以下のようになります。
$$ ( \lambda_{1}, \lambda_{2} ) = (1, 3) $$
ヘッセ行列の全ての固有値が正なので、極値の候補である \( (2, 2) \)は、極小値となります。
最後にまとめると、\((2, 2)\)のとき極小値 \(f(2, 2) = 12 \)となります。
実際にグラフを書いてみた
ヘッセ行列で極値が求められているか確認するために
実際にグラフを書いてみました。
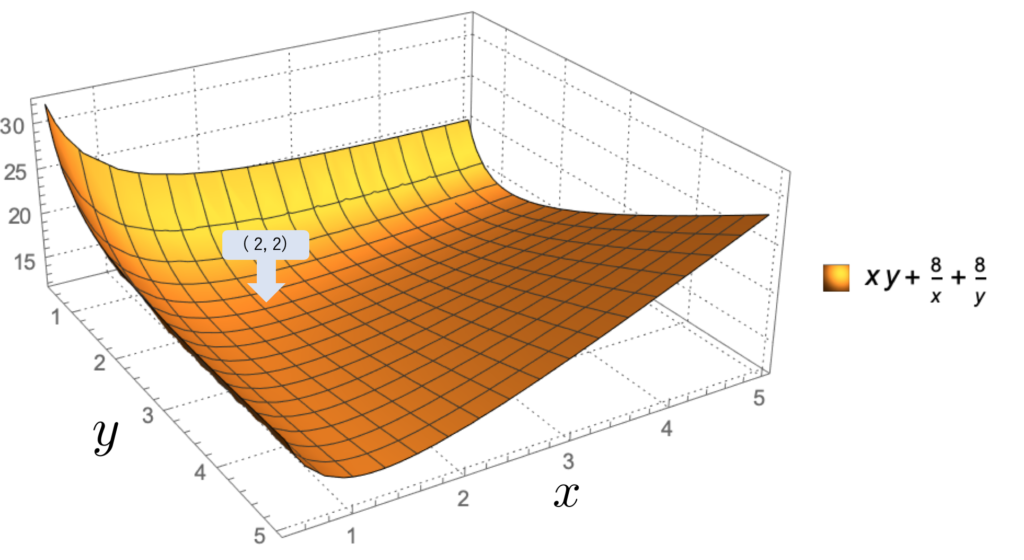
グラフから、\( (2, 2) \)の時に極小値になっていることがわかります
ヘッセ行列は、確かに極値判定に使えることがわかりましたね!
まとめ
多変数関数の極値を判定するためには、ヘッセ行列が有効です。
具体的に多変数関数の極値を求める手順は、以下の通りです。
- 偏微分が\(0\)となる点を見つける
- ヘッセ行列を計算
- ヘッセ行列の正定値性を確認
まとめてみると意外と簡単ですね。
皆さんも、手を動かして練習問題を解いてみましょう!

『Amazon Prime Student』は、大学生・大学院生限定のAmazon会員制度です。
Amazonを使用している方なら、必ず登録すべきサービスといっても過言ではありません…
主な理由は以下の通りです。
- 『Amazon Prime
』のサービスを年会費半額で利用可能
- 本が最大10%割引
- 文房具が最大20%割引
- 日用品が最大15%割引
- お急ぎ便・お届け日時指定便が使い放題
- 6ヶ月間無料で使用可能
特に専門書や問題集をたくさん買う予定の方にとって、購入価格のポイント10%還元はめちゃめちゃでかいです!
少なくとも私は、Amazon Prime Studentを大学3年生のときに知って、めちゃめちゃ後悔しました。
専門書をすでに100冊以上買っていたので、その10%が還元できたことを考えると泣きそうでした…ww
より詳しい内容と登録方法については下記を参考にしてください。

登録も退会もめちゃめちゃ簡単なので、6ヶ月の無料体験期間だけは経験してみても損はないと思います。