【Python】Annealed Importance Sampling(焼きなまし重点サンプリング)の解説と実装

本記事では、Annealed Importance Sampling(焼きなまし重点サンプリング)の解説と実装を紹介します。
Annealed Importance Sampling(焼きなまし重点サンプリング)

Importance Sampling(重点サンプリング)は、目的の確率分布\(p(x)\)とは別にサンプリングが容易な提案分布\(q(x)\)を用いて、確率分布\(p(x)\)の期待値や規格化定数を推定する方法です。
もし、Importance Sampling(重点サンプリング)についてご存知でない方は先に下記の記事を一読してから本記事を読んでいただけると幸いです。

重点サンプリングでは、提案分布\(q(x)\)が目的の確率分布\(p(x)\)と似たような分布であることが重要であり、似ていない分布を用いると推定値の分散が大きくなり、推定精度が悪化します。
しかし、サンプリングが用意で確率分布\(p(x)\)と似たような分布\(q(x)\)を用意することは容易ではありません。
その問題を解決するのが、本記事で紹介するAnnealed Importance Sampling(焼きなまし重点サンプリング)です。
まずは、問題設定を簡単に説明した後にアルゴリズムの内容を説明をします。
問題設定
規格化定数が未知の確率分布\(p_{K}(x)\)の規格化定数やその期待値(統計量)を知ることを目的とします(Kは後の表記を簡単にするためのインデックスです。この段階ではあまり気にしないでください)
以降、その確率分布\(p_{K}(x)\)を規格化定数\(Z_{K}\)とそれ以外の部分に分けて次のように記述することにします。
$$p(x) = \frac{1}{Z_{K}} f_{K}(x)$$
ここで、規格化定数は、以下の条件を満たすように設定しいます。
$$Z_{K} = \int f_{K}(x) dx$$
今回は、連続確率分布を扱っていますが、離散確率分布でも以降の導出は容易です。
Annealed Importance Sampling(AIS)側の確率分布
まずは、Importance samplingと同様に、規格化定数が既知(または計算が容易な規格化定数)で、サンプリングすることが容易な近似分布\(p_{0}(x)\)を準備します。
$$p_{0}(x) = \frac{1}{Z_{0}} f_{0}(x)$$
再度強調しますが、この規格化定数\(Z_{0}\)は、既知または計算が容易な分布を使用しましょう。また、\(p(x)\)と\(p_{0}(x)\)は必ずしも類似した分布である必要はありません。
さらに、AISでは以下のような中間分布を準備します。
$$p_{k}(x; \beta_{k}) = \frac{1}{Z_{k}} f_{0}(x)^{\beta_{k}} f(x)^{1-\beta_{k}}$$
中間分布と呼んでいる理由は、パラメータが\(\beta_{k} = 0\)のときは近似分布\(p_{0}\)になり、パラメータが\(\beta_{k} =1\)のときにはターゲットの分布\(p_{K}\)となることに起因します。
中間分布のパラメータは、ユーザーが決定する量で次の性質を満たすように設定します。
$$0 = \beta_{0} < \beta_{1} < \cdots < \beta_{K-1} < \beta_{K} =1$$
規格化定数と期待値の計算方法
AISは規格化定数の比\(Z_{k+1}/Z_{k}\)が次のように表せることを利用します。
\begin{align} \frac{Z_{k+1}}{Z_{k}} &= \frac{1}{Z_{k}} \sum_{x}f_{k+1}(x) \\ &= \mathbb{E}_{p_{k}}\left[\frac{f_{k+1}(x)}{f_{k}(x)} \right] \\ &= \lim_{M \to \infty} \frac{1}{M} \sum_{m=1}^{M} \frac{f_{k+1}(x_{k}^{m})}{f_{k}(x_{k}^{m})} \end{align}
ここで、\(x_{k}^{(m)}\)は、確率分布\(p_{k}\)に従うサンプル列の\(m\)番目のサンプルを表すことにします。
この性質を使用すると以下の等式を得ることができます。
\begin{align} \frac{Z_{K}}{Z_{0}} &= \frac{Z_{1}}{Z_{0}} \frac{Z_{2}}{Z_{1}} \times \cdots \times \frac{Z_{K}}{Z_{K-1}} \\ &= \prod_{k=1}^{K} \mathbb{E}_{p_{k}}\left[\frac{f_{k+1}(x)}{f_{k}(x)} \right] \\ &= \frac{1}{M} \sum_{m=1}^{M} \prod_{k}^{K-1} \frac{f_{k+1}(x^{(m)}_{k})}{f_{k}(x^{(m)}_{k})} \\ &= \frac{1}{M} \sum_{m=1}^{M} \frac{f_{1}(x_{0}^{(m)})}{f_{0}(x_{0}^{(m)})}\frac{f_{2}(x_{1}^{(m)})}{f_{1}(x_{1}^{(m)})} \cdots \frac{f_{K}(x_{K-1}^{(m)})}{f_{K-1}(x_{K-1}^{(m)})} \\ &\equiv \frac{1}{M} \sum_{m=1}^{M} \omega^{(m)} \end{align}
ここで、\(\omega^{(m)}\)は重みと呼ばれ、以下のように定義しました。
$$\omega^{(m)} = \frac{f_{1}(x_{0}^{(m)})}{f_{0}(x_{0}^{(m)})}\frac{f_{2}(x_{1}^{(m)})}{f_{1}(x_{1}^{(m)})} \cdots \frac{f(x_{K-1}^{(m)})}{f_{K-1}(x_{K-1}^{(m)})}$$
この重みを使うことでターゲットとなる確率分布\(p_{K}\)に関する\(A(x)\)の期待値を以下のように計算することができます。
$$\mathbb{E}_{p_{K}}\left[ A(x) \right] = \frac{\sum_{m=1}^{M} A(x^{m}_{0}) \omega^{(m)}}{\sum_{m=1}^{M} \omega^{(m)}}$$
また、規格化定数は次のように評価することができます。
$$Z_{K} = \frac{Z_{0}}{M} \sum_{m=1}^{M} w^{(m)}$$
AISのアルゴリズム
規格化定数や期待値の計算方法はわかりましたが、定式化の中には、中間分布から生成されるサンプル列\(\{x_{0}^{(m)}, x_{1}^{(m)}, \ldots, x_{K-1}^{(m)}\}_{m=1}^{M}\)が必要となります。
その部分は、適当な遷移確率を利用して、マルコフ連鎖モンテカルロ法によって生成します。
以下に具体的なアルゴリズムをまとめます。
AISのアルゴリズム
- 入力 : パラメータ列 \(\{\beta_{k}\}_{k=0}^{K}\)
- 以下を\(1 \sim M\)繰り返す
- \(p_{0}\)から\(x_{0}^{(m)}\)をサンプル
- 以下を\(1 \sim K\)回繰り返す
- 初期値を\(x_{k-1}^{(m)}\)として、マルコフ連鎖モンテカルロ法により\(p_{k}(x)\)から\(x_{k}^{(m)}\)をサンプル
- 重みを計算
$$\omega^{(m)} \leftarrow \frac{f_{1}(x_{0}^{(m)})}{f_{0}(x_{0}^{(m)})}\frac{f_{2}(x_{1}^{(m)})}{f_{1}(x_{1}^{(m)})} \cdots \frac{f(x_{K-1}^{(m)})}{f_{K-1}(x_{K-1}^{(m)})}$$
- 規格化定数と\(A(x)\)を以下のように計算
\begin{align} Z_{K} &= \frac{Z_{0}}{M} \sum_{m=1}^{M} \omega^{(m)} \\ \mathbb{E}_{p_{k}} \left[A(x) \right] &= \frac{\sum_{m=1}^{M} A(x^{m}_{0}) \omega^{(m)}}{\sum_{m=1}^{M} \omega^{(m)}} \end{align}
Annealed Importance Sampling(焼きなまし重点サンプリング)の実装例

必要なライブラリをインポート
import numpy as np
from matplotlib import pyplot as plt
import scipy.stats as stats
import seaborn as sns
sns.set()
# SEEDを固定
np.random.seed(0)
問題設定
問題設定を以下にまとめます。
- 目的の確率分布
$$0.5 \times \mathcal{N}(0, 1) + 0.5 \times \mathcal{N}(4, 1)$$
- 既知の情報(目的の確率分布の規格化定数は未知)
$$f_{K}(x) = 0.5 \exp\left( – \frac{(x-4)^{2}}{2} \right) + 0.5 \exp\left(- \frac{x^{2}}{2} \right)$$
- 提案分布
$$f_{0}(x) = \exp \left(- \frac{(x- \mu)^{2}}{2 \sigma^{2}} \right)$$
$$Z_{0} = \sqrt{2 \pi \sigma^{2}}$$
まずは、この問題設定に合うように\(f_{K}(x)\), \(f_{0}(x)\), \(f_{k}(x)\)を実装しましょう。
# target dist
def f_K(x, mu1=0, mu2=4.0, pi=0.5):
pi1 =pi
pi2 =1-pi1
a1 = - ((x - mu1)**(2)) / 2
a2 = - ((x - mu2)**(2)) / 2
return pi1*np.exp(a1)+pi2*np.exp(a2)
# proposal dist
def f_0(x, mu=0, scale=1):
return np.exp(-((x-mu)**2) / 2)
# intermediate dist
def f_k(x, beta):
return (f_0(x)**(1-beta))*(f_K(x)**beta)
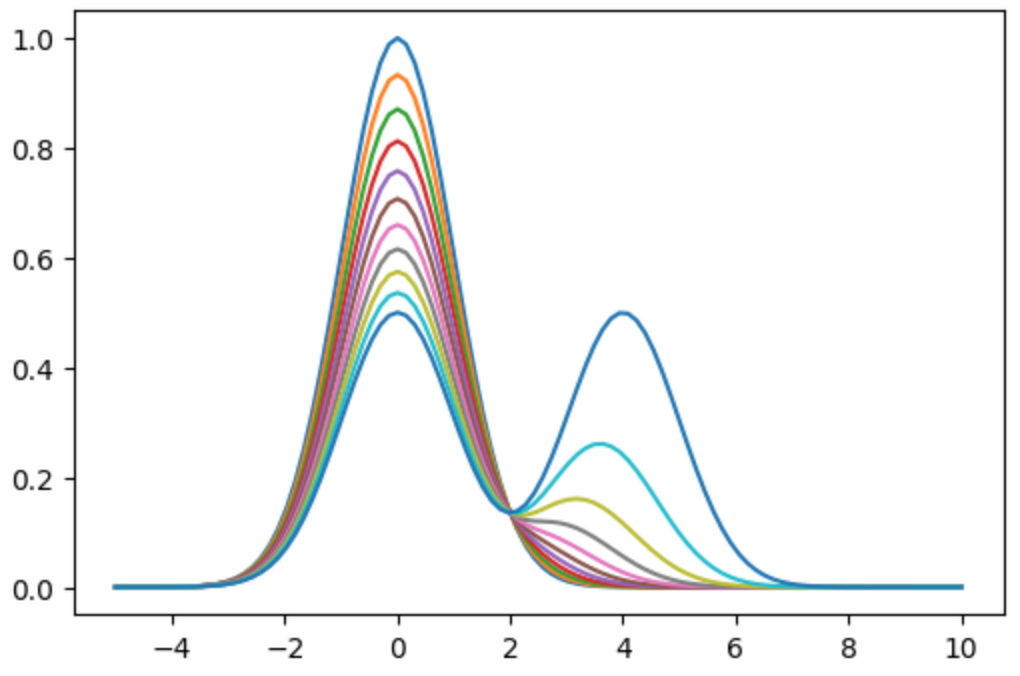
簡単に中間分布・提案分布・目的の分布の関係を図示しておきます。
x_test = np.linspace(-5, 10, 100)
fig, ax = plt.subplots()
for i in range(11):
ax.plot(x_test, f_k(x_test, i/10))
plt.show()
<output>
マルコフ連鎖モンテカルロ法を実装
中間分布からのサンプリングにマルコフ連鎖モンテカルロ法が必要になります。
今回は、メトロポリス法を使用します。
def metropolis(xs_init, beta, steps=10):
# inital condition
xs = xs_init
for i in range(len(xs_init)):
for j in range(steps):
prop_x = xs[i] + np.random.randn()
accept_prob = f_k(prop_x, beta)/f_k(xs[i], beta)
if np.random.rand() <= accept_prob:
xs[i] = prop_x
return xs
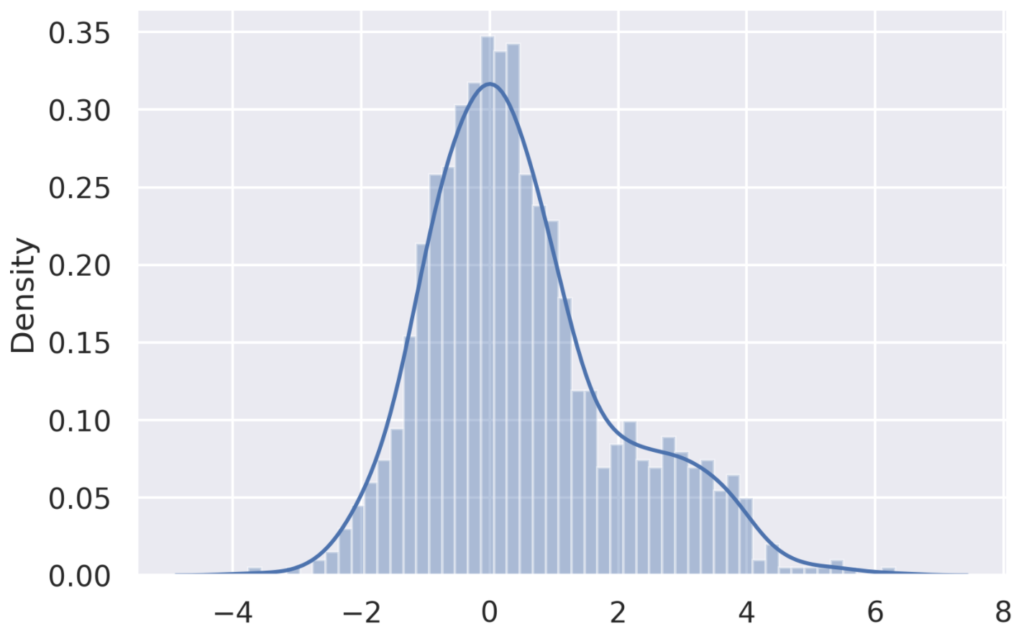
一応、\(\beta_{k}=0.75\)のときにしっかりサンプルが得られているかを確認しておきます。
x_0 = np.random.randn(1000)
xs = metropolis(x_0, 0.75, steps=300)
sns.distplot(xs, bins=50, kde='True')
plt.show()
<output>
Annealed Importance Sampling(焼きなまし重点サンプリング)の実装
これまでのコードを使用して、Annealed Importance Sampling(焼きなまし重点サンプリン)の実装を行います。
def AIS(n_samples=1000, n_inter=100, n_steps=30):
'''
Args:
n_samples : サンプル列の長さ(上述のMに対応)
n_inter : 中間分布の個数
n_steps : MCMCのステップ数
Return:
norm_term : 目的の確率分布の規格化定数の推定値
mean : 目的の確率分布の平均の推定値
'''
# 中間分布のパタメータ
betas = np.linspace(0, 1, n_inter)
xs_k = np.random.randn(n_samples)
# 対数の値で保存(overflowを避けるため)
log_weights = np.zeros(n_samples)
for i in range(1, len(betas)):
log_weights += np.log(f_k(xs_k, betas[i])) - np.log(f_k(xs_k, betas[i-1]))
xs_k = metropolis(xs_k, betas[i], steps=n_steps)
weights = np.exp(log_weights)
# 規格化定数
norm_term = (np.sum(weights)/n_samples)*(np.sqrt(2*np.pi))
# 平均
mean = np.sum(xs_k*weights)/np.sum(weights)
return norm_term, mean
実際に実行してみましょう。
AIS(n_samples=1000, n_inter=300, n_steps=30)
<output>
(2.5075079910242226, 2.060047935888935)
目的の確率分布の規格化定数は、\(\sqrt{2 \pi} = 2.5066282\cdots\)であり、平均値は\(2.0\)であるため、良い推定値が得られていることがわかります。
規格化定数や統計量の計算には、指数関数の和の対数を取る計算が含まれ、頻繁にオーバーフローが生じます。
その場合は、以下のlogsumexp法を使用することで、解決できるケースが多いです。

まとめ
本記事では、Annealed Importance Samplingの理論と実装を紹介しました。
より複雑な確率分布に使用して、遊んでみてください!

Pythonを学習するのに効率的なサービスを紹介していきます。
まず最初におすすめするのは、Udemyです。
Udemyは、Pythonに特化した授業がたくさんあり、どの授業も良質です。
また、セール中は1500円定義で利用することができ、コスパも最強です。
下記の記事では、実際に私が15個以上の講義を受講して特におすすめだった講義を紹介しています。

他のPythonに特化したオンライン・オフラインスクールも下記の記事でまとめています。

自分の学習スタイルに合わせて最適なものを選びましょう。
また、私がPythonを学ぶ際に使用した本を全て暴露しているので参考にしてください。