【簡単】主成分分析の理論とPythonによる実装(寄与率も計算)|アニメーション付き

【簡単】主成分分析の理論とPythonによる実装(寄与率も計算)|アニメーション付き
本記事では、データ分析でたびたび使用される主成分分析の理論と実装を紹介します。
Pythonのsklearnを用いて誰でも簡単に主成分分析ができるようになります!
主成分分析の理論

まず、主成分分析の目的と理論を簡単に説明します。
以下の流れで解説します。
- 主成分分析の目的
- 第一主成分の見つけ方
- 第二主成分以降の見つけ方
- 主成分分析の異なる捉え方
- 主成分分析のまとめ
主成分分析の目的
データ\(\mathcal{D} = \{\mathbf{x}_{1}, \ldots, \mathbf{x}_{M}\}\), ( \(\mathbf{x}_{m} \in \mathbb{R}^{D}\) )が与えられている状況を考えます。
主成分分析の目的は、\(D\)次元のデータをそれよりも低い次元で表して、コンパクトな表現を得ることです。
逆に、主成分分析ではデータの背後にある構造は、より低次元の空間(より詳しくは、線型空間)にあることを仮定しています。
線型空間とはざっくりいうと平坦な座標軸からなる空間とイメージしておけばOKです…
第一主成分の見つけ方
まずは、データをよく表現する1次元空間を見つけることから考えましょう。
このような問題は、1次元空間を表す単位ベクトル\(\mathbf{v}\)の中でデータを最もよく表現する方向を見つける問題に帰着されます。
このような単位ベクトルを第一主成分といいます。
すなわち、以下を満たすような\(\mathbf{v}\)を見つける問題となります。
$$\min_{\|\mathbf{v}\|=1} \frac{1}{N} \sum_{m=1}^{M} \|\mathbf{x}_{m} – (\mathbf{v}^{\top}\mathbf{x}_{m})\mathbf{v}\|^{2}$$
ここで簡単のため、データ\(\mathcal{D}\)の標本平均は、\(0\)になるように処理されていることを仮定します。
二乗を展開して、整理すると以下の最大化問題に帰着することができます。
$$\max_{\|\mathbf{v}\|=1} = \frac{1}{N} \sum_{m=1}^{M} \mathbf{x}_{m}^{\top} \mathbf{v} \mathbf{v}^{\top} \mathbf{x}_{m} = \mathbf{v}^{\top}C\mathbf{v}$$
ここで、\(C\)は、標本平均\(0\)の標本共分散行列を表し、以下のように定義されます。
$$C := \frac{1}{M} \sum_{m=1}^{M} \mathbf{x}_{m} \mathbf{x}_{m}$$
この行列は、\(C^{\top} = C\)という性質を満たすため対称行列と呼ばれる行列の一種です。
そして、一般に対称行列は正規直交ベクトルからなる直交行列で対角化することができます(詳しい説明は、線形代数のおすすめ参考書13選を用いて勉強してみください)
すなわち、この性質から、もとの最小化問題は、\(C\)の最大固有値に対応する固有ベクトルを求める問題に帰着されました。
つまり、最大固有値を\(\lambda_{1}\)とすると、それに対応する固有ベクトルを\(\mathbf{u}_{1}\)とすると、\(\mathbf{v} = \mathbf{u}_{1}\)となります。
データをよく表現する一次元空間は、分散共分散行列の最大固有値に対応する固有ベクトルの方向となることがわかりました。
ここで、標本平均が\(0\)となることを仮定して計算を進めましたが、標本平均が\(0\)とならないケースの計算も容易に行うことができます(ぜひやってみてください!)
しかし、実際のデータ解析で主成分分析を行う場合、各データのスケールを合わせるために標準化を行うことが多いため、本記事で紹介した標本平均が\(0\)となる場合をそのまま適用することが多いです。
第一主成分は分散を最大にする方向!
ここで、\(\mathbf{y}_{k} = \mathbf{v}^{\top} \mathbf{x}_{k}\)と定義すると先程の最大化問題は以下のように変形することができます。
$$\max_{\|\mathbf{v}_{1}\|=1} \mathbf{v}^{\top} C \mathbf{v} = \max_{\|\mathbf{v}_{1}\|=1} \frac{1}{N} \sum_{k=1}^{N} y_{k}^{2}$$
これは、データ\(\mathcal{D}\)を一次元空間上に射影して、射影したデータの分散を最大化するように\(\mathbf{v}\)を選ぶ問題に対応することを意味しています。
つまり、データをよく表現する1次元空間を選ぶことは、データを射影した後に分散が最大となるような方向を選ぶ問題と等価になります。
第二主成分以降の見つけ方
次に考えるのは、\(\mathbf{u}_{1}\)を除いた中で\(M\)個のデータをよく近似する方向を求める方法を考えます。
この問題は以下のように定式化することができます。
$$\min_{\mathbf{v} \perp \mathbf{u}_{1}, \|\mathbf{v}\|=1} \frac{1}{N} \sum_{m=1}^{M} \|\mathbf{x}_{m} – (\mathbf{v}^{\top}\mathbf{x}_{m})\mathbf{v}\|^{2}$$
この問題は同様に、以下の最大化問題に帰着することができます。
$$\max_{\mathbf{v} \perp \mathbf{u}_{1}, \|\mathbf{v}\|=1} \mathbf{v}^{\top} C \mathbf{v}$$
この最大値は、\(\lambda_{2}\)となり、\(\mathbf{v} = \mathbf{u}_{2}\)となります。
以下同様に、『\(\mathbf{u}_{1}, \ldots, \mathbf{u}_{k-1}\)軸方向を除いた空間で\(M\)個のデータをよく近似する方向を見つけなさい』という問題を解くことでデータを任意の空間に近似することができます。
すなわち、『主成分分析をやりなさい=分散共分散行列の固有値問題を解きなさい』ということになります。
寄与率と累積寄与率
主成分分析を行う際に求めた分散共分散行列の固有ベクトルは主成分と呼ばれることを説明しました。
実は、固有値の方は、どの次元まで圧縮するのかを考える指標として利用されます。
具体的には、ある特定の主成分によってデータ全体をどの程度説明できるかを表す以下の寄与率というものを指標として使用します。
$$\mathrm{CR}_{i} = \frac{\lambda_{i}}{\sum_{i=1}^{D} \lambda_{i}}$$
ここで、\(\mathrm{CR}_{i}\)を\(i\)番目の寄与率としました。
そして、その寄与率を用いて第一主成分からある主成分までがデータの全体をどの程度説明できるかを表す量として、以下で定義される累積寄与率を使用します。
$$\mathrm{CCR}_{K} = \sum_{i=1}^{K} \mathrm{CR}_{i}$$
ここで、\(K\)番目の主成分までの累積寄与率を\(\mathrm{CCR}_{K}\)としました。
主成分分析の異なる捉え方(超余談)
ここでは、主成分分析のやや異なる捉えからを説明します。
主成分文分析を用いて\(k\)次元への近似する場合は、以下の問題を解くことで実行します。
正規直交ベクトル\(\mathbf{v}_{1}, \ldots, \mathbf{v}_{k}\)に対して、以下を最小化する問題。
$$\min_{\mathbf{v}_{1}, \ldots, \mathbf{v}_{k}} \frac{1}{M} \sum_{m=1}^{M} \|\mathbf{x}_{m} – (\mathbf{v}_{1}\mathbf{v}_{1}^{\top} + \cdots + \mathbf{v}_{k}\mathbf{v}^{\top}_{k}) \mathbf{x}_{m}\|^{2}$$
この問題は、以下の最大化問題に定式化することができます。
\begin{align}&\max_{\mathbf{v}_{1}, \ldots, \mathbf{v}_{k}} \mathbf{v}_{1}^{\top} C \mathbf{v}_{1} + \cdots + \mathbf{v}_{k}^{\top} C \mathbf{v}_{k}\\ = &\max_{V \in \mathrm{St}(k, n)} \mathrm{tr}V^{\top} C V \\ = &\lambda_{1} + \cdots \lambda_{k} \end{align}
ここで、\(\mathrm{St}(r, n) := \{V \in K^{n \times r} \mid V^{\dagger}V= I_{r} \}\)と定義しました。
余談ですが、\(\mathrm{St}(r, n)\)は、シュティーフェル多様体と呼ばれます。
つまり、主成分分析は、シュティーフェル多様体上の最大化問題となります。
この最大化問題は、\(C\)の正規直交固有ベクトル\(\mathbf{u}_{1}, \ldots, \mathbf{u}_{k}\)を選んだ際に達成されます。
主成分分析のまとめ
ここまでの話をまとめると主成分分析とは、標本分共分散行列\(C\)の固有値\(\lambda_{1} \ge \cdots \ge \lambda_{n} \ge 0\)と正規直交固有ベクトル\(\mathbf{u}_{1}, \ldots, \mathbf{u}_{n}\)を計算して、データをよく近似するような\(r\)を定め各データを以下で近似することと等価です。
$$\tilde{\mathbf{x}}_{k} = (\mathbf{u}_{1} \mathbf{u}_{1}^{\top} + \cdots + \mathbf{u}_{r} \mathbf{u}_{r}^{\top})\mathbf{x}_{k}$$
このとき、\(r\)は累積寄与率によって判断して適切に決定します。
主成分分析の実装|Pythonのsklearnを用いて実装

ここからは、Pythonを利用して手書き数字データ(MNIST)の主成分分析を行なっていきます。
使用するライブラリをインポート
まずは、以下を実行して使用するライブラリをインポートしてください。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# 3次元グラフ作成用
from mpl_toolkits.mplot3d import Axes3D
# MNISTデータのインポート
from keras.datasets import mnist
もしも、numpy, matplotlib, pandasの基本操作が怪しい方は、下記を参考にしてください。
データのインポートと前処理
次にデータをインポートして、平均分散をそれぞれ0, 1に変換する標準化を行います。
# dataのimport
(data, labels), _ = mnist.load_data()
data = data.reshape(-1, 28*28)
# rescale
data = data/255
# 標準化
ss = StandardScaler()
standardized_data = ss.fit_transform(data)
PCAを実行
sklearnのPCAを用いることで簡単にPCAを行うことができます。
pca = PCA()
# PCAを実行
pca.fit(standardized_data)
たったこれだけでPCAを実行できます!!
圧縮したデータを表示
次に主成分分析により得られた主成分を用いてデータを圧縮します。
sklearnでは以下を実行することでデータ圧縮を実行します。
# データの圧縮
feature = pca.transform(standardized_data)
# pandasデータフレームに格納
feature_df = pd.DataFrame(feature, index=df.index, columns=[f"PC{i+1}" for i in range(feature.shape[1])])
<output>
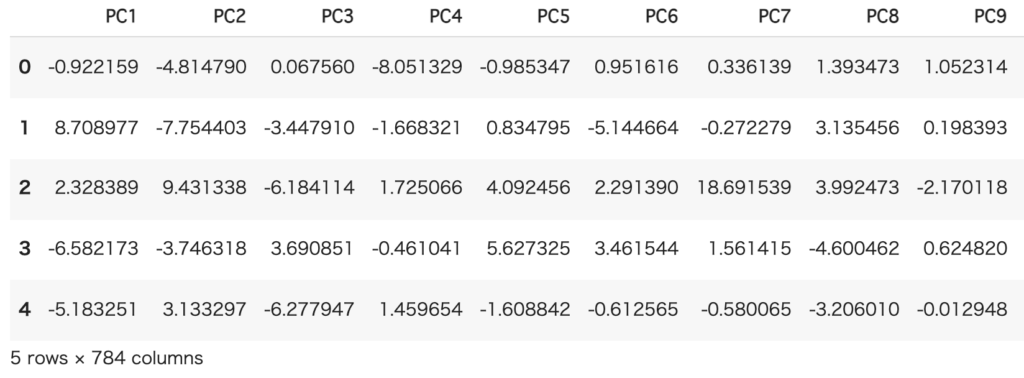 主成分への圧縮結果
主成分への圧縮結果
データ分析の場面では、Dataframe型にして扱うことが多いのでpandasデータフレームに格納するところまで紹介しました。
累積寄与率・寄与率・固有値・固有ベクトルについて
累積寄与率・寄与率・固有値・固有ベクトルは以下を実行することで得ることができます。
# 寄与率
cr = pca.explained_variance_ratio_
# 累積寄与率
ccr = np.add.accumulate(cr)
# 固有値
eigenvalue = pca.explained_variance_
# 固有ベクトル
eigenvector = pca.components_
累積寄与率をプロットしてみます。
fig, ax = plt.subplots()
ax.plot(ccr)
ax.set_ylabel('CCR', fontsize=15)
plt.show()
<output>
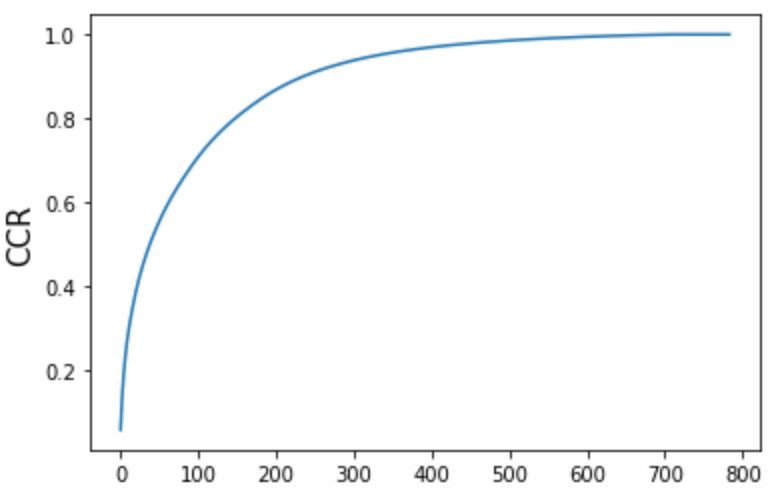 寄与率をプロット
寄与率をプロット
このことから、おおよそ150個くらいの主成分を用いてデータを80%程度圧縮できることがわかりました。
データ圧縮の結果を可視化
第1主成分から第3主成分を用いることでデータがどのように圧縮されるのかを可視化してみました。
fig, ax = plt.subplots(figsize=(8, 8), subplot_kw={'projection' : '3d'})
# 背景色を白色に設定
ax.w_xaxis.set_pane_color((0., 0., 0., 0.))
ax.w_yaxis.set_pane_color((0., 0., 0., 0.))
ax.w_zaxis.set_pane_color((0., 0., 0., 0.))
for label in range(0, 10):
ax.scatter(feature[labels==label][:, 0], feature[labels==label][:, 1], feature[labels==label][:, 2], s=3, label=label)
# 軸ラベルの設定
ax.set_xlabel('PC1', size=15)
ax.set_ylabel('PC2', size=15)
ax.set_zlabel('PC3', size=15)
ax.legend(bbox_to_anchor=(1.0, 1.0), loc='upper left', fontsize=10)
plt.show()
<output>
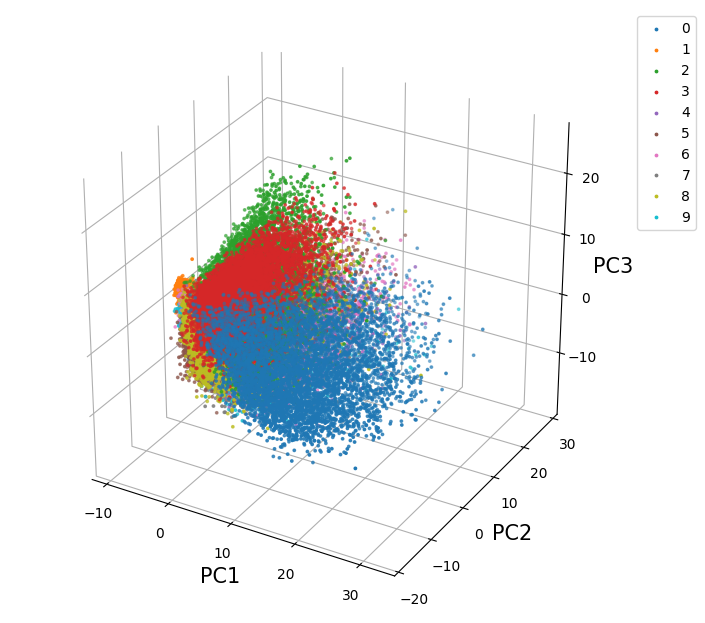 3次元空間への圧縮
3次元空間への圧縮
3次元のみしか利用していないので完全に数字を分けることはできていませんが、大まかにグループ分けがなされているのがわかります。
3次元プロットの作成方法に関しては、下記を参考にしてください。
次は、圧縮したデータからもとのデータを復元してみます。
圧縮したデータからの復元
次に、圧縮したデータを復元してみます。
今回は、累積寄与率が0.5程度となる50個の主成分を用いてデータを復元した結果を示します。
n_pc = 50
pca = PCA(n_components=n_pc)
pca.fit(standardized_data)
# 50次元に圧縮
encoded_data = pca.transform(standardized_data)
# 圧縮した情報から元の画像を復元
decoded_data = pca.inverse_transform(encoded_data)
# 標準化を戻す
decoded_data = ss.inverse_transform(decoded_data)
<output>
 50次元の主成分を用いて圧縮したデータを復元
50次元の主成分を用いて圧縮したデータを復元
また、徐々に1〜200個のまでの主成分を用いて圧縮してから、復元した数字をアニメーションで表示すると以下のようになります。
 徐々に1〜200の主成分を使って復元した様子
徐々に1〜200の主成分を使って復元した様子
matplotlibでアニメーションを作成する方法は、下記を参考にしてください。
参考資料
私が本記事を作成するために使用した資料を共有します。
参考文献
まずは、参考文献を紹介します。
機械学習スタートアップシリーズ これならわかる深層学習入門 (KS情報科学専門書)
タイトルにあるように主成分分析以外にも色々なことを説明しています。
主成分分析と自己符号化機の関係性までまとめていて知見が深まります。
主成分分析自体の解説も超わかりやすいです。
買っておいて損はないですね…
多変量解析法入門 (ライブラリ新数学大系)
多変量解析を体系的に学びたい方はとりあえずこの本!!というくらい有名です。
主成分分析の部分は、特に解説が詳しくてわかりやすいです。
まとめ
本記事では、主成分分析を直感的に理解できるよう説明しました。
実際に実装してみるとsklearnで簡単に実装が可能なこともわかったと思いますが、中身で何をやっているかがわからないと応用は聞きません…
そのためにも、本記事の前半部分をよく読み中身で何をやっていてるのかを理解して使うようにしましょう。
本記事では、これ以外にも機械学習のさまざまなモデルをpythonにより実装を混ぜながら解説しています。
他の機械学習の情報を知りたい方は下記を参考にしてください。

Pythonを学習するのに効率的なサービスを紹介していきます。
まず最初におすすめするのは、Udemyです。
Udemyは、Pythonに特化した授業がたくさんあり、どの授業も良質です。
また、セール中は1500円定義で利用することができ、コスパも最強です。
下記の記事では、実際に私が15個以上の講義を受講して特におすすめだった講義を紹介しています。

他のPythonに特化したオンライン・オフラインスクールも下記の記事でまとめています。

自分の学習スタイルに合わせて最適なものを選びましょう。
また、私がPythonを学ぶ際に使用した本を全て暴露しているので参考にしてください。