【超入門】PyTorchの使い方｜線形回帰から基本を学ぶ！

PyTorchの使い方がよくわからない…
PyTorchを使用するご利益が知りたい！

この悩みを徹底的に解決します。

PyTorchの理解を苦しめる理由の一つとして、そもそも実装するモデルが難しすぎるという説があります（例えば、深層学習や畳み込みニューラルネットワークから始まったり…）

そこで、本記事では最も簡単なモデルである線形回帰（単回帰）を具体例にPyTorchの使い方を説明します。

また、PyTorchを使用するご利益を理解するために、PyTorchで利用できるフレームワークを使用せずに実装を行います。

そして、徐々にPyTorchのフレームワークを使用していき、ご利益を感じることができるように工夫しました。

『こんな簡単なモデルで練習しても意味あるのかよ…』と思う方もいると思います。

結論、めちゃめちゃ意味あります。

最後まで読み進めれば理解できると思いますが、どんなに複雑なモデルになっても本記事で紹介するコードの一部を変更するだけです！

実は、それがPyTorchを使用するご利益なのです。

PyTorchを使用するための準備
- 必要なライブラリをインポート
使用するデータとモデルについて
- 使用するデータについて
- 使用するモデルについて｜単回帰
PyTorchのフレームワークを使用せずに実装
PyTorchの自動微分を用いた実装
optimizerを使用
nn.Moduleを使用したモデル設計
まとめ

PyTorchを使用するための準備

Google Colaboratoryを使用する場合は、PyTorchは最初から使える状態になっています。

基本的には、GPUを無料で提供している『Google Colaboratory』がおすすめです。

インストール方法に関しては下記を参考にしてください。

【10分完了】Google Colaboratoryのインストール法・使い方Google Colabは、GPUを使用できるため、低コストかつ高速で機械学習の実装を行う際に必要不可欠なツールです。本記事では、Google Colabのインストール方法と注意事項を10〜15分程度でまとめました。...

仮にAnnaconda等を使用したい場合は、下記のコードでPyTorchを事前にインストールしてください。

pip3 install torch torchvision

必要なライブラリをインポート

まずは、使用するライブラリをインポートしてください。

import numpy as np
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.optim as optim

使用するデータとモデルについて

まずは、使用するデータとモデルについて説明します。

使用するデータについて

まずは、使用するデータについて説明します。

データの入力は、標準正規分布に従う乱数を用い、出力は$y = 3 x$にノイズを追加したものを使用します。

# 標準正規分布に従う入力
data = np.random.randn(200, 1)
# y=3xにノイズを追加した出力
label = 3*data + np.random.randn(200, 1)*0.5

訓練データとテストデータに分けましょう。

x_train = data[:150, :]
y_train = label[:150, :]
x_test = data[:50, :]
y_test = label[:50, :]

PyTorchを使用するためにTensorに変換しましょう（＊Pytorchを使用する際は、必ずfloat32を使用しましょう）

# tesnsor化 : float32に変更
x_train = torch.tensor(x_train).float()
y_train = torch.tensor(y_train).float()
x_test = torch.tensor(x_test).float()
y_test = torch.tensor(y_test).float()

使用するデータを可視化しておきましょう。

fig, ax = plt.subplots()
ax.scatter(x_train, y_train, alpha=0.8, label='train data')
ax.scatter(x_test, y_test, alpha=0.8, label='test data')
ax.set_xlabel(r'$x$', fontsize=20)
ax.set_ylabel(r'$y$', fontsize=20)
ax.legend()
plt.show()

<出力>

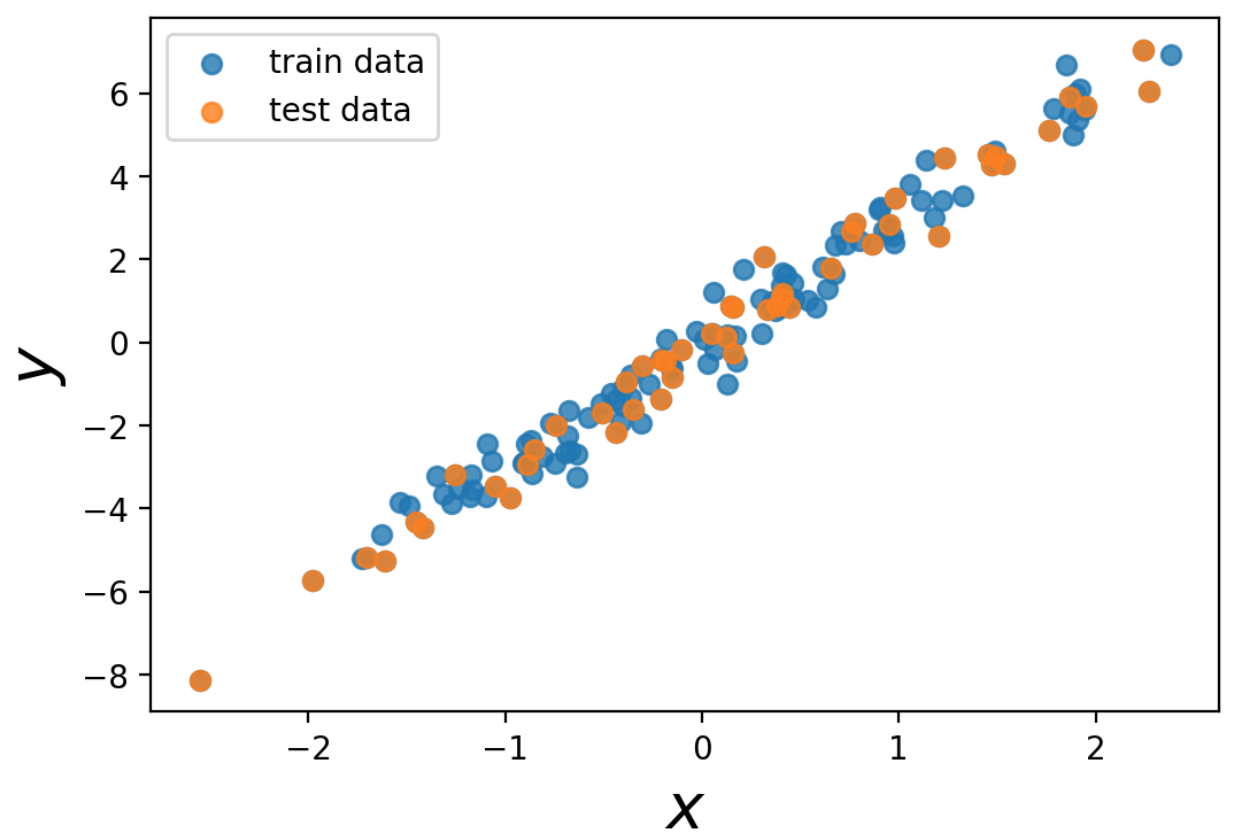
使用するモデルについて｜単回帰

使用するモデルは、以下の関数を使用します。

$$f(x) = w x + b$$

このようにパラメータに関して線形なモデルを用いて、データの入出力関係を表現する枠組みを『線形回帰』と言います

今回のモデルは線形回帰の中でも、特に『単回帰』と呼ばれています。

誤差関数としては、平均二乗誤差を最小化するようにパラメータを決定します。

$$L(w, b) = \frac{1}{N} \sum_{i=1}^{N} \left((w x_{i} + b) – y_{i} \right)^{2}$$

実は、最小化条件は簡単に求めることができます。

しかし、今回はPyTorchの使い方を学ぶために勾配降下法により数値的に最小化します。

そのために以下のように誤差関数の勾配を求めて、勾配降下法を使用します。

\begin{align} \frac{\partial L(w, b)}{\partial w} &= \frac{1}{N} \sum_{i=1}^{N} (2x_{i})((w x_{i} + b)) – y_{i}) \\ \frac{\partial L(w, b)}{\partial b} &= \frac{1}{N} \sum_{i=1}^{N} ((w x_{i} + b)) – y_{i}) \end{align}

PyTorchのフレームワークを使用せずに実装

まずは、PyTorchのフレームワークを一個も使用せずにPyTorchのTensorのみを使用して今回の単回帰を実装します。

まずは、モデル・損失関数・パラメータの初期値・学習率・エポック数を以下のように定義します。

# 学習モデルを定義
def model(x):
    return w*x + b

# 損失関数を定義
def criterion(output, y):
    loss = ((output - y)**2).mean()
    return loss

# パラメータの初期値
w = torch.tensor(0.0).float()
b = torch.tensor(0.0).float()

# 学習率
lr = 0.01

# エポック数
num_epoch = 1000

次に、先ほど計算した勾配を利用して、パラメータの学習を実行するコードを以下に示します。

train_loss_list = []
for epoch in range(num_epoch):
    # 予測
    output = model(x_train)
    # 損失関数を計算
    loss = criterion(output, y_train)
    # 勾配を計算
    grad_w = ((2*x_train)*(output-y_train)).mean()
    grad_b = (output-y_train).mean()
    # パラメータ更新
    w -= lr*grad_w
    b -= lr*grad_b
    grad = 0
    # lossを記録
    if (epoch%5==0):
        train_loss_list.append(loss)
        print(f'【EPOCH {epoch}】 loss : {loss:.5f}')

<出力>

【EPOCH 0】 loss : 9.74301
【EPOCH 5】 loss : 7.90484
【EPOCH 10】 loss : 6.42305
            :
            :
            :
【EPOCH 990】 loss : 0.22383
【EPOCH 995】 loss : 0.22383

損失関数の値と$w$と$b$の予測値を以下に示します。

fig, ax = plt.subplots()
epoch_list = np.arange(0, 1000, 5)
ax.plot(epoch_list, train_loss_list)
ax.set_title(f'Result : w = {w:.4f}, b = {b:.4f}', fontsize=15)
ax.set_ylabel('train loss', fontsize=20)
plt.show()

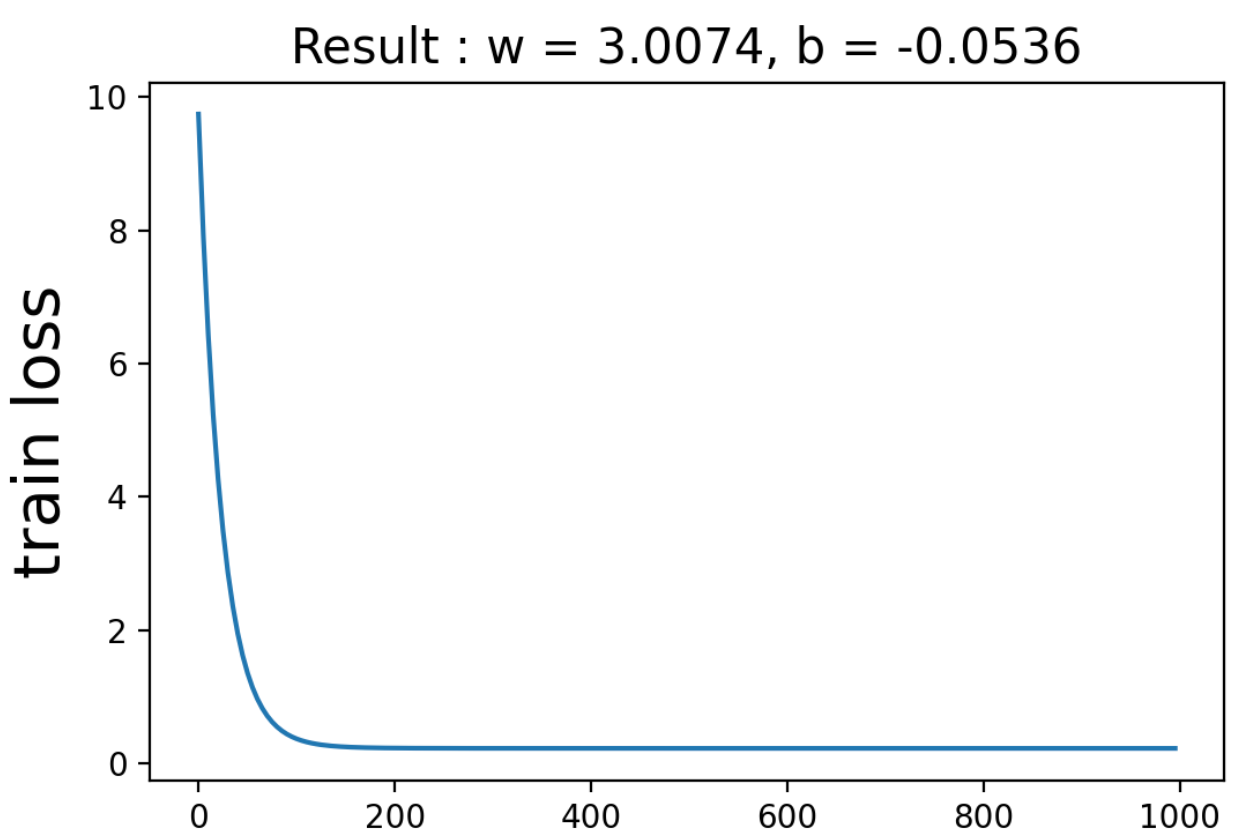
次にテストデータの出力と予測値を可視化します。

# 予測値
pred = model(x_test)

fig, ax =plt.subplots()
ax.scatter(x_test, y_test, c='orange', alpha=0.5, label='test data')
ax.scatter(x_test, pred, c='blue', alpha=0.5, label='prediction')
ax.set_xlabel(r'$x$', fontsize=20)
ax.set_ylabel(r'$y$', fontsize=20)
ax.legend()
plt.show()

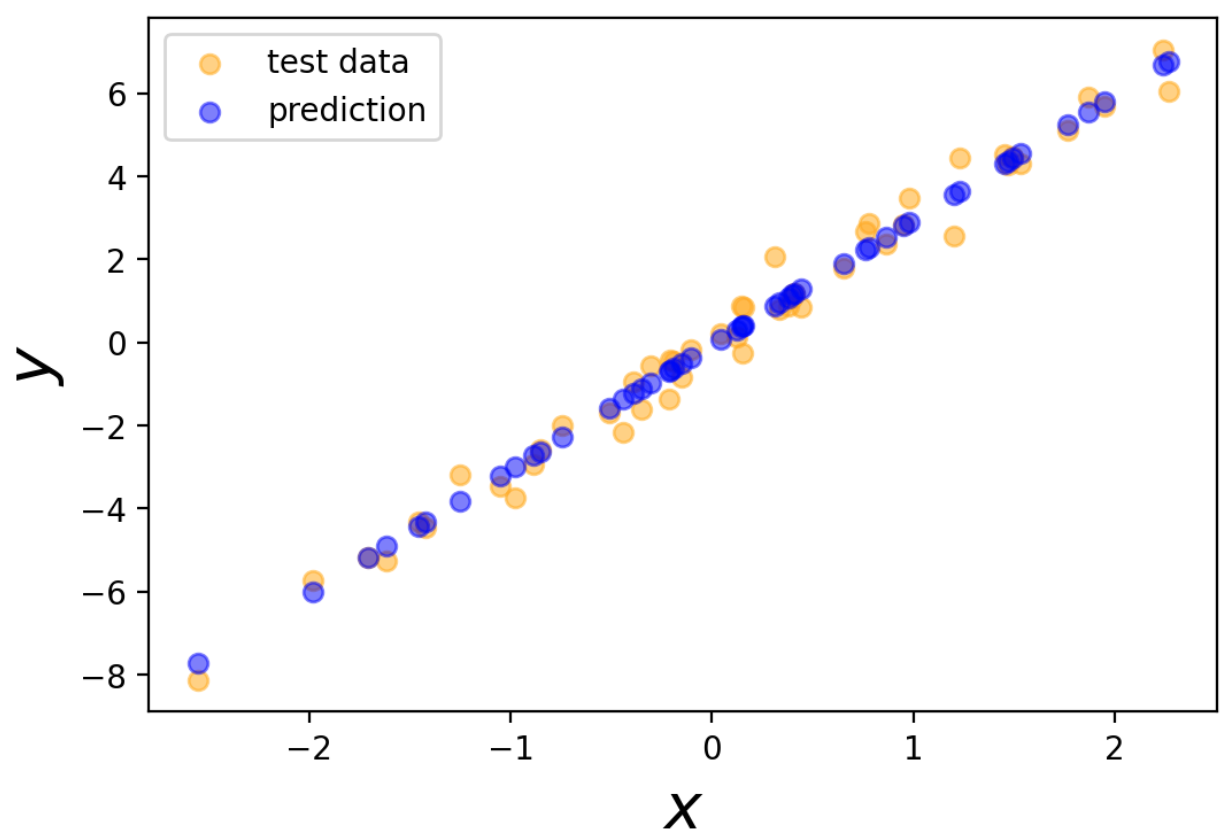
テストデータの出力をある程度再現できているのがわかります。

PyTorchの自動微分を用いた実装

さきほどの実装では、モデルが定義されたモデルごとに勾配を計算する必要がありました。

しかし、PyTorchの自動微分という機能を使用れば、モデルごとにわざわざ勾配を計算する必要がありません！

そこで、次は自動微分機能を使用した実装例を紹介します。

# 学習モデルを定義
def model(x):
    return w*x + b

# 損失関数を定義
def criterion(output, y):
    loss = ((output - y)**2).mean()
    return loss

# パラメータの初期値
w = torch.tensor(0.0, requires_grad=True).float()
b = torch.tensor(0.0, requires_grad=True).float()

# 学習率
lr = 0.01

# エポック数
num_epoch = 1000

微分したいパラメータのTensorを生成する際に『requires_grad=True』とすることで自動微分が可能となります。

学習部分のコードは以下のようになります。

train_loss_list = []
for epoch in range(num_epoch):
    # 予測
    output = model(x_train)
    # 損失関数を計算
    loss = criterion(output, y_train)
    # 勾配を計算
    loss.backward()

    with torch.no_grad():
        # パラメータ更新
        w -= lr*w.grad
        b -= lr*b.grad
        # 勾配の初期化
        w.grad.zero_()
        b.grad.zero_()

    # lossを記録
    if (epoch%5==0):
        train_loss_list.append(loss)
        print(f'【EPOCH {epoch}】 loss : {loss:.5f}')

先ほど同じ結果が得られると思います！

なんと『loss.backward()』とするだけで、簡単に勾配が計算できるのです。

＊素朴に勾配を使用する場合は、『with torch.no_grad():』のブロック内にパラメータ更新のコードを書いてください。

一応予測値も同じ結果が返ってくることも確認しておきます。

fig, ax = plt.subplots(dpi=200)
epoch_list = np.arange(0, 1000, 5)
ax.plot(epoch_list, train_loss_list)
ax.set_title(f'Result : w = {w:.4f}, b = {b:.4f}', fontsize=15)
ax.set_ylabel('train loss', fontsize=20)
plt.show()

<出力>

同じ結果が得られたことがわかりますね。

optimizerを使用

毎回毎回、勾配更新のコードを実装するのは大変ですね…

しかし、PyTorchのOptimizerという機能を使用することで、どんなモデルに対しても、パラメータ更新部分を１行で実装できます。

また、PyTorchでは、有名どころの誤差関数は搭載されており、1から実装する必要はありません。

まずは、optimizerとnn.MSELoss()（平均二乗誤差）を使用して初期設定を定義します。

# 学習モデルを定義
def model(x):
    return w*x + b

# パラメータの初期値
w = torch.tensor(0.0, requires_grad=True).float()
b = torch.tensor(0.0, requires_grad=True).float()

# 損失関数を定義
criterion = nn.MSELoss()

# 最適化手法を指定
optimizer = optim.SGD([w, b], lr=0.01)

# エポック数
num_epoch = 1000

学習のコードは以下のようになります。

train_loss_list = []
for epoch in range(num_epoch):
    # 勾配初期化
    optimizer.zero_grad()
    # 予測
    output = model(x_train)
    # 損失関数を計算
    loss = criterion(output, y_train)
    # 勾配を計算
    loss.backward()
    # パラメータ更新
    optimizer.step()

    # lossを記録
    if (epoch%5==0):
        train_loss_list.append(loss.detach().item())
        print(f'【EPOCH {epoch}】 loss : {loss:.5f}')

パラメータ更新の部分が、『optimizer.step()』という１行で書くことができました！

一応、同じ結果が得られているか確認しておきます。

fig, ax = plt.subplots(dpi=200)
epoch_list = np.arange(0, 1000, 5)
ax.plot(epoch_list, train_loss_list)
ax.set_title(f'Result : w = {w:.4f}, b = {b:.4f}', fontsize=15)
ax.set_ylabel('train loss', fontsize=20)
plt.show()

<出力>

同じ結果が得られましたね。

nn.Moduleを使用したモデル設計

深層学習は、今回使用した線形回帰のようなネットワークが層状に積み重なったものと見なすことができます。

では、仮に1000層のネットワークを構築したい考えます。

その時にこれまでと同様に1からモデルを実装したら途方もない時間がかかってしまいます…

しかし、PyTorchは、深層学習を構成する線形回帰のようなネットワークや様々な変換を一つのブロックと見なして、それを積み重ねることで簡単にネットワークが作成できます。

その場合は、nnモジュールを使用します。

具体的には以下のようにネットワークを構築します。

# 学習モデルを定義
class Net(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc = nn.Linear(1, 1, bias=True)

        # 初期値の設定   
        nn.init.constant_(self.fc.weight, 0.0)
        nn.init.constant_(self.fc.bias, 0.0)
        
    def forward(self, x):
        x = self.fc(x)
        return x

# インスタンス生成
model = Net()

# 損失関数を定義
criterion = nn.MSELoss()

# 最適化手法を決定
optimizer = optim.SGD(model.parameters(), lr=0.01)

# エポック数
num_epoch = 1000

詳しい使い方は下記を参考にしてください（実は、nn.linearを使わなくても自分で一から作ることもできます！）

PyTorchのネットワークの書き方を徹底解説｜カスタムレイヤー作成も説明！Pytorchのネットワークの書き方を二つ説明しました。一つ目はSequentialを使用する方法で、二つ目はネットワークを自作モジュール化する方法を説明しました。また、二つのメリット・デメリットを具体例を通じて理解できるように工夫しました。...

学習のコードは変わらず以下のようになります。

train_loss_list = []
for epoch in range(num_epoch):
    # 訓練モードに変更
    model.train()
    # 勾配初期化
    optimizer.zero_grad()
    # 予測
    output = model(x_train)
    # 損失関数を計算
    loss = criterion(output, y_train)
    # 勾配を計算
    loss.backward()
    # パラメータ更新
    optimizer.step()

    # lossを記録
    if (epoch%5==0):
        train_loss_list.append(loss.detach().item())
        print(f'【EPOCH {epoch}】 loss : {loss.detach().item():.5f}')

確認のため誤差関数とパラメータの推定値を表示します。

fig, ax = plt.subplots()
epoch_list = np.arange(0, 1000, 5)
ax.plot(epoch_list, train_loss_list)
# w, bの確認の仕方が異なることに注意
ax.set_title(f'Result : w = {model.fc.weight.item():.4f}, b = {model.fc.bias.item():.4f}',
             fontsize=15)
ax.set_ylabel('train loss', fontsize=20)
plt.show()

<出力>

同じ結果が得られました！

実は、モデルが複雑になっても変わる部分は、学習モデルの定義の部分だけなんです。

そのため、ここで学習したプロセスを利用すれば、どんな複雑なモデルに対しても適用できます。