Pythonでエラーバー（誤差棒）付きのグラフを作ってみた

本記事では、Pythonのmatplotlibを用いてエラーバー（誤差棒）付きのグラフの作成方法を解説します。

本記事の内容

エラーバー（誤差棒）の基本
Pythonでエラーバー（誤差棒）つきのグラフを作成
Pythonで３種類のエラーバーつきグラフを作成

本記事を読むメリット

初心者の方でもエラーバーつきグラフが作成できるようになる
エラーバーについて知ることができる
エラーバーの違いを視覚的に見ることができる

エラーバー（誤差棒）の基本
- エラーバー（誤差棒）とは
Pythonでエラーバー（誤差棒）つきのグラフを作成
- 必要なライブラリをインストール
- matplotlibのerrorbarの使い方
Pythonで３種類のエラーバー（誤差棒）つきグラフを作成
参考資料
- 参考文献
- 参考URL
まとめ

エラーバー（誤差棒）の基本

まずは、エラーバー（誤差棒）の意味を簡単に説明していきます。

＊すでにエラーバーについてご存知の方は読み飛ばしてください。

Wikipediaでは、以下のようにエラーバーを説明しています。

エラーバーは測定がどれほど正確か、逆にいえば、真の値が報告された値かたどれほど離れているかの概念を与える。エラーバーはしばしば、不確かさの標準偏差、標準誤差、あるいは任意の信頼区間（例えば95%信頼区間）を表わす。これらの量は同じではないため、グラフあるいは説明文にはエラーバーが何を表わしているかを明確に記さなければならない。

引用 : Wikipedia

だいたいこの説明で理解できると思いますがもう少し掘り下げていきます。

エラーバー（誤差棒）とは

エラーバー（誤差棒）とはWikipediaの説明にあるように、データのばらつき具合を表しています。

しかし、抽象的にばらつき具合と言っても、『ばらつき』の概念は一意に決まらないため、エラーバー（誤差棒）が示す『ばらつき』を明示的に示す必要があります。

具体的にばらつきの指標としては以下のようなものがあります。

ばらつきの指標
データの区間	一般には使用しない（データの範囲が知りたいときに使用）
標準偏差（SD）	母集団のばらつき具合を知りたいとき
標準誤差（SE）	平均値（期待値）の精度が知りたいとき（誤差の乗り方がガウス分布だと仮定したときの標準偏差）
信頼区間	母集団のパラーメータを一定確率で含む範囲

このように、ばらつきを表す指標というのは複数存在するため、エラーバー（誤差棒）を使用するときは、どの指標を使用しているのかを明示する必要があります。

信頼区間を使用する場合は、何%なのかを示す必要もあります。

Pythonでエラーバー（誤差棒）つきのグラフを作成

ここからは、Pythonのmatplotlibというライブラリを利用して、エラーバー（誤差棒）つきのグラフを作成していきます。

この章の目標は、とりあえずエラーバー（誤差棒）がついているグラフを作成することです！

matplotlibの使い方に慣れていない方は下記を参考にしてください。

【15分】Pythonでグラフを作成する方法｜matplotlibの基本をマスターPythonでグラフを書くことが難しそうだと思っていませんか？実は、Pythonを使用したグラフ作成は、excelより便利で簡単です。この記事では、初心者でもグラフが書けるように丁寧にpythonのグラフの作成法を説明します。...

必要なライブラリをインストール

まずは、必要なライブラリをインストールしていきます。

下記のコードを実行してください。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

Pandasをインポートする必要は本来ありませんが、綺麗に表を作成するために今回はインポートしました。

＊使い方を知らなくても本記事を読み進めることは可能です。

Pandasの基本的な使い方に関しては下記を参考にしてください。

【入門】pandasの使い方｜基本的な使い方を20分で攻略！『pandasを使ってみたいけど何から手をつけて良いかわからない...』という方のために本記事を作成しました。本記事では、Pandasを利用したデータ解析に必要不可欠なものだけをまとめました。...

matplotlibのerrorbarの使い方

今回、エラーバー（誤差棒）ありのグラフを作成するために、matplotlibのerrorbarメソッドを使用します。

具体的にエラーバー（誤差棒）付きのグラフのコードを示した方がわかりやすいと思うので、今回は、誤差の値を以下のように適当に決め、とりあえず誤差棒ありのグラフを書いてみます。

# 誤差の値
xerr = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6])
yerr = np.array([0.6, 0.5, 0.4, 0.3, 0.2, 0.1])

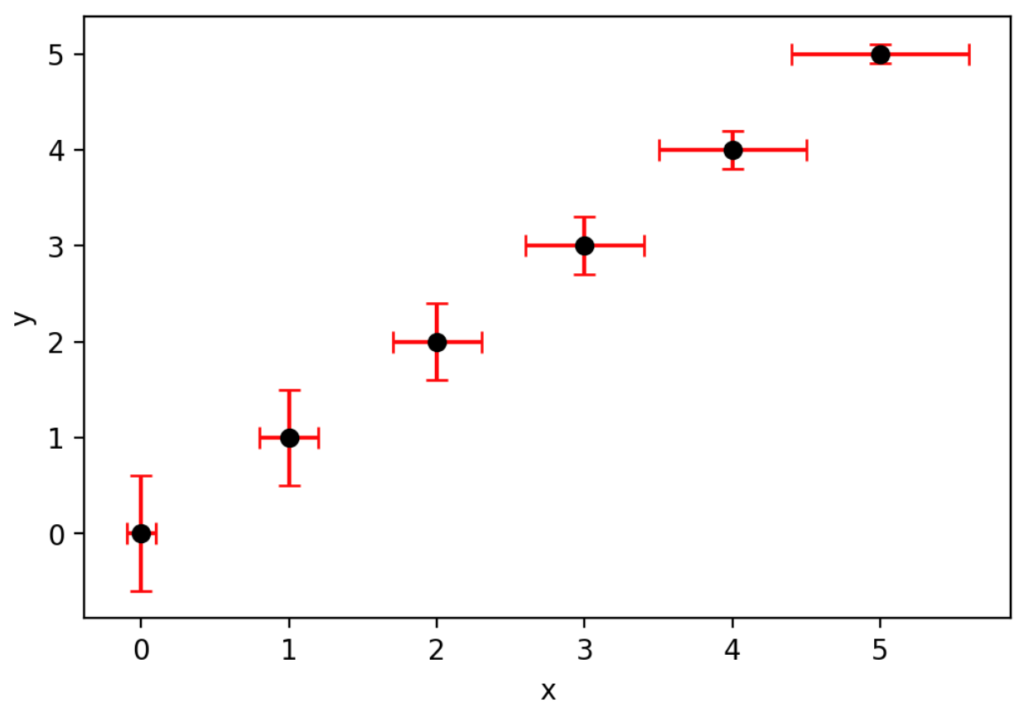
エラーバー（誤差棒）つきグラフのコードを以下に示します。

fig, ax = plt.subplots()
ax.errorbar(x, y, xerr=xerr, yerr=yerr, capsize=4, fmt='o', ecolor='red', color='black')
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()

引数について以下に簡単にまとめます。

errorbarメソッド
x	x軸の値
y	y軸の値
xerr	x軸の各値に対する誤差
yerr	y軸の各値に対する誤差
ecolor	エラーバー（誤差棒）の色
elinewidth	エラーバー（誤差棒）の線の太さ
capsize	エラーバー（誤差棒）の横線の長さ
fmt	データ点のマーカーの種類, ‘none’とするとエラーバーのみ表示される

＊通常のmarkerに対するキーワード引数も利用できる。

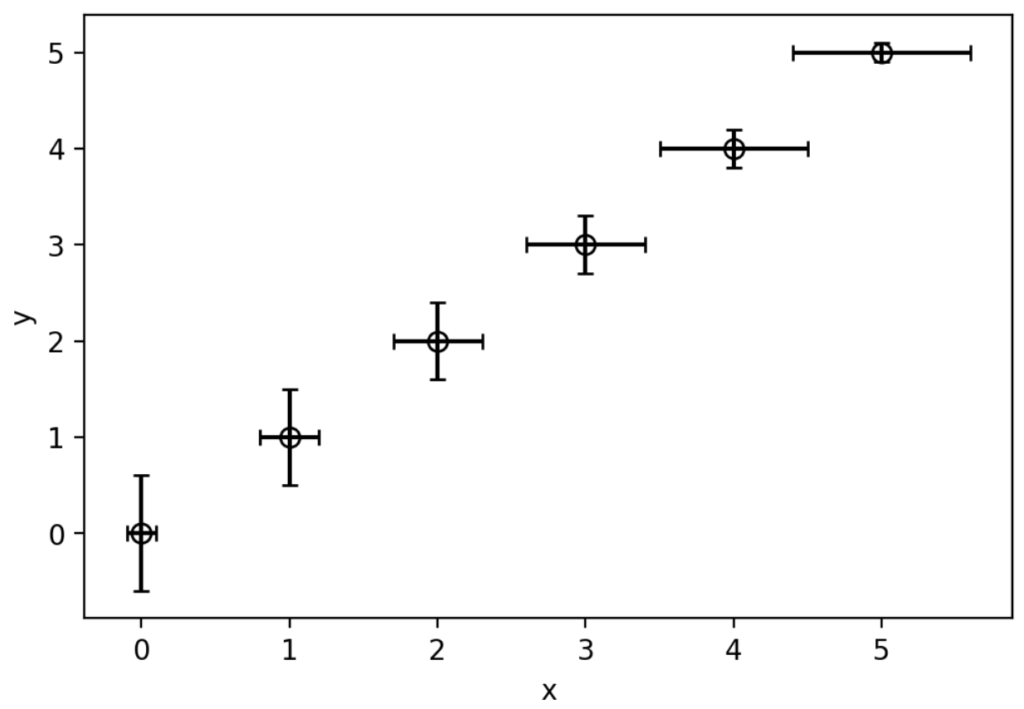
さらに通常のmarkerに対するキーワード引数も用いて最もオーソドックスな誤差棒付きグラフを以下に示しておきます。

fig, ax = plt.subplots()
# ms : マーカーサイズ, mfc : マーカーのファイスカラー, mec : マーカーのエッジカラー
ax.errorbar(x, y, yerr=yerr, xerr=xerr, capsize=3, fmt='o', ecolor='k', ms=7, mfc='None', mec='k')
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()

ここからは、具体的に作成したデータをもとに3種類のエラーバー（誤差棒）付きグラフを作成していきます。

Pythonで３種類のエラーバー（誤差棒）つきグラフを作成

ここからは、実際に範囲・標準偏差・標準誤差をエラーバーとするグラフを作成していきます。

これまで使用していたサンプルを使用し、以下の順番で説明していきます。

範囲をエラーバーとしたグラフ
標準偏差をエラーバーとしたグラフ
標準誤差をエラーバーとしたグラフ

では、詳しく説明していきます。

サンプルデータの作成

今回使用するサンプルデータを作成していきます。

まずは、観測者が未知の真の値を作成していきます。

# 真の値(観測者は未知)
x = np.array([0, 1, 2, 3, 4, 5])
y = x

これらを図示すると以下のようになります。

fig, ax = plt.subplots()
ax.plot(x, y, marker='o')
ax.set_xlabel('x')
ax.set_ylabel('y_pop')
plt.show()

yを真の値（母平均）とし、xを観測した位置だと思ってください。

実際の観測では、測定誤差等が生じてしまうため、直接真の値を知ることはできません。

今回は、仮想的に観測を再現するために、各位置で10回の観測を行い、各観測点は正規分布によるノイズを含むという設定を考えます。

具体的には下記のコードで仮想的な観測を行うことができます。

y_obs = np.zeros((10, 6))
for i in range(10):
    y_obs[i, 0] = x[0] + (np.random.rand()-0.3)*2.0
    y_obs[i, 1] = x[1] + (np.random.rand()-0.3)*2.0
    y_obs[i, 2] = x[2] + (np.random.rand()-0.3)*2.0
    y_obs[i, 3] = x[3] + (np.random.rand()-0.3)*2.0
    y_obs[i, 4] = x[4] + (np.random.rand()-0.3)*2.0
    y_obs[i, 5] = x[5] + (np.random.rand()-0.3)*2.0

data = pd.DataFrame(y_obs, index=[f'観測値{i}' for i in range(1, 11)])
data

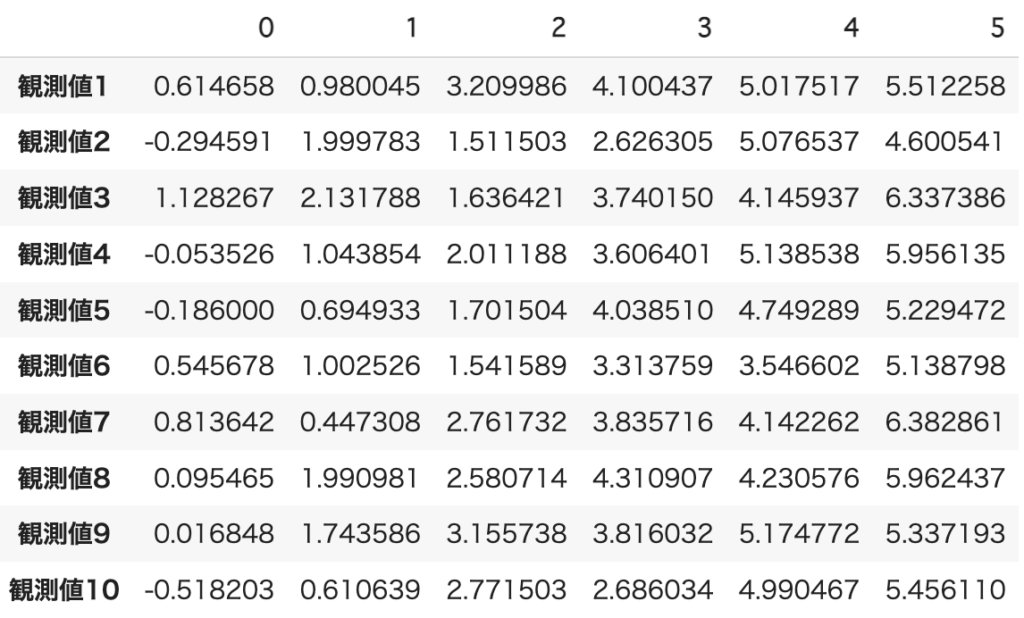
これで、サンプルデータの作成は完成です。

範囲をエラーバーとしたグラフ

まずは、範囲をエラーバーとしたグラフを書いていきます。

PandasのDataFrameを使用したおかげで、統計量を簡単に計算することができます。

下記のコードで各位置に対する観測値の範囲を計算することできます。

# データの範囲
yerr_scope = np.array(data.max() - data.min())
print(yerr_scope)

[1.64647011 1.68448025 1.69848303 1.68460175 1.62817027 1.78231986]

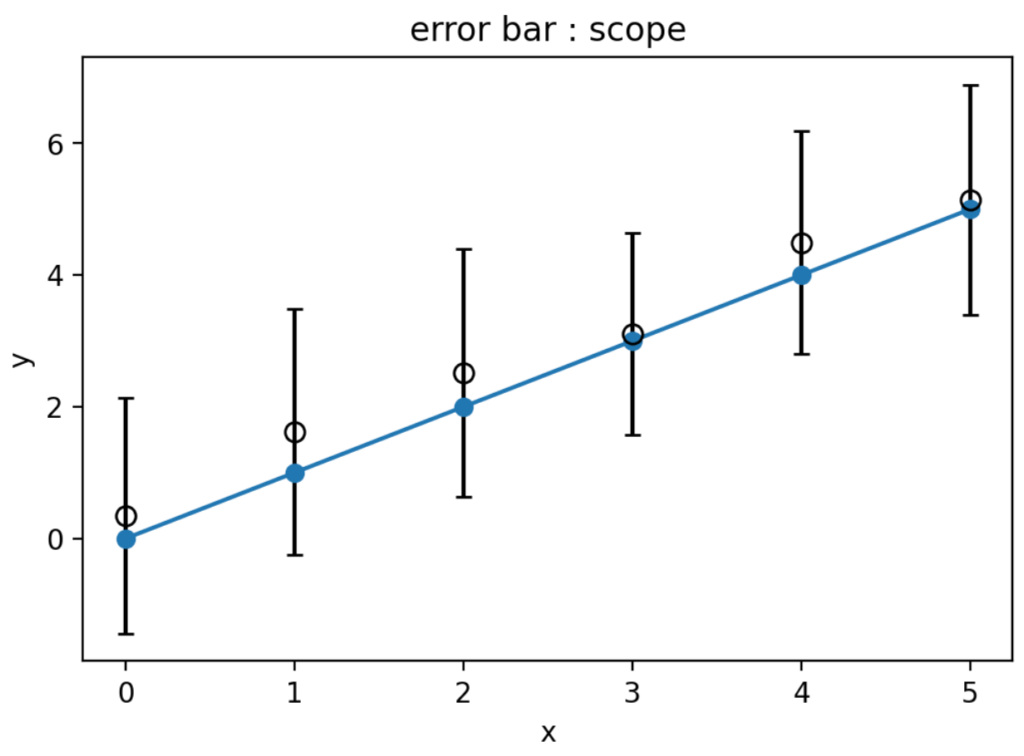
この値を使って範囲のエラーバーつきのグラフを作成していきます。

# 各点を平均値とする
y_mean = np.array(data.mean())

fig, ax = plt.subplots()
ax.plot(x, y, marker='o')
ax.errorbar(x, y_mean, yerr=yerr_scope, capsize=3, fmt='o', ecolor='k', ms=7, mfc='None', mec='k')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('error bar : scope')
plt.show()

標準偏差をエラーバーとしたグラフ

次に標準偏差をエラーバーとしたグラフを作成していきます。

まずは、各位置の標準偏差を求めます。

# 標準偏差
yerr_sd = np.array(data.std()) 
print(yerr_sd)

[0.64367857 0.65151205 0.70707588 0.61404578 0.39999493 0.62760875]

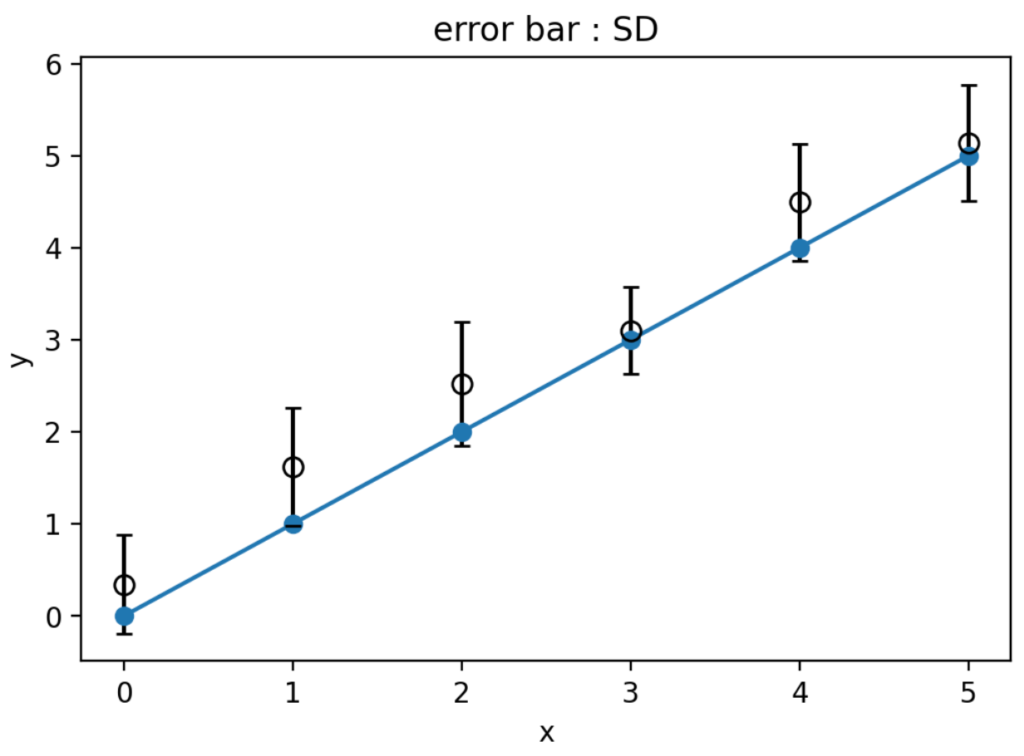
この値を使ってエラーバーつきのグラフを作成します。

# 各点を平均値とする
y_mean = np.array(data.mean())

fig, ax = plt.subplots()
ax.plot(x, y, marker='o')
ax.errorbar(x, y_mean, yerr=yerr_sd, capsize=3, fmt='o', ecolor='k', ms=7, mfc='None', mec='k')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('error bar : SD')
plt.show()

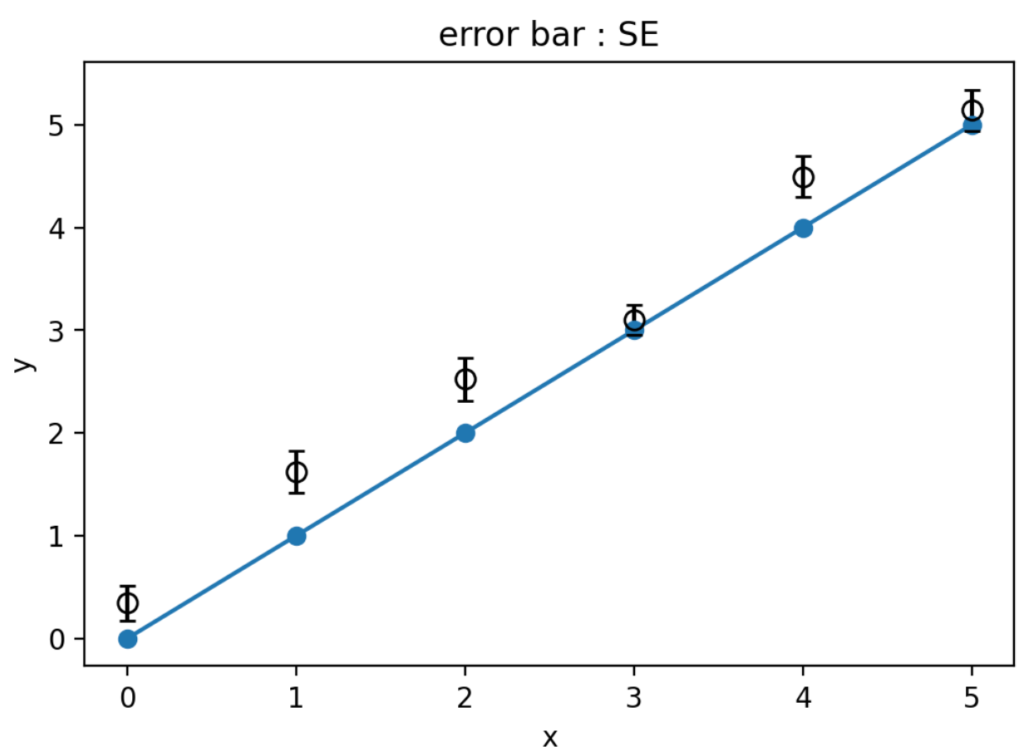
標準誤差をエラーバーとしたグラフ

最後に標準誤差をエラーバーとしたグラフを描画していきます。

同様に、標準誤差を求めます。

# 標準誤差
yerr_se = np.array(data.std() / np.sqrt(len(data)))
print(yerr_se)

[0.20354904 0.2060262  0.22359703 0.19417832 0.1264895  0.19846731]

標準誤差は以下のように求めることができるので、標準偏差を使用し求めました。

$$\text{SE} = \frac{\text{SD}}{\sqrt{N}}$$

ここで、Nは観測回数（観測サンプル数）を表します。

これらの値を使ってグラフを描画します。

# 各点を平均値とする
y_mean = np.array(data.mean())

fig, ax = plt.subplots()
ax.plot(x, y, marker='o')
ax.errorbar(x, y_mean, yerr=yerr_se, capsize=3, fmt='o', ecolor='k', ms=7, mfc='None', mec='k')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('error bar : SE')
plt.show()