本ブログで使用する数学記法
本ブログで使用する数学記法を説明します。
本ブログで使用する数学記法
| \( \mathbb{R} \) | 実数集合 |
|---|---|
| \( \mathbb{R}_{+} \) | 非負の実数集合 |
| \( x \) | 確率変数の実現値 |
| \( {\bf x} \) |
ベクトル \( {\bf x} = (x_{1}, x_{2}, x_{3}, \ldots, x_{n} )^{\text{T}} \) 特に断りがなければ、列ベクトルを利用する。 各要素を\(\{\mathbf{x}\}_{i} = x_{i}\)と表記する。 |
| \( X \) | 確率変数 |
| \( {\bf X } \) |
行列 より簡潔に、\({\bf X} = [x_{ij}]\)と表される。 各要素\(\{\mathbf{X}\}_{ij} = x_{ij} \)と表す。 |
| \( {\bf I} \) | 単位行列 |
| \( \text{det} {\bf X} \) | 行列式 |
| \({\bf 1}\)[A] | 定義関数 : Aが真のとき1、Aが偽のとき0 |
| \(\text{sign}(x) \) | 符号関数 : \(1~ (x \ge 0 ),~ -1~ (x < 0 ) \) |
| \(\| \cdot \| \) | 2- ノルム |
本ブログで使用する関数の記法について
| \(\sigma(x) \) |
ジグモイド関数 \(\sigma(x) = \frac{1}{1+e^{-x}} \) |
|---|---|
| \( \delta(x) \) |
デルタ関数 \( \int_{-\infty}^{\infty} f(x) \delta(x) dx = f(0) \) |
| \( \delta_{ij} \) |
クロネッカーのデルタ \(\delta_{ij} = \begin{cases} 1 & (i=j) \\ 0 & (i \neq j) \end{cases} \) |
| 項目名 | ここに説明文を入力してください。 |
| 項目名 | ここに説明文を入力してください。 |
オーダー記法について
| \(f = \mathcal{O}(g) \) | \( \exists \alpha \in \mathbb{R}_{+}~~ \exists x_{0} \in \mathbb{R}~~\forall x > x_{0}~~f(x) \le \alpha g(x) \) |
|---|---|
| \(f = o(g) \) | \( \forall \alpha > 0~~ \exists x_{0} \in \mathbb{R}~~\forall x > x_{0}~~f(x) \le \alpha g(x) \) |
| \(f = \Omega(g) \) | \( \exists \alpha \in \mathbb{R}_{+}~~ \exists x_{0} \in \mathbb{R}~~\forall x > x_{0}~~f(x) \ge \alpha g(x) \) |
| \(f = \omega(g) \) | \( \forall \alpha > 0~~ \exists x_{0} \in \mathbb{R}~~\forall x > x_{0}~~f(x) \ge \alpha g(x) \) |
論理式で目が追えなくなる人が多いと思うので、\(f = \mathcal{O}(g) \)を図を用いて解説します。
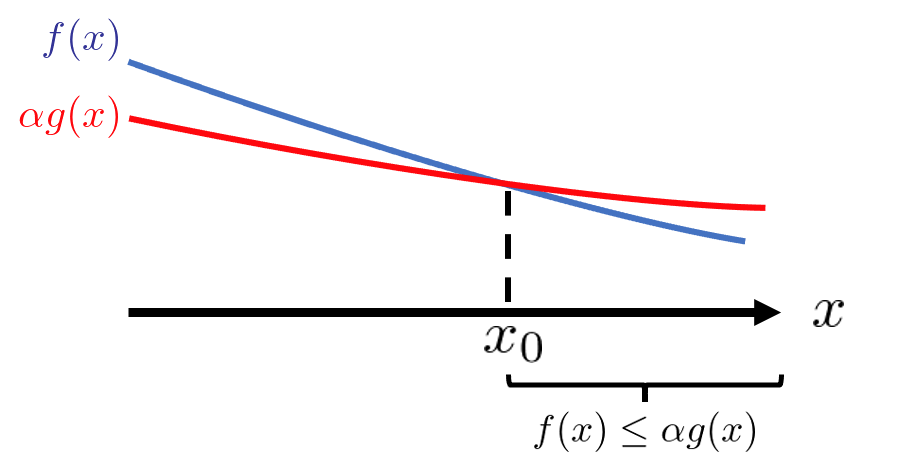
論理式を図で書くと上記のようになります。
つまり、\(x\)を大きくしていけば、いずれ、\(f(x)\)は\(\alpha g(x)\)よりも小さくなることを意味しています。
他のオーダ記法も同様の考え方で理解できます。
論理式の扱いに慣れるために
多くの方が苦手な、『ε- δ論法』的な説明をすんなり理解するために、『数学ガール』で利用されている記述を共有いたします。
具体例として、連続の定義を論理式で表現します。
関数\(f(x)\)が次式を満たすとき、\( f(x) \)は\(x=a\)で連続である。
$$\forall \epsilon > 0~, \exists \delta > 0, \text{s.t.}~ |x-a| < \delta \Rightarrow | f(x) – f(a) | < \epsilon$$
数学ガールの結城さんは、以下のようにわかりやすく解剖しています(1)。
\( \forall \epsilon > 0 \) : どんな正の数\(\epsilon\)に対しても
\(\exists \delta > 0 \) : \( \epsilon \)ごとに、\( \delta \)を適切に選べば
\( \text{s.t.} \) 〜 : 〜という条件を成り立たせることができる
引用元 : 数学ガール











